Radarbruk og ARPA
Forklaring av begreper
| ARPA | Automatic Radar Plotting Aid. Dette systemet viser vektorer og vektorinformasjon når et fartøy plottes. De første radar-anleggene hadde ikke ARPA, og derfor måtte man utlede disse vektorene manuelt på et plotteark. |
| Relativ vektor | Denne vektoren viser et fartøys relative bevegelse i forhold til eget fartøy. Denne vektoren finner radaren ved å ta flere peilinger og avstander til et mål. |
| Sann vektor | Forteller oss et objekts sanne bevegelse. Eget fartøys sanne vektor får radaren gjennom farts- og kursinformasjon fra instrumenter som er tilkoblet radaren. Fartøy over 10 000 BRT er det krav om godkjent ARPA-anlegg med logget fart gjennom vannet og kurs fra gyro eller andre godkjente kompassystemer. En del fartøy bruker fart over grunnen (Speed Over Ground) og kurs over grunnen (Course over Ground) fra satellittsystemer. |
| CPA | Closest Point of Approach eller nærmeste passeringspunkt på norsk. CPA sier noe om hvor nært eget fartøy vil komme et annet fartøy. |
| TCPA | Time to Closest Point of Approach sier noe om hvor lang tid det vil ta til et fartøy befinner seg på nærmeste passeringspunkt. Denne tiden vil telle ned og vises som minustid når fartøyet har passert det nærmeste passeringspunktet. |
| BCR | Bow Cross Range. Begrepet sier hvor nært et målfartøyet vil være eget fartøy når målfartøyet befinner seg rett forut. |
| BCRT | Bow Cross Range Time. Forteller oss hvor lang tid det vil ta før målfartøyet krysser rett forut. |
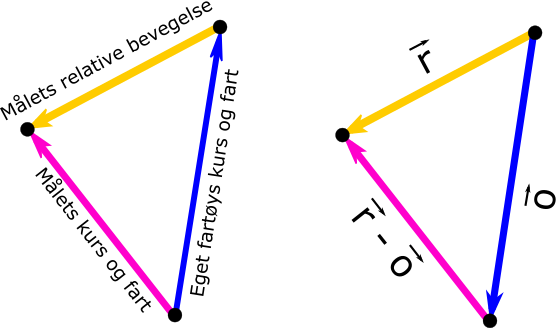
For å kunne forstå sjøveisreglene og tolke informasjon fra en ARPA-radar, må vi kjenne til begrepene vektor og vektortrekanten. En vektor er et retningsorientert linjestykke med en bestemt lengde formet som en pil med start- og sluttkoordinater. En vektor blir brukt til å beskrive en fysisk kvantitet, som fart eller kraft, som både har en størrelse og en retning. I navigasjon brukes blant annet vektor til å beskrive et skips retning (000° til 360°) og fart/distanse (nautiske mil) i et todimensjonalt plan.
En vektortrekant består av tre sider, der en radar vil finne målets relative bevegelse og presentere dette som målfartøyets relative vektor eller ekkobevegelse. En relativ vektor er summen av eget skips vektor og målfartøyets vektor. Trekker man fra eget skip vektor fra relativ vektor, vil man stå igjen med målfartøyets sanne vektor. Figur 9 viser sammenhengen mellom de ulike vektorene i vektortrekanten.
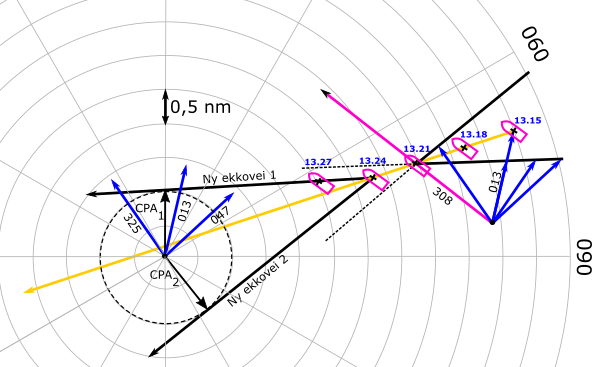
Figur 10 viser de ulike vektorene presentert i en tilfeldig trafikksituasjon mellom to fartøyer. Gul vektor viser målfartøyets ekkovei eller relative vektor og blå vektor (kurs 013˚) viser eget fartøys sanne vektor. Man kan da utlede målfartøyets sanne vektor som vist med rosa farge. Denne vektoren består av fartøyets kurs og fart. Kursen til målfartøyet er i dette tilfellet 308˚ og farten rundt 15 knop. I dette tilfellet har man flyttet et plott tre minutter frem fra kl. 13.21 til 13.24 for å gjøre en kurs- eller fartsforandring for å oppnå en ønsket CPA. Dette plottet er flyttet frem for å gi oss tid til å lage en ny fartstrekant. Den nye ekkoveien (svart strek) er parallelt forskjøvet tilbake i plott for kl. 13.21. Årsaken til at vi gjør dette er for å bruke opp igjen den sanne vektoren til målfartøyet. Vi kan da slå vår vektor bort på den nye ekkoveien. Dersom vi ønsker at fartøyet krysser foran oss med en CPA på 1 nautisk mil, må vi endre kurs til 047˚ og ønsker vi samme CPA når fartøyet passerer bak oss, må vi endre kurs babord til 325˚. Hvilken manøver som er mest aktuelt avhenger av om det er åpent farvann eller lukket farvann med hindringer. I de fleste tilfeller vil en manøver til styrbord i dette tilfellet være mest hensiktsmessig.
På en radar kan vektorlengden justeres, ved at man angir lengden på vektoren og dermed får informasjon om et skips bevegelse innen en gitt tid som man stiller inn selv. Det er ofte vanlig å bruke vektorer på 6 minutter i seilas i åpent farvann.
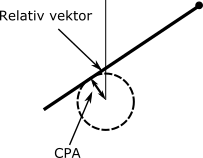
Dersom man skal vurdere nærmeste passeringsavstand, må man bruke relativ vektor. Relativ vektor for målfartøyet kan forlenges for å lettere vurdere om fartøyet vil passere foran eller aktenfor eget fartøy. Bruker man avstandsringer (Variable Range Marker, VRM) på radaren, kan man lettere måle og se endringer i et fartøys relative vektor. Dersom to fartøyers kurs har vært konstant over en lengre periode før en kollisjon, kan vi også utlede ekkoveien til fartøyene relativt til hverandre. Det vil derfor være relativt lett å avgjøre hvilke vikepliktsregler som eventuelt gjeldt etter del B avsnitt 2.
Sanne peilinger og relative peilinger
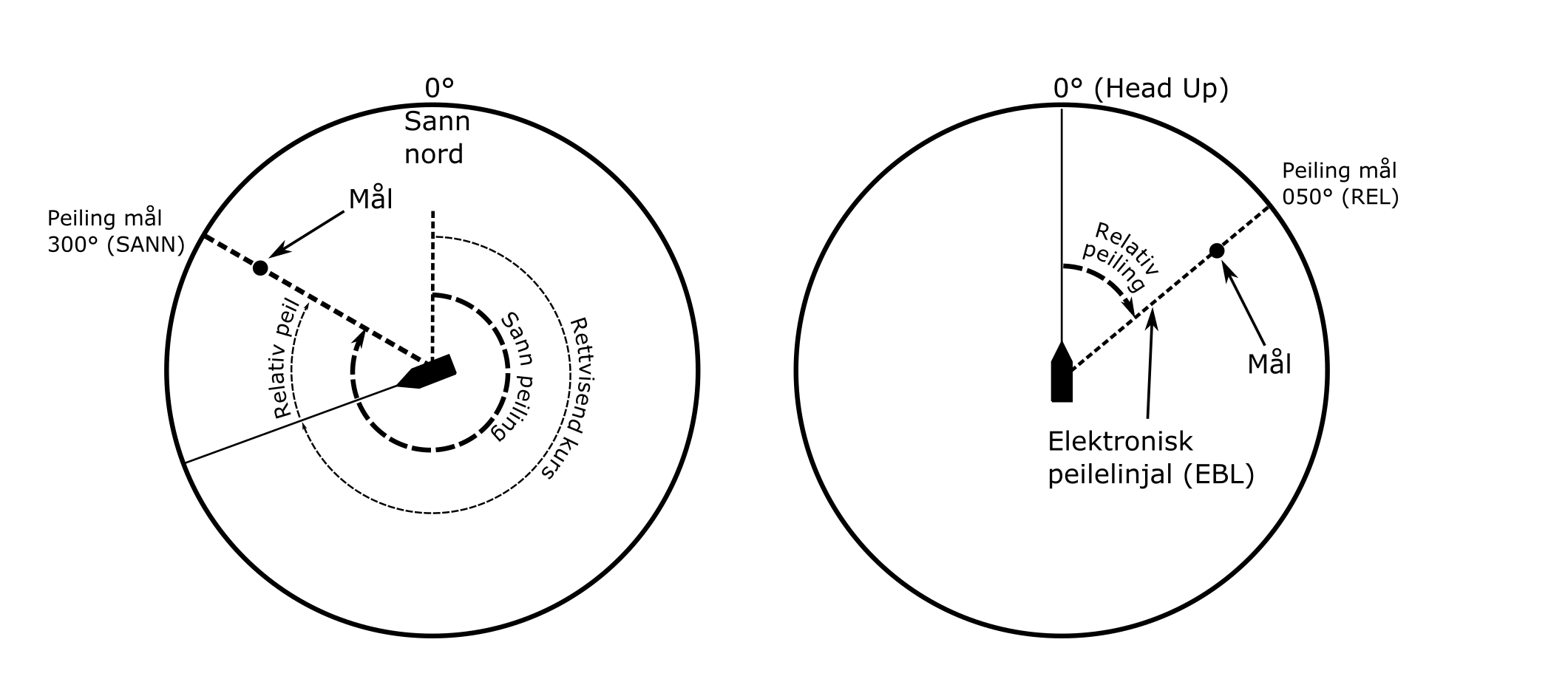
Det er viktig å kjenne til begrepene sanne peilinger og relative peilinger når man skal utlede vektorer eller oppgi en peiling på bro (se figur 12). En relativ peiling er peiling målt fra bauglinja og til målet. Dersom en radar står i Head Up, vil ofte peilingen vises som relative. En sann peiling kan utledes ved å legge fartøyets rettvisende kurs til den relative peilingen. Den sanne peilingen er da vinkelen på den buen som går fra sann nord til objektet.
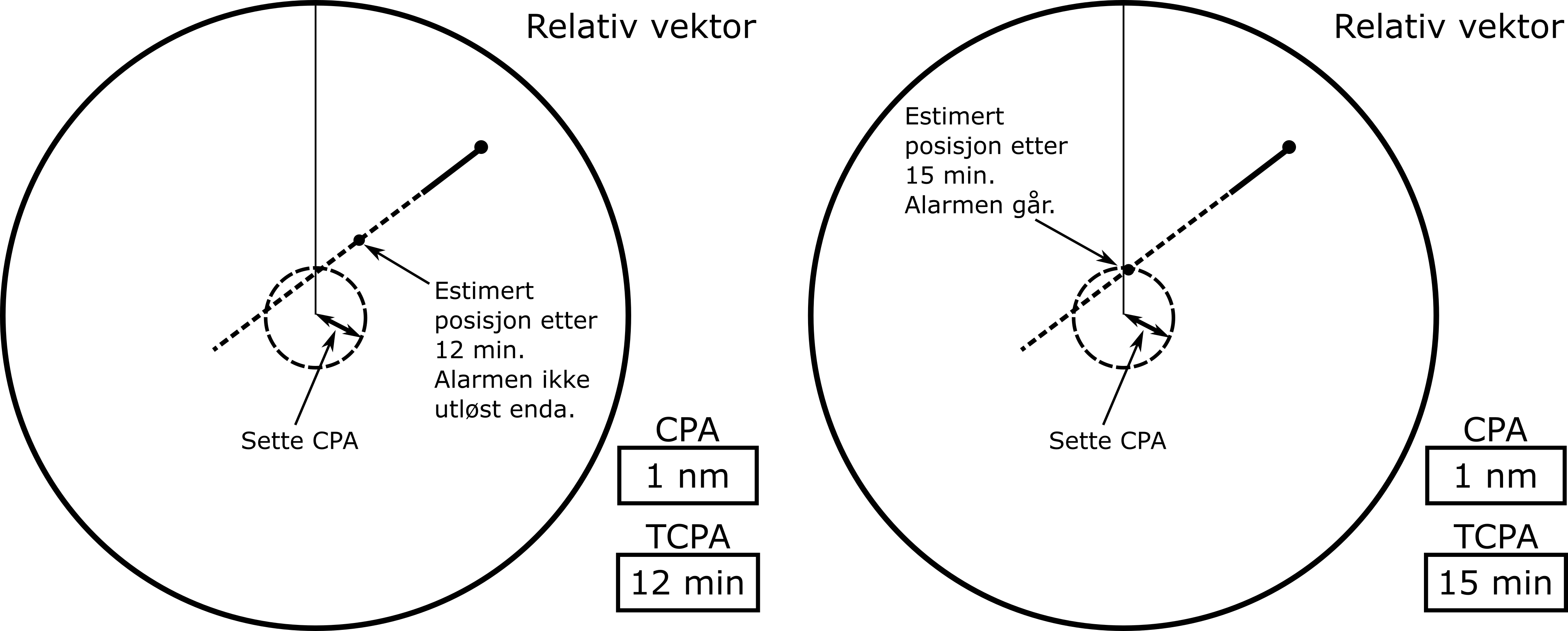
Det er viktig at alarmer for CPA, TCPA, BCR og BCRT blir stilt inn etter hvilket område skipet seiler. Seiler man i åpent farvann, kan gjerne alarmgrense for CPA og BCR settes til 2 nautiske mil, mens i trangt farvann kan det være aktuelt å redusere grensene til 1 nautisk mil. BCRT og TCPA kan typisk settes til 12 minutter i åpnet farvann og 6 minutter i trange farvann.
Det er viktig å huske på at det på noen fartøyer kan være en betydelig avstand fra radarantenna til baugen av fartøyet. Denne avstanden må tas med i vurderingen av CPA. En tidsgrense for begge alarmer (TCPA og BCT) kan stilles inn etter navigatørens ønsker. Med få båter i farvannet kan alarmen settes høyt, mens man i trangere farvann kan vurdere å redusere denne betydelig. Et eksempel på innstilling av alarmer vises i figur 13.
På de fleste radarer kan man sette inn «vaktområder» eller «guard Zones», der fartøyer plottes automatisk. Det må understrekes at slike guard zones ikke skal være en erstatning for manglende vakthold og utkikk.
Et spørsmål som mange stiller seg, er hva minste passeringsavstanden skal være for at man kan anta at det er fare for kollisjon. Det vil være helt klart at en CPA som er 0 nautiske mil vil utgjøre en fare for sammenstøt. Dette sammenfaller med regel 7, siden peilingen da ikke endrer seg. Når en fare for sammenstøt oppstår, vil være avhengig av hva som står i fartøyets sikkerhetsstyringssystem. Sier dette at man i åpent hav skal opprettholde en CPA på 1 nautisk mil, vil man kunne definere at en CPA som er mindre enn dette mulig utgjør en fare for sammenstøt. Dette kan også ses i sammenheng med at en CPA ofte vil være unøyaktig i starten ved plotting av mål på radaren eller dersom eget fartøy eller målfartøyet utfører en manøver.
Følgende tekst er hentet fra et sikkerhetsstyringssystem i et større internasjonalt driftsoperatørselskap:
«All (name of company) vessels should maintain a safe CPA in accordance with circumstances and conditions having due regard to the available sea room and proximity of navigational hazards.
As a guide at sea, a CPA of around one mile shall be maintained whenever conditions allow, and in accordance with the Regulation for Preventing Collision at Sea (COLREGS).
This guideline may be relaxed if OSV`s are in proximity of each other conducting joint manoeuvres or operations».
I dette rederiet er grensen for CPA satt til 1 nautisk mil, men en del rederi ønsker at offiserene skal opprettholde en CPA på 2 nautiske mil, spesielt gjelder det for passasjerskip og større skip med farlig last. Her vil også Bow Cross Range (BCR) være et viktig begrep. Dersom sikten reduseres bør man etterstrebe en høyere CPA, da man i all hovedsak må stole på det som presenteres på radaren. AIS kan være viktig hjelpemiddel, spesielt når sikten reduseres.
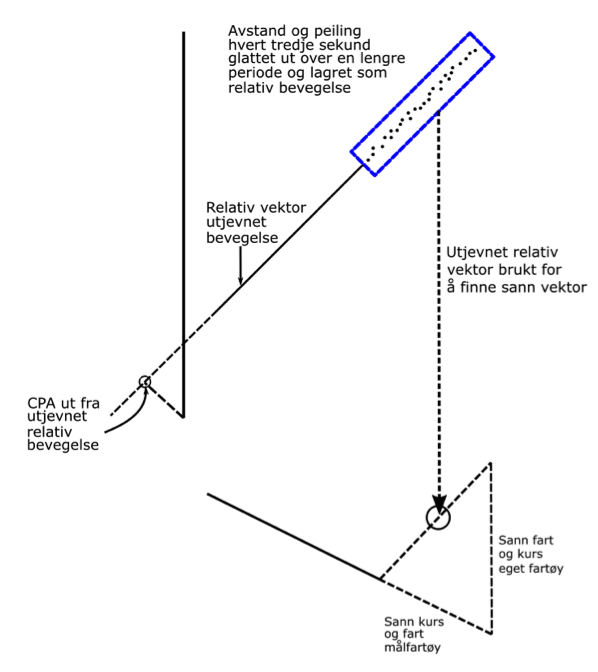
Figur 14 viser utfordringer med gjengivelse av relative vektorer til et målfartøy. En radar får flere relative avstander og peilinger til et målfartøy, og disse blir forsøkt utjevnet, slik at radaren kan presentere en stabil relativ vektor som ikke varierer for mye. På grunn av radaren har brukt relativt få peilinger og avstander for å presentere den første relative vektoren til målfartøyet, kan man oppleve at denne vektoren er noe upresis.
En radar kan vil ikke oppdatere målet med ny peiling og avstand før antennen har gjort en full rotasjon. De fleste radarer på fartøy har en rotasjonshastighet på rundt 22 omdreininger per minutt RPM). For hurtigbåter kan rotasjonshastigheten være opp til 44 omdreininger per minutt. Tiden mellom hvert plott kan man da finne med følgende formel:
$Tid = \frac{60\ sek./min.}{22\ rotasjoner/minutt} =\underline{2,7\ sek/rotasjon} $
$Tid = \frac{60\ sek./min.}{44\ rotasjoner/minutt} = \underline{\text{1,4 sek/rotasjon}} $
Vektordataene vil bli mer presise jo lengre tid som går etter at fartøyet ble plottet. Når ett av fartøyene svinger vil disse plottene endre retning, mens radaren fortsatt vil forsøke å utjevne plottene og presentere en rett linje. Den relative vektoren vil derfor være ustabil under og i en periode etter en manøver, og endringen i relativ vektor vil ha en relativ stor forsinkelse. Det er derfor viktig at en kursendring for å unngå kollisjon er tydelig. Da kan den også lettere observeres på radaren, men også lettere observeres visuelt. Dette vil man også se om man utfører en manuell radarplotting, så vil én grad feil i plottet for et fartøy som er langt unna medføre en relativ stor forskjell i CPA.
Om vår egen fart er feil
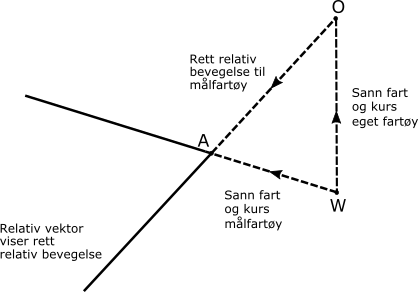
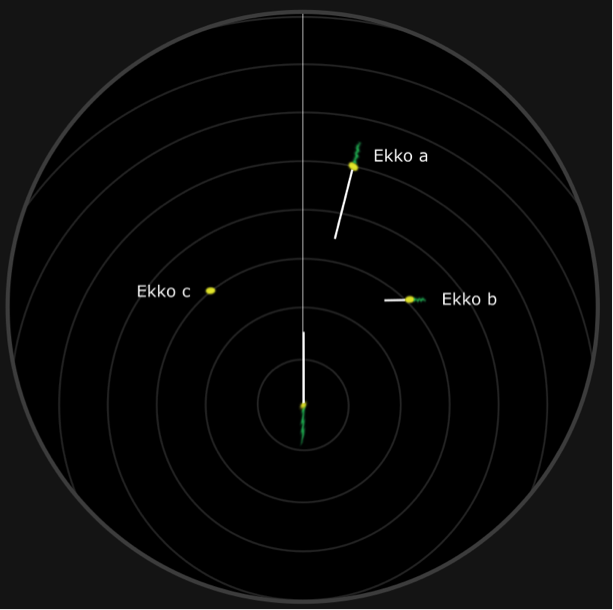
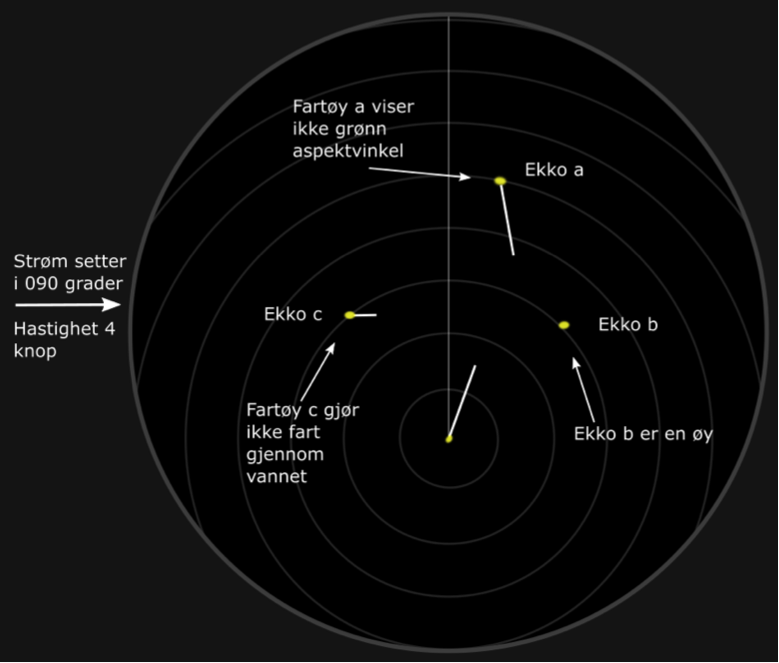
Det er viktig å merke seg hva som skjer på radaren om vår egen fart er feil. Kravet til godkjente ARPA-radarer er at de skal ha data for logget fart gjennom vannet (engelsk: Speed Thru Water, STW) og data fra en gyro. Selv om man mister farts- og kompassdata, så vil man få rett relativ vektor og informasjon om CPA og TCPA. Siden egen sanne vektor er feil, vil også målfartøyets sanne vektor bli feil.
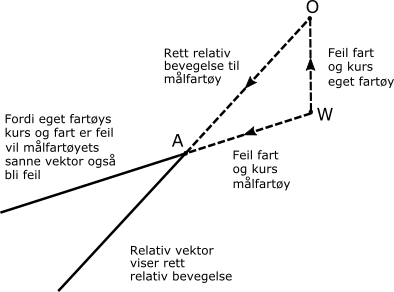
Dersom man mister data fra loggen og gyroen, så kan man bruke data fra GPS. Da får man fart over grunnen (Speed Over Ground, SOG) og beholden kurs over grunnen (Course Over Ground, COG). Man kan også stille inn farten manuelt på radaren. Ved å bruke logg og gyro, vil man få en sjøstabilisert radar, mens man ved bruk av beholden kurs og fart over grunnen vil få en grunnstabilisert radar. Utfordringen er at vektorene kan feiltolkes og i noen situasjoner kan man vurdere at feil fartøy har vikeplikt etter sjøveisreglene. Dette kan man tydelig se dersom man sammenligner figur 17 og figur 18. I figur 17 er radaren sjøstabilisert. Da vil presentasjonen av vektorene stemme med aspektvinklene man observerer visuelt. I figur 18 er radaren grunnstabilisert. Da vil de se ut som eget fartøy skal beholde kurs og fart og fartøy a skal vike. En visuell observasjon av fartøyet ville vist rød aspektvinkel, og eget fartøy skal vike da etter regel 15.