3. Usymmetrisk plassering og tungløft
Læremål:
- Studenten skal ha kjennskap til virkningen av last, herunder tunge løft, på skipets sjødyktighet og stabilitet.
- Kunne beregne krengevinkel på grunn av skjev lastefordeling eller tungløft
- Kunne beregne vekt som lastes/losses for å motvirke krengningen
- Kunne beregne krengevinkel når den overstiger 10 grader.
Usymmetrisk vektplassering
Hver enkelt vekt man plasserer om bord vil ha en VCG, LCG og TCG som angir vektens plassering. Når last, bunkers, ballast og andre vekter er plassert usymmetrisk om senterlinjen, vil det oppstå et krengemoment.

Figur 3.01.
På samme måte som G flytter seg opp og ned når vi flytter vekter vertikalt, vil tyngdepunktet også flytte seg ut til en side hvis summen av alle vektene ikke er plassert likt på hver side. Skipet vil få en krengevinkel til den siden tyngdepunktet har flyttet seg. Tyngdepunktet i denne retningen kalles TCG, Transverse Center of Gravity.

Figur 3.02.
På figur 3.2 vises de tre retningene skipets tyngdepunktet har. Skipets tyngdepunkt G har en plassering som angis fra aktre perpendikulær (LCG) fra kjøl i tverrskips retning (KG), og avstanden den har fra senterlinjen (TCG). Tyngdepunktet er tegnet langs skutesiden på denne figuren, men vil egentlig være plassert «inne i» skipet, som er markert der den stiplede blå linjen og den blå linjen møtes. I dette tilfellet er tyngdepunktet på styrbord side, og skipet vil ha et krengemoment til styrbord som gjør at skipet lister/krenger noen grader. Hadde tyngdepunktet vært i senterlinjen, ville det ikke oppstått noe krengemoment, og heller ikke noen krengevinkel. Senterlinjen blir også kalt diametrialplanet og kan også forkortes som CL.
Beregning av krengevinkelen
Vi kan beregne hvordan tyngdepunktet flytter seg som ved den tidligere GG-formelen man bruker ved tverrskips beregninger, men nå er armen avstanden fra senterlinjen, altså TCG.
$TCG = \frac{\text{Σvekt x arm}}{\mathrm{\Delta}}$ =$ \frac{\text{Σ krengemoment}}{\mathrm{\Delta}}$
For mindre krengevinkler (opptil ca 10 grader), så vil metasentret ligge i ro, men ved større krengevinkler så vil metasentret flytte seg. Det er derfor to ulike metoder på å beregne krengevinkel (Ø) på, ut fra hvor stor krengevinkelen er.
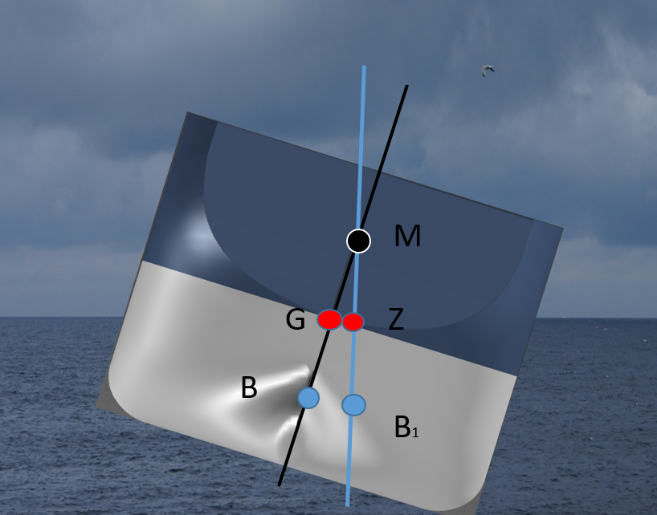
Figur 3.03
Ved mindre krengevinkler (opptil 10 grader), så kan vi finne vinkelen ved:
$\tan Ø = \frac{\text{TCG}}{\text{GM}}$ som gir Ø= tan-1 $\frac{\text{TCG}}{\text{GM}}$
Blir krengevinkelen her over 10 grader, så må man finne rett vinkel ved hjelp av GZ kurve og krengearm som blir beskrevet senere i dette kapittelet.
Eksempel 1 Beregning av krengevinkel med en vekt
Et skip med Δ= 8000 tonn, KM=8,0 meter og KG= 7 meter.
En vekt på 50 tonn blir flyttet fra senterlinjen og 10 m ut på styrbord side. Beregn skipets krengevinkel.
Svar:
$TCG = \frac{50 t x 10 m }{8000 t}$ = 0,063 m (på styrbord side)
Når TCG er funnet kan vi beregne krengevinkelen, og trenger da GM for å sette inn i formelen:
$\tan Ø = \frac{\text{TCG}}{\text{GM}}$
GM= KM – KG = 8 m – 7 m= 1,0 m
$\tan Ø = \frac{0,063}{1,0}$ = 0,063 → tan-1 0,063 = 3,6º til styrbord.
Av erfaring fra tidligere oppgaver i temaet tverrskipsstabilitet, har vi sett at når vi har flere vekter med ulike armer, så kan vi lage et momentskjema for å gjøre beregningene enklere og mer oversiktlige.
Dette kan vi også gjøre her, og ofte vil man beregne tverrskips stabilitet sammen med krengemomentet.
Eksempel 2 Beregning av krengevinkel med momentskjema.
Her har vi samme deplasement som forrige eksempel, bare at nå laster vi to vekter;
-
En vekt på 50 tonn som blir plassert 10 meter fra senterlinjen på styrbord side
-
En vekt på 20 tonn som blir plassert 6 meter fra senterlinjen på styrbord side
| Sted | Vekt | Arm (TCG) | Moment |
|---|---|---|---|
| Δ | 8000 | 0 | 0 |
| Vekt | 50 | 10 | 500 |
| Vekt | 20 | 6 | 120 |
| SUM | 8070 | 620 (stb) |
Beregner TCG= $\frac{\text{krengemoment}}{\mathrm{\Delta}}$ =$\frac{620 tm}{8070 tonn}$ = 0,0768 m
Regner krengevinkelen, GM er fortsatt 1,0 m:
$\tan Ø = \frac{0,0768}{1,0}$ = 0,0768 → tan-1 0,0768 = 4,39 º til styrbord.
Som regel vil oppgaver med usymmetrisk plassering av vekter og med tungløft også inkludere tverrskipsstabilitet. For når vi laster en vekt, så vil denne nye vekten påvirke tverrskipsstabilitet, krengning og trimmen. For å kunne beregne krengevinkelen trenger vi GM etter de nye vektene er tatt om bord, og det gjøres ved å beregne KG for deretter å beregne GM.
Dette gjelder også når vi losser vekter. Losser vi en vekt på styrbord side, vil det gi et krengemoment til babord.
I eksemplet nedenfor blir momentskjemaene kombinert med både tverrskips og krengning. Det beregnes ny KG og GM, samtidig som vi beregner krengemoment og krengevinkel.
Eksempel 3 Beregning av krengevinkel med flere vekter.
M/S Mercandian Importer har et dypgående på 5,10 meter og KG er beregnet til 4,42 meter. Skipet tar ombord følgende last:
- 100 tonn med VCG= 4,31 m og TCG= 5,2 m (babord side)
- 120 tonn med VCG= 4,25 m og TCG= 5,2 m (styrbord side)
- 90 tonn med VCG= 4,03 m og TCG= 4,5 m (babord side)
Svar:
Her må vi først bruke dypgangen til å finne rett vektdeplasement (Δ) før vi tar om bord de nye vektene.
Δ før restlast: 3584 tonn
KG før restlast: 4,42 m
| Sted | Vekt (tonn) | VCG (m) | V. Moment (tm) | TCG (m) Styrbord = pluss Babord = minus |
KRM (tm) |
|---|---|---|---|---|---|
| Δ | 3584 | 4,42 | 15841 | 0 | 0 |
| Last 1 | 100 | 4,31 | 431 | - 5,2 | - 520 |
| Last 2 | 120 | 4,25 | 510 | 5,2 | + 624 |
| Last 3 | 90 | 4,03 | 363 | - 4,5 | - 405 |
| Δ | 3894 | $\Sigma$ V.mom | 17145 | $\Sigma$ KRM | - 301 |
I eksempelet over så har vi funnet krengemomentet (KRM) ved å ta vekten av lasten og multiplisert den med TCG på alle de tre lastene. Deretter er disse summert, slik at vi får et totalt krengemoment, KRM. Her ble det -301 tm, og siden vi valgte babord side som minus, er dette et moment som gir oss en krengning til babord.
For å kunne beregne krengevinkelen, så trenger vi både GM og TCG.
Først beregnes KG. KG$= \frac{\text{Vertikalt moment}}{\Delta}$ = $\frac{17145 tm}{3894 t}$ = 4,403 m
Deretter må vi finne skipets KM i hydrostatiske data med skipets gjeldende Δ.
GM= KM – KG = 5,474 m – 4,403 m = 1,071 m
Deretter finner vi skipets TCG=
$TCG = \frac{\text{vekt x arm}}{\mathrm{\Delta}}$ = $\frac{\text{Σ Krengemoment}}{\Delta}$ = $\frac{301 tm}{3894 t}$ = 0,077 m babord.
Deretter beregnes krengevinkelen:
Ø= tan-1 $\frac{\text{TCG}}{\text{GM}}$ = tan-1 $\frac{0,077}{1,071}$ = 4,1⁰ til babord
Tungløft
Når vi beregner tungløft, så vil man beregne det på samme måte som ved usymmetrisk plassering. Beregning av tungløft ligger i faget skipsteknikk så det vil bare bli gitt et kort eksempel på det i denne boken.
Vekten virker igjennom bomnokkens høyde (VCG) og lengde (TCG).
Eksempel 4 Tungløft med krengevinkel under 10 grader.
«MS Mercandien Importer» skal ta et tungløft på 55 tonn. Før løftet tas om bord er skipets ∆ 3504 tonn og KG 4,3 m. Bomnokken er 21 m over kjølen, og løftet tas på styrbord side, 8 m fra diametrialplanet (CL ).
Hvor mange grader vil skipet krenge når løftet er klar av kaien?
Svar
| Tekst | Vekt | VCG | V mom | Avstand CL | KRM |
|---|---|---|---|---|---|
| ∆ | 3504 | 4,3 | 15067 | ||
| Tungløft | 55 | 21 | 1155 | 8 | 440 |
| ∆ | 3559 | ∑ V.mom | 16222 | ∑ KRM | 440 |
Ny KG = $\frac{\sum V.mom}{Nytt \mathrm{\Delta}R}$ = $\frac{16905 tm }{3559 t}$ = 4,558 m
Ny GM = KM – KG = 5,384 – 4,558 = 0,826 m
TCG = $\frac{ \sum KRM }{Nytt \mathrm{\Delta}R}$ = $\frac{440 tm}{ 3559 t }$ = 0,124 m
Tan ØStb = $\frac{TCG}{\text{Ny GM }}$ = Ø = tan-1 $\frac{G_1 \ G_2}{Gm} $ = $\frac{0,124 m }{0,826 m }$ = 8,538°
ØStb = 8,538˚
Kontravekt
For å begrense krengevinkelen kan man fylle ballast i en tank på motsatt side, eller plassere last på motsatt side.
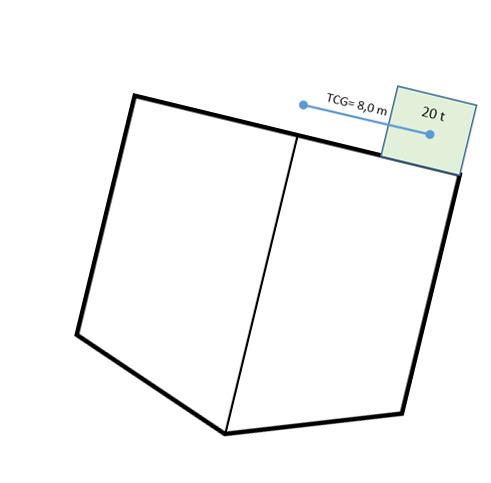
Figur 3.04. Dekkslasten har en vekt på 20 t og er plassert på styrbord side, 8 m fra senterlinjen. Samlet gir dette er krengemoment på 160 tm ts
For å få 0 i krengemoment, så må krengemomentet på begge sider være like store. Som denne figuren viser, så må vi ha et krengemoment på 160 tm på babord side for å ligge uten krengning.
Hadde man satt tilsvarende dekkslast med samme vekt og avstand til senterlinjen på babord side, så ville skipet rettet seg opp igjen.
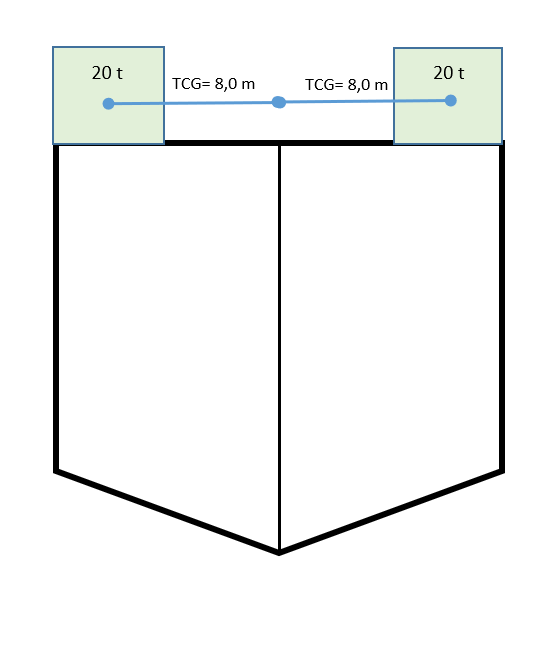
Figur 3.05.
Det er nå dekkslast med samme vekt og avstand fra senterlinjen på begge sider, og skipet ligger nå uten krengning.
Hadde lasten på babord side blitt plassert med halve avstanden fra senter, her 4 meter, så måtte vekten være dobbelt så tung for å få 0 i krengemoment.
20 t x 4 m= 80 tm
Dobler vekten:
40 t x 4 m= 160 tm
Man kan også velge seg ut en ballasttank på motsatt side for å oppveie krengningen.
Eksempel 5 Beregning av kontravekt.
Man finner all informasjon om lasterom og tanker i ressursheftet til båten, og henter ut TCG (og eventuelt LCG og VCG) for ønsket tank. Her vises en del av oversikten over ballasttankene på MS Sidus. Hvis MS Sidus hadde hatt et krengemoment til styrbord på 1000 tm, så kan vi velge å fylle en ballasttank på babord side. I dette eksempelet velger vi bunntank 1 babord, og tar ut TCG på den tanken som er 5,30 m. I denne tabellen ser vi at TCG står med fortegn, men vi må alltid sjekke om fortegnet stemmer overens med hvilken siden vi selv har valgt pluss eller minus.
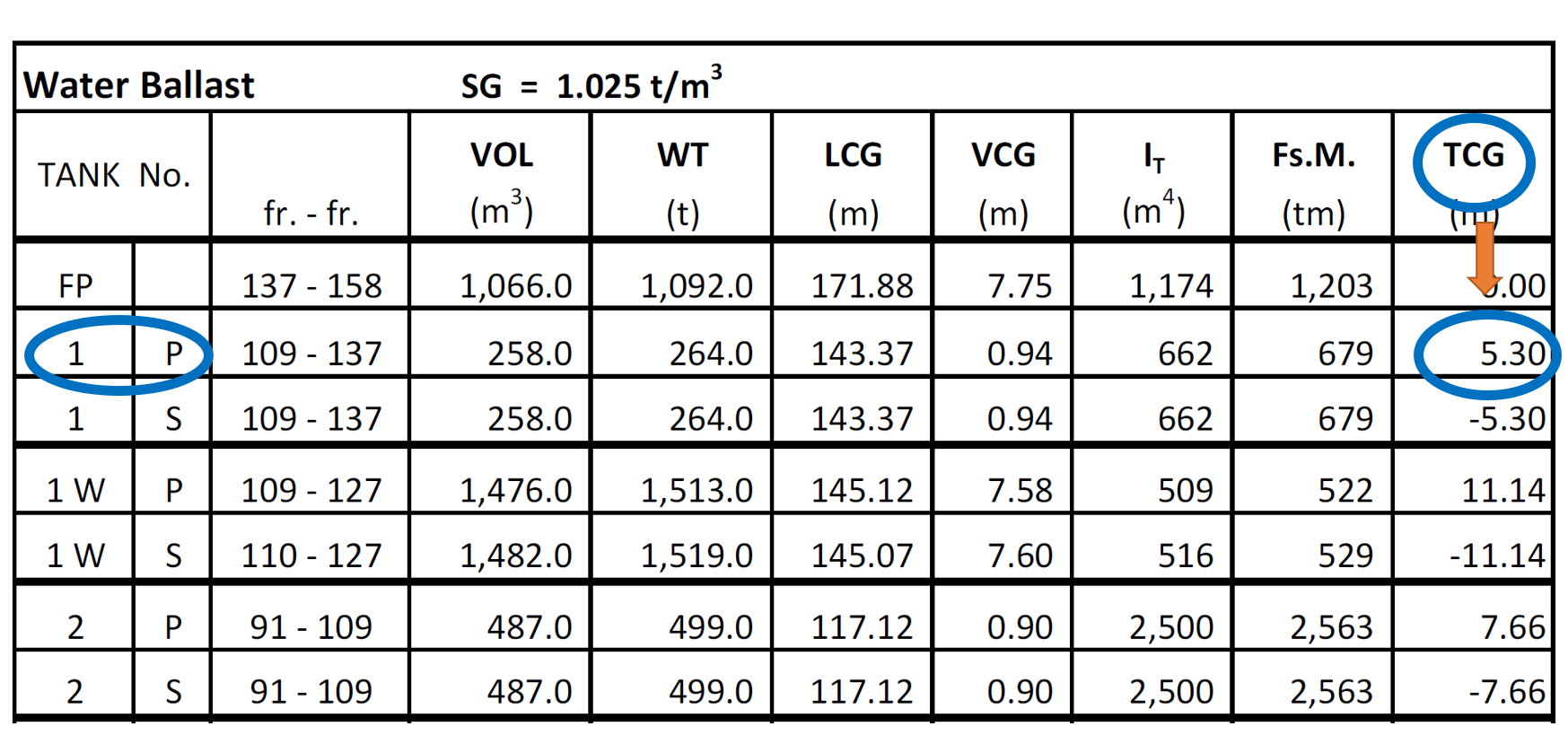
Figur 3.06.
For å beregne hvor mange tonn ballast som skal fylles, så bruker vi samme prinsipp som ved tverrskips.
Vekt x arm = Moment
Her er armen TCG, og da er momentet krengemoment.
Vekt x TCG = Krengemoment
I dette tilfellet så vet vi krengemomentet og vi har funnet TCG for ballasttanken, så vi kan beregne vekten som må til.
$vekt = \frac{\text{krengemoment}}{\text{TCG}}$ $= \frac{1000 tm}{5,30 m}$ = 188,7 t
Det vil si at vi må fylle 188,7 t ballast i tank 1 P (babord) for å få samme krengemoment som på styrbord side.
Vekt x TCG = Krengemoment
188,7 t x 5,30 m= 1000 tm.
I plansjene til MS Mercandien Importer står TCG oppført med ± 4,40 m. Det betyr at babord tanken har tyngdepunkt 4,40 m fra senterlinjen på babord side, og styrbord tanken har tyngdepunkt 4,40 m på styrbord side. Man velger selv hvilken side man vil ha pluss og minus på, så lenge alle vektene på babord/styrbord side har samme fortegn.
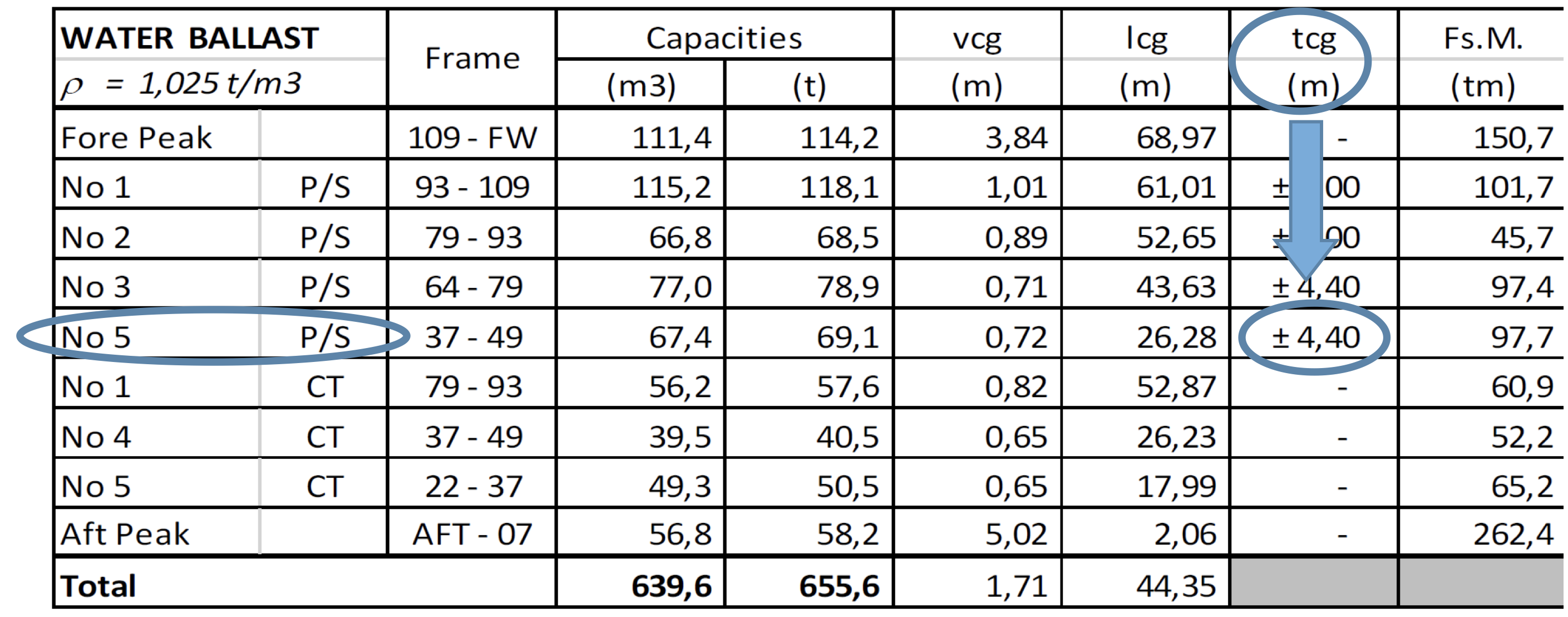
Figur 3.07.
Eksempel 6 Beregning av krengevinkel etter lasting av containere med kontravekt.
MS Mercandien Importer har en TRet på 5.20 meter og TCG 0.03 meter på babord. Skipet skal laste to containere på 12 tonn hver med en TCG 2.0 meter fra senterlinjen på styrbord side. Skipets KG før containerlasten er 4.8 meter, og lastens VCG er 7.8 meter.
- Beregn skipets krengevinkel etter containerne er lastet
- Hvor mye kontravekt må du bruke for å holde skipet med null i list/ingen krengning? Bruk ballast WT 3 S TCG 2,25 meter.
Løsning
Skipet ligger med en krengning mot babord siden skipets TCG er 0,03 m på babord side, det vil si at skipet har et krengemoment til babord, og man kan også beregne krengevinkelen skipet har før restlast. I dette tilfellet trenger vi kun krengemomentet, som vi finner ved:
Krengemoment (KRM) = Δ (vekt) x TCG (arm)
Vi har ikke fått oppgitt skipets Δ i dette eksempelet, så vi må finne det i ressursheftet ved hjelp av TR=5,20 m → Δ= 3665 t. her har jeg valgt minus på babord krengemoment, og pluss på styrbord moment.
| Sted | Vekt (tonn) | KG/VCG (m) | V.moment (tm) | TCG (m) | KRM (tm) |
|---|---|---|---|---|---|
| Δ | 3665 | 4,8 | 17592 | -0,03 | -109,95 |
| Containere | 24 | 7,8 | 187,2 | 2 | 48 |
| Δ | 3689 | $\sum$ | 17779,2 | $\sum$ | -61,95 |
Vi beregner først KG og GM:
Ny KG = $\frac{\sum V.mom}{Nytt \mathrm{\Delta}R}$ = $\frac{17779,2 tm }{3689 t}$ = 4,82 m
Ny GM = KM – KG = 5,416 – 4,82 = 0,596 m
TCG = $\frac{ \sum KRM }{Nytt \mathrm{\Delta}R}$ = $\frac{61,95tm}{ 3689 t }$ = 0,017 m
Tan ØStb = $\frac{TCG}{\text{Ny GM }}$ =$\frac{0,017 m }{0,596 m }$ = 0,028
ØStb = 1,614˚
Beregner hvor mye kontravekt som skal fylles i ballasttank WT3 S med TCG 2,25 meter:
$vekt = \frac{61,95 tm}{2,25 m}$ = 27,53 t
Det må fylles 27,53 tonn med ballast for å opphøre krengningen/ligge med 0 list.
Eksempel 7 MS Sidus krengning med containere.
M/S MS Sidus har lastet en bulklast og har følgende kondisjon etter bulklasting:
Deplasement= 48342 t KG= 11.70 m List = 2˚ til stb
En skal sluttlaste med TEU containere som har enhetsvekt= 14 tonn. Disse skal lastes i BAY 34. Man skal kun laste TEU på babord side TCG= 6.16 m. TEU fordeles likt mellom tier 82 og 84.
a) Hva er skipets krengemoment før TEU ble tatt om bord?
b) Hva blir ny KG/GM etter at TEU er tatt om bord?
c) Hva blir skipets krengevinkel etter at TEU er tatt om bord?
For å rette opp skipet bestemmer en seg for å ballasttank WB 4P. Denne tanken var tom fra før.
d) Hvor mye ballast må fylles for å rette opp skipet?
e) Hva blir ny G2M etter at ballast er tatt om bord?
Løsning.
Her må vi først beregne krengemomentet som gjør at skipet ligger med 2⁰ til styrbord. Vi snur om formelen for å finne krengevinkel:
KRM
KRM = GM x $\Delta$ x $\tan{2°}$.
Her trenger vi først å finne GM ved hjelp av KM (hydrostatiske data) og KG som er oppgitt i oppgaven.
GM= KM - KG= 13,27 m - 11,7 m= 1,57 m
a) Krengemoment= GMxΔxtan 2 = 1,57m x 48342t x tan 2= 2650,4 tm
b) Det er plass til 10 TEU på tier 82 og 10 TEU på tier 84 ( felles VCG= 24,29 m) i Bay 34
| Sted | Vekt | VCG | V.Moment | TCG | KRM |
|---|---|---|---|---|---|
| Δ | 48342 | 11,7 | 565601,4 | 2650,4 | |
| Tier 82 | 140 | 22,98 | 3217,2 | -6,16 | -862,4 |
| Tier 84 | 140 | 25,6 | 3584 | -6,16 | -862,4 |
| Δ | 48622 | 572402,6 | 925,6 |
KG = 11,77 m
KM = 13,28 m
GM = 1,51 mKrengevinkel = $\frac{KRM }{Δ \text{x} GM}$ = 0,013
Ø= tan-1 = 0,745
For å kunne beregne kontravekten, så trenger vi å finne ballasttankens TCG i skipets tabeller.
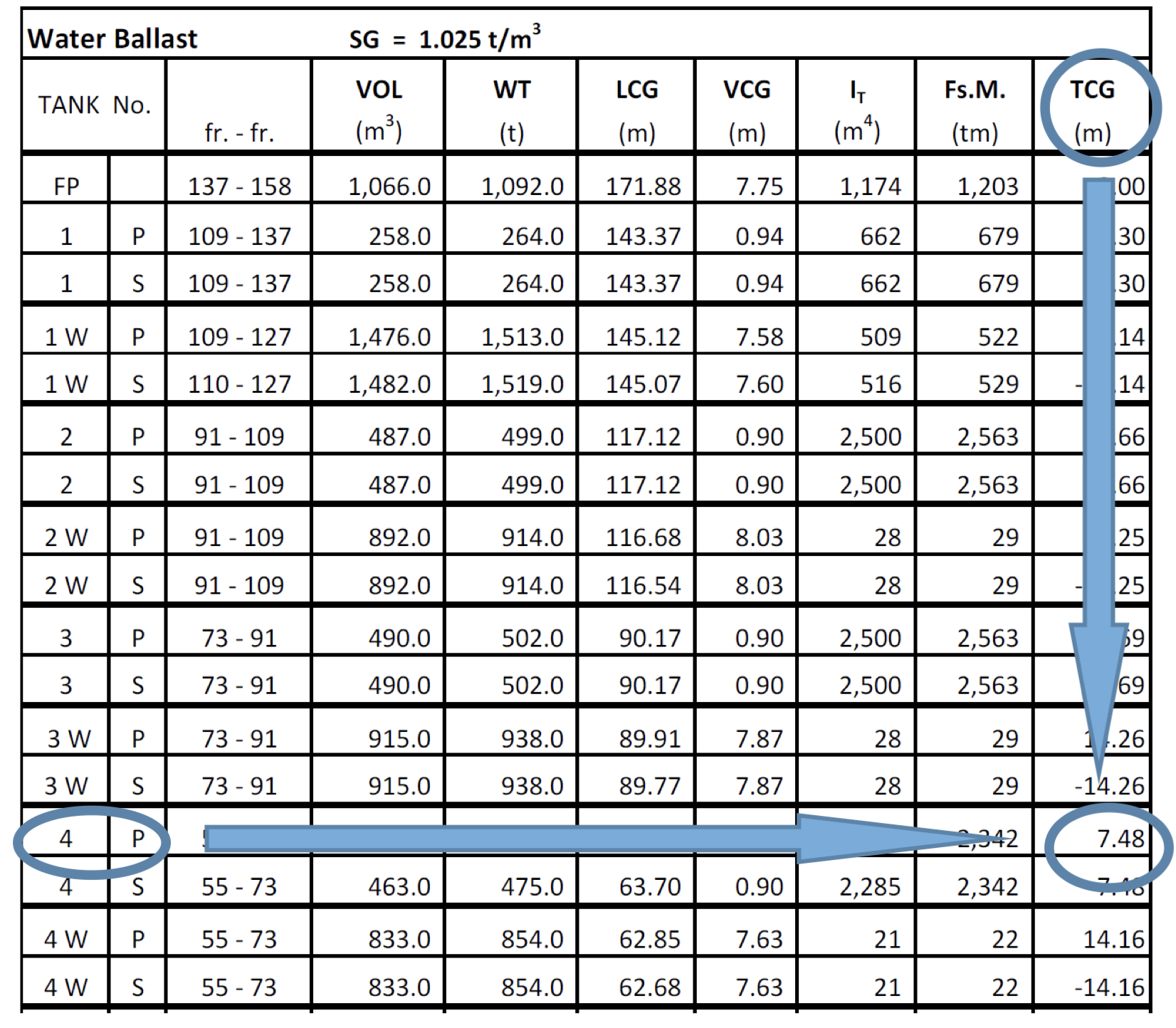
Figur 3.08.
Her ser vi at denne tankens TCG er 7,48 m på babord side. Siden vi allerede har regnet krengemomentet til styrbord med pluss, så må vi bruke minus på vektene på babord side.
vekt å fylle: $\frac{KRM}{ arm (TCG)}$ = 123,74 tonn
| Sted | Vekt | VCG | V.Moment | TCG | KRM | FSM |
|---|---|---|---|---|---|---|
| Δ | 48622 | 572402,6 | 925,6 | |||
| ballast | 123,74 | 0,18 | 22,3 | 7,48 | 925,6 2363 | |
| 48745,74 | 572424,9 | 1851,2 | 2363 |
KG2= 11,79
KM= 13,28
G2M= 1,49
Krengevinkel som overstiger 10°
Som beskrevet tidligere så er måten vi har beregnet krengevinkelen kun nøyaktig krengevinkler på opptil 10⁰ for da vil oppdriftskraften fortsatt virke gjennom Metasenteret. Når krengevinkelen blir større enn 10⁰ virker ikke denne kraften gjennom metasenteret lengre, og vi må ta hensyn til reststabiliteten. Dette gjøres ved å beregne GZ, og tegne opp en GZ kurve. Deretter må beregne og tegne krengearmen inn i GZ kuven og lese av rett krengevinkel fra kurven.
Eksempel med krengning over 10°
MS Mercandien Importer skal ta et tungløft på 65 tonn. Før løftet tas om bord er skipets totale DW 1500 tonn og GM 1,11m. Bomnokken er 20 m over kjølen, og løftet tas 7,5 m fra diametrialplanet (CL ) på barbord side.
- Hvor mange grader vill skipet å krenge når løftet er klar av kaien?
- Hvor mange tonn ballast må fyllest som kontravekt for å få en krengevinkel under 10°?
- Hva blir ny krengevinkel når man har fylt ballast?
Svar
Finner ∆ før lasting
∆= DW + LS = 1500t + 1060t = 2560t
Finner KG før lasting
KG = KM – GM = 5,36 m – 1,11m = 4,25m
Vi finner ny KG og horisontal forskyvning av G
| Tekst | Vekt VCG | V mom | TCG/Avstand | CL | Kr.mom |
|---|---|---|---|---|---|
| ∆ | 2560 | 4,25 | 10880 | ||
| Tungløft | 65 | 20,00 | 1300 | 7,50 | 488 |
| Nytt ∆ | 2625 | ∑ V.mom | 12180 | ∑ KRM | 488 |
Ny KG = $\frac{\sum V.mom}{Nytt \mathrm{\Delta}}$ = $\frac{12180tm}{2625t}$ = 4,64m
Ny GM = KM – KG = 5,34m – 4,64m = 0,70m
TCG = $\frac{ \sum KRM }{Nytt \mathrm{\Delta}}$ = $\frac{488tm}{ 2625t}$ = 0,18590 m
Tan Øbb = $\frac{TCG}{\text{Ny GM }}$ =$\frac{0,18590 }{0,70}$ = 0,26558 Øbb = 14.8˚
Krengevinklen er større en 10˚, må sette opp GZ kurve.
GZ = MS + GM x sin Ø
GZ 10˚ = 0,010 + 0,70 x sin 10˚ = 0.132m
GZ 20˚ = 0,080 + 0,70 x sin 20˚ = 0.319m
GZ 30˚ = 0,260 + 0,70 x sin 30˚ = 0.610m
GZ 45˚ = 0,205 + 0,70 x sin 45˚ = 0.670m
GZ 60˚ = -0,095 + 0,70 x sin 60˚ = 0.511m
GZ 75˚ = -0,555 + 0,70 x sin 75˚ = 0,121m
Vi plotter inn linjen G1G2 x CosØ
Ø = 0˚ TCG x cos Ø = 0,18590 x cos 0˚ = 0,186m
Ø = 20˚ TCG x cos Ø = 0,18590 x cos 20˚ = 0,175m
Ø = 45˚ TCG x cos Ø = 0,18590 x cos 45˚ = 0,132m
Ø = 60˚ TCG x cos Ø = 0,18590 x cos 60˚ = 0,093m
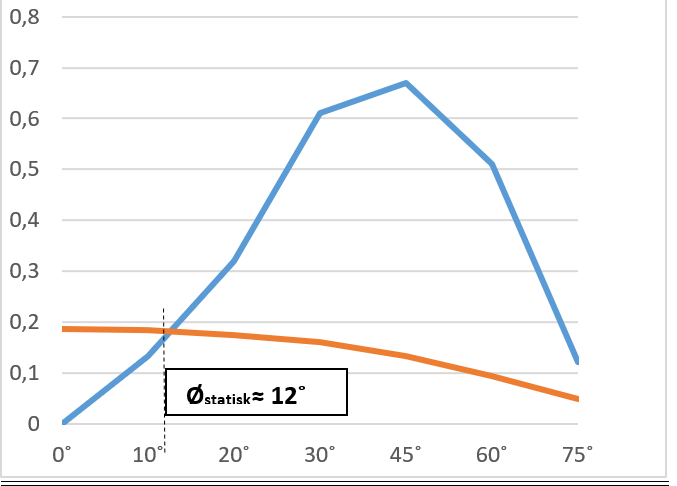
Gjør et overslag for å fine hvor mye ballast som må fyllast for at krengevinkeln skal bli mindre en 10˚.
Kr.mom = Tan10˚ x Gm x ∆ = Tan10˚ x 0,70m x 2625t = 324 tm
Krengemoment å endre = 488 tm – 324 tm = 164 tm
Bruker ballasttank 2 styrbord til kontravekt med TCG 4,0m.
Vekt å flytte = $\frac{\text{Kr.mom}}{\text{ Arm}}$ = $\frac{164tm}{ 4m}$ = 41,0 tonn
Setter opp mommentskjema for å finne ny krengevinke.
| Tekst | Vekt | VCG | V mom | FSM | Avstand CL | Kr.mom |
|---|---|---|---|---|---|---|
| ∆ m/tungløft | 2625 | 12180 | 488 | |||
| 2 stb | 41 | 0,89 | 36,5 | 45,7 | -4 | -164 |
| Nytt ∆ | 2666 | ∑ V.mom | 12216,5 | 45,7 | ∑ KRM | 324 |
Ny KG = $\frac{\sum V.mom}{Nytt \mathrm{\Delta}R}$ = $\frac{12216,5tm + 45,7 tm}{2666t}$ = 4,599m
Ny GM = KM – KG = 5,329 – 4,599 = 0,73m
TCG = $\frac{ \sum KRM }{Nytt \mathrm{\Delta}R}$ = $\frac{324tm}{ 2666t }$ = 0,122 m
Tan Øbb = $\frac{ TCG }{\text{Ny GM }}$ =$\frac{0,122m }{0,73m}$ = 0,166 gir Øbb = 9,4˚

