1. Skipets dimensjon og form
Læremål
Etter å ha gjennomgått dette kapittelet skal studenten ha kompetanse om:
- Skipets hoveddimensjoner
- Volumdeplasement og vektdeplasement
- Arkimedes lov
- Bruk av lasteskala, kunne ta ut de hydrostatiske verdier, samt ha en forståelse av disse.
- Ha kjennskap til Formkoeffisienter, kunne beregne disse.
- Ha kjennskap til konstruksjonselementer som inngår i et skrog.
- Ha kjennskap til Fribordsmerke og lastelinjekonvensjonen.
- Ha kjennskap til linjetegninger og målkonvensjonen.
- Ha kjennskap til motstand på skip og skrog.
- Ha kjennskap til hvordan man beregner areal ved hjelp av Simpson formel.
Dimensjoner til et skip.
Til måling av fysiske størrelser for et skip så benyttes SI systemet (Système international d'unités, Fransk; Det internasjonale enhetssystem) slik som meter (m) og kilogram (kg), hvor 100 kg er 1 tonn (metrisk tonn). Dette systemet er også kalt for det metriske systemet. I denne boken blir 1000 kg betegnet som: Tonn, Metrisk tonn og Tonnes (Engelsk) og det er fordi alle disse tre begrepene blir benyttet i dag til sjøs.
Lengde:
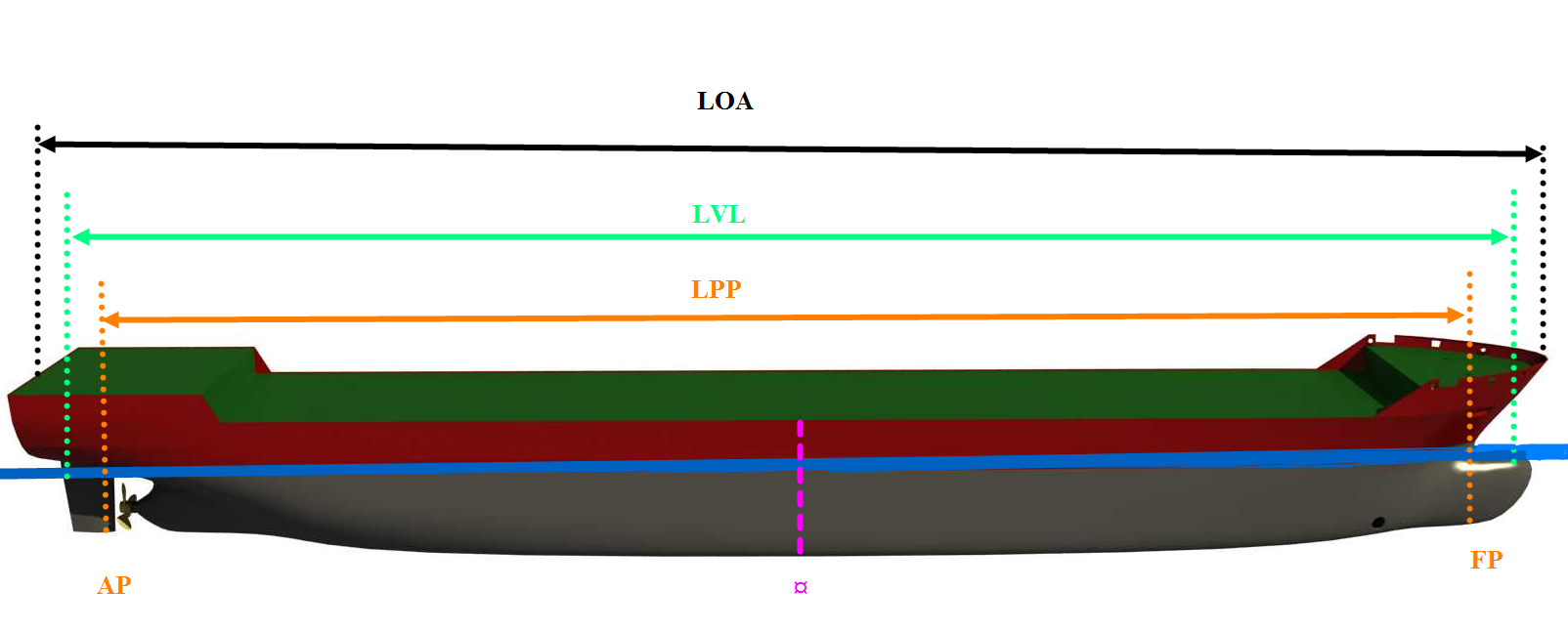
Figur: 0101 viser lengde dimensjoner
LOA: (Length overall, Engelsk) Lengde overalt: Den største utvendige lengden av skroget. Denne lengden oppgis før ankomst havn og blir tatt i betraktning når sluser skal benyttes og når skipet må snues helt rundt i et havnebasseng.
LVL: (Length of waterline, Engelsk) Lengde i vannlinjeplanet. Denne varierer med dypgående og har betydning for hvilken fart skipet oppnår.
LPP: (Length between perpendiculars) Lengde mellom perpendikulære. Opprinnelig ble betegnelsen fra akterkant av akterstevn til forkant av forstevn benyttet. I akterkant av akterstevn ble rorstammen montert. Etterhvert ble det ulike former på skroget og hvordan roret ble montert. I dag benyttes senter av rorstammen som utgangspunkt akterut. Når et skip er fullt lastet og har en horisontal vannlinje, det vil si skipet har ikke trim, der hvor vannlinjen skjærer forkant av forstevn vil være utganspunktet forut. LPP blir i formelsamlingene betegnet som L.
AP: Aktre perpendikulær, den vertikale linjen gjennom rorstammen senterline.
FP: Forre perpendikulær, den vertikale linjen som går gjennom skjæringspunktet mellom skroget og den vannlinjen skipet har når det er fullt lastet.
¤: Nullkryss spantet (midtspantet), den vertikale linjen gjennom det punktet som ligger midt i mellom FP og AP.
Bredde og dybde:
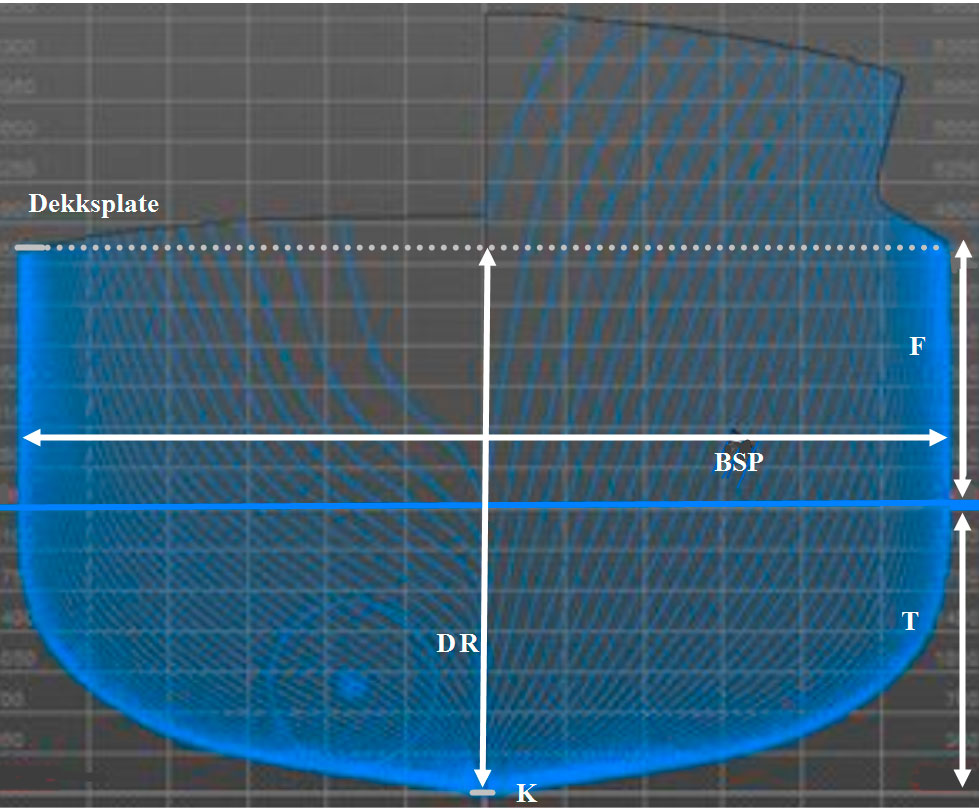
Figur 0102 viser bredde og dybde dimensjoner
DR: Dybde i riss, måles på skipet halve lengde, det vil si ved nullkryss spantet (midtspantet). Måles fra overkant av kjølplaten opptil underkant av dekksplaten i borde. Riss (Moulded, Engelsk) vil si å måle på innsiden.
BSP: Bredde på spant, måles på utvendig på spantene på skipets bredeste del som vil være ved nullkryss-spantet (midtspantet). Utvendig på spantene vil si innvendig på hudplatene. (Breadth moulded, Engelsk). Største bredde blir på utsiden av hudplatene.
T: Dypgående, angir avstand fra vannlinjen til underkant av kjølplaten ved nullkrysspantet (midtspantet). Dypgående leses av på fotmerket som er lokalisert ved nullkrysspantet (midtspantet).
F: Fribord, angir avstand fra overkant av dekksplaten i borde ved nullkrysspantet (midtspant) ned til vannlinjen.
K: Kjølplate, normalt den tykkeste platen på skroget, stikker litt dypere enn bunnplatene. Overkant av kjølplaten betegnes som basislinjen (grunnlinjen) og det er i fra denne som brukes som referansepunkt på vertikale avstander til forskjellige hydrostatiske verdier.
Deplasement: Oppgis i vektdeplasement og volumdeplasement. Deplasement kommer fra det Engelske ordet displacement, som betyr å fortrenge. Se på figur under og tenk at utgangspunktet er at det store bassenget er fylt helt opp til avløpsrenna med vann, ingen båt er plassert i bassenget og det lille avløpsbassenget er tomt. En båt blir heist med en kran og plasser oppe i det store bassenget og det vil medføre at all overflødig vann vil renne over til det lille bassenget. Det lille bassenget er rektangulært i form og volum av den fortrengte væskemengde vil bli = Lengde x Bredde x Høyde. Lengde, bredde og høyde er i meter og svaret vil bli i kubikkmeter (m3). Volum av det fortrengte væskemengden vil også bli volumdeplasement til båten da disse to er like stor. Volumdeplasement er volum av skroget under vannlinjen. Vektdeplasementet vil da være lik vekten av den fortrengte væskemengde, som blir: volum x tetthet. Tetthet er hva væsken veier i vekt dividert på væsken sitt volum, oppgis i kilogram/liter eller i Tonn/m3.
$\frac{\mathbf{\mathrm{\Delta}}}{\mathbf{\nabla}}\mathbf{= p\ }$, $\mathbf{\mathrm{\Delta}}$ = vektdeplasement ( Tonnes),
$\mathbf{\nabla}$ = Volumdeplasement (m3), p = tetthet = tonn/m3
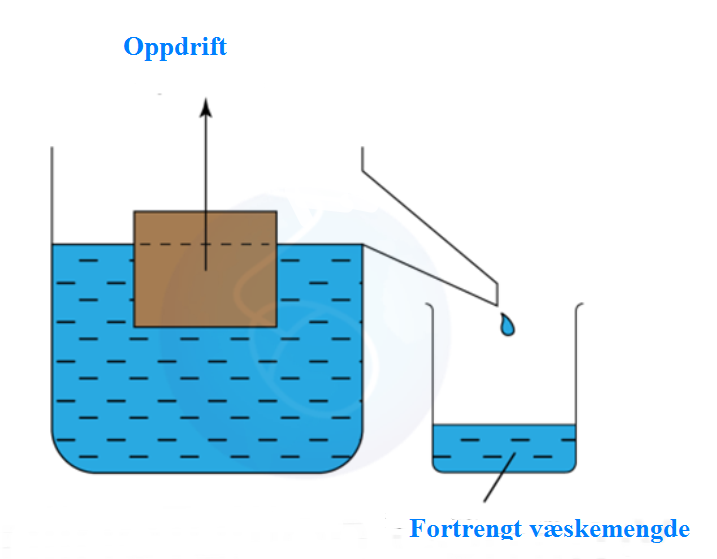
Figur 0103 Arkimedes lov
Så hvordan beregner man vektdeplasement til et skip i normale daglige operasjoner? Et skip har dypgangsmerker eller fotmerker som det også kalles, disse er plassert på skroget forut, midtskip og akterut på begge sider. Selve dypgangsmerkene er plassert på skroget etter en bestemt tetthet og det er som oftest saltvann tetthet som er 1,025 tonn/m3. På dypgangsmerkene leser man av hvor vannlinjen krysser disse. Er tettheten lik 1,025 tonn/m3 og hvis skipet har ingen trim eller list , det vil si at vannlinjen er helt horisonta, så kan man gå inn i en lasteskala og lese direkte ut hvor stort vektdeplasementet er.

Figur 0104 viser en modell av skipet M/S Ross Mount, som blir kalt for M/S Linda i Norske maritime lærebøker. Her kan man se dypgangsmerkene på babord side.
Tar et eksempel med M/S Linda: Det leses av på dypgangsmerket midtskips, det er ingen trim eller list, vannlinjen er horisontal og skipet ligger i saltvann. Dypgangsmerkene er merket opp for hver 20 cm og hvert dypgangsmerke er 10 cm høy, det vil si det er 10 cm mellom hvert merke. Vannlinjen er helt øvrekant av 8,80 m og da blir dypgående 8,90m. Se figur 0105.
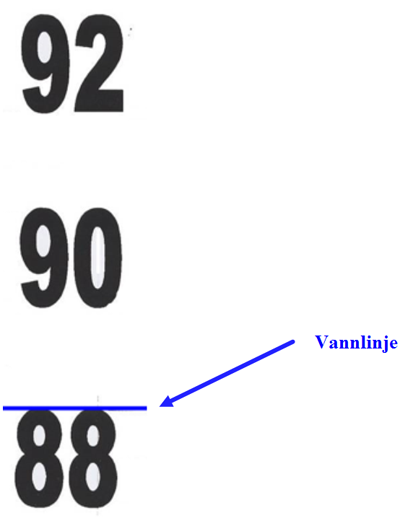

Figur 0105 skisse av dypgående midtskip for Linda og et utsnitt bilde av dypgående midtskip
Skisse 0106 viser et utsnitt av lasteskalaen for Linda. Helt øverst står det at den er laget for saltvann (1,025 tonn/m3). Den røde stiplete korte linjen indikerer dypgående 8,90 m og i den første kolonne angis vektdeplasementet til dette dypgående. Vektdeplasementet er 21223 Tonnes, før i tiden var det kraftig forstørret lasteskala hengt opp på skottet inne på overstyrmannens kontor, dette for å lese av nøyaktig vektdeplasement og andre hydrostatiske verdier. Neste kolonne viser Deadweight som blir dødvekt på Norsk.
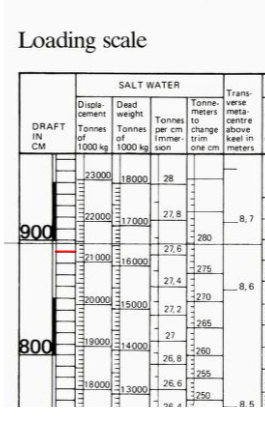
Figur 0106 viser et utsnitt av lasteskalaen for Linda.
Lettskip:
Lettskipdeplasement er vekten av skip uten last, bunkers, ferskvann og reservedeler. Lettskips deplasement er vekten av et tomt skip, det vil si vekt av skroget og overbygningen, maskineri og utrustning.
Dødvekt:
er skipets bæreevne, det vil si hva det er i stand til å ta med seg av last, bunkers, ferskvann, smørolje, proviant og reservedeler.
Ved dypgående på 8,90 meter leses Dødvekt av til 16328 Tonnes. Hvis man kjenner til både vektdeplasement og dødvekt så kan lettskip (deplasement) beregnes ved å: Deplasement -- dødvekt. Lettskip deplasement for M/S Linda er: 21223 Tonnes -- 16328 Tonnes = 4895 Tonnes.
Formkoeffisienter:
Formkoeffisienter brukes til å beskrive skrogets form på en enkel måte og hjelper til å sammenligne skrogformer. Disse er veldig nyttige i starten av et byggeprosjekt fordi de karakteriserer egenskaper til et fartøy slik som for eksempel lasteutnyttelse og motstand i vannet. Det vil være bortkastet tid og penger hvis man skulle bygge en modell først slik som figur 0104 viser. Formkoeffisienter er dimensjonsløse (-) eller ubenevnt fordi ved beregning av formkoeffisienter så blir det samme benevning over brøkstrek som under. En formkoeffisient forteller om forholdet vedrørende to sammenligninger og hvor beregningen av formkoeffisienten blir 1 eller mindre enn 1.
Blokk-koeffisient: (CB)
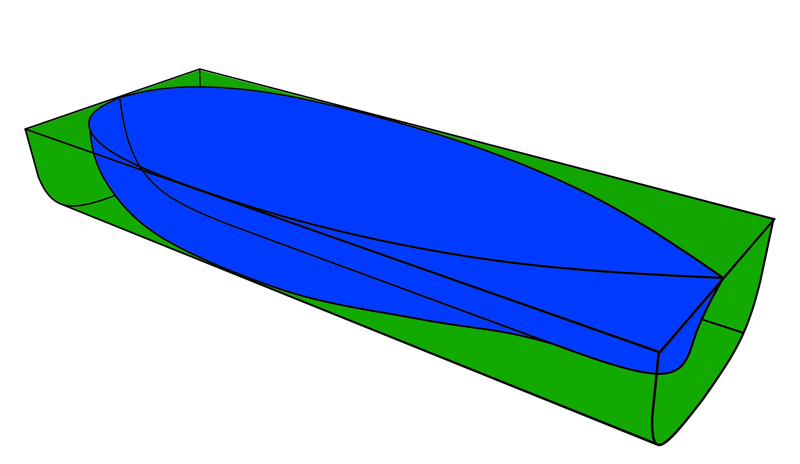
Figur 0107 viser Blokk-koeffisient
Det blå er volumdeplasement og det grønne er en rektangulær kasse som er like lang og bred og høy som volumdeplasementet (volum av skroget under vannlinjen). Blokk koeffisient er coefficient block på engelsk og har forkortelsen CB. Den beskriver forholdet mellom volumdeplasementet og den rektangulære kassen.
Formel for CB
CB = $\frac{\nabla}{L\ \times B\ \times T}$ $\nabla\ = \ $volumdeplasement (m3), LPP (m),B (bredde) (m), T (dypgående) (m).
En pram har en form som en rektangulær kasse og CB for er en pram blir 1.
Fregatt «Fridtjof Nansen» har følgende deplasement og mål:
$\mathrm{\Delta}$ = 5290 Tonnes, LPP = 134 m , bredde = 16,8 m og T = 7,60 m.
Hva blir CB ?
CB = $\frac{\nabla}{L\ \times B\ \times T}$ $\nabla$ = $\ \frac{\mathrm{\Delta}}{p}$= $\frac{\ \ 5290\ Tonnes\ }{\ 1,025\ tonn/m^3\ }$ = 5160, 97 m3.
CB = $\frac{\nabla}{L\ \times B\ \times T}$ = $\frac{5160,\ 97\ \ m^3}{134\ m\ \times 16,8\ \ m\ \ \times 7,60\ \ m\ }$ = 0, 30 (-).
En blokk-koeffisient på 0, 30 er veldig lavt som viser til et like smekker skrog som vikingskipene.

Figur 0108 viser et bilde av "Kvitbjørn, som tilhører Rederiet Norlines
Følgende opplysninger om «Kvitbjørn»:
LPP 117,55 m, Bredde 20,80 m, T= 6,00 m, DW = 5000 Tonnes (Dødvekt). LS ∆ = 5070 Tonnes (Lett skip).
Hva blir CB?
CB = $\frac{\nabla}{L\ \times B\ \times T}$ =, ∆ = LS + DW = 5070 Tonnes + 5000 Tonnes = 10070 Tonnes.
$\nabla$ =$\ \frac{\mathrm{\Delta}}{p}$ = $\ \frac{10070\ \text{Tonnes}}{1,025 \text{tonn}/m^3} $= 9824 m3
CB = $\frac{9824\ m^3\ }{117,55\ \ \times 20,80\ m\ \ \times 6,00\ m}$ = 0,67 (-)
Blokk koeffisient på 0,67 er også bra med hensyn på fart i gjennom vannet. Blokk koeffisient til et stort tankskip vil være rundt 0,85 (-) da disse er skapt for å ta mye last med seg og der fart igjennom vannet er mindre vesentlig, til et Container skip vil være rundt 0,7 (-).
Vannlinjearealet koeffisient (CW):
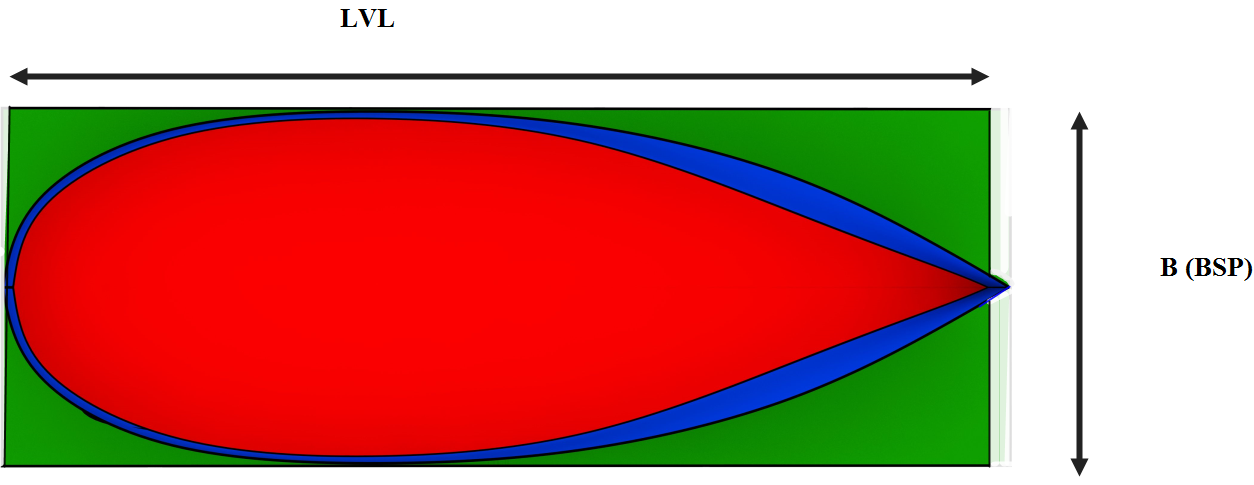
Figur 0109 Viser Vannlinjearealet finhetskoeffisient.
Det røde er vannlinje arealet (Engelsk Area water, AW) og det grønne viser rektangelet av LVL og BSP. LVL kan også være lik LPP. Et skip har AW = 2475 m2, skipet har L (lengde): 150 m og B (bredde): 22 m for dette vannlinjearealet..
Hva er CW?
CW = $\frac{\text{AW}}{L \times B}$ = $\frac{2475 m^2}{150 m \times 22 m}$ = 0,75 (-)
Et skip har L (lengde): 55 m og B (bredde): 12 m for et bestemt vannlinjeplan.
CW er oppgitt til å være 0,67.
Hvor stort er AW for dette vannlinjeplanet?
CW = $\frac{\text{AW}}{L \times B}$→ AW = CW × L × B = 0,67 × 55 m × 12 m = 442,12 m2.
CW vil variere med dypgående for et og samme skip. Hvis man tar utgangspunkt i fullastet skip så vil et fyldig skip ha en CW på omtrentlig 0,85 (-), med middelsfyldighet vil CW bli 0,75 til 0,80 (-) og for et skip med skarpe kanter er CW lik 0,7 (-). Vannlinje arealet størrelse og form har stor betydning for skipets stabilitet.
Midtspantkoeffisienten (CM):
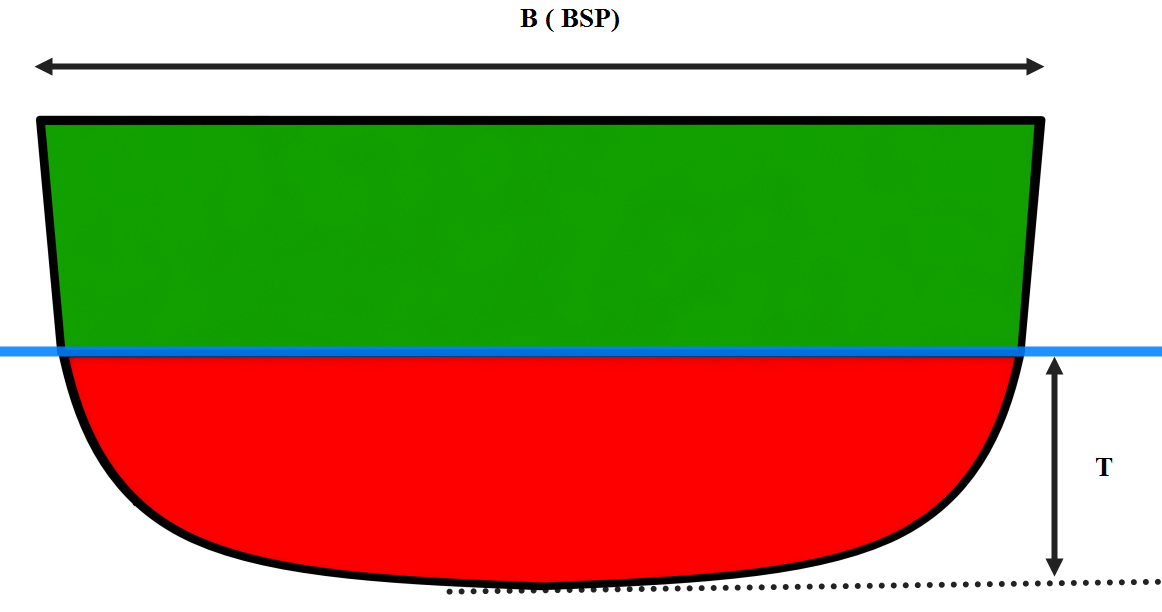
Figur 0110 viser Midtspant Koeffisient
Det røde viser midtspant arealet (Engelsk Area Midtship) under vannlinjen. Det grønne viser over vannlinjen og som fremhever BSP. CM vil bli det røde arealet dividert på rektangelet BSP x T. CM vil variere med dypgående for et og samme skip. Hvis man tar utgangspunkt i fullastet skip så vil et fyldig skip ha CM mellom 0,96 til 0,98, skarpere skip vil ha CM på 090 til 0,96.
Et skip har et midtspantareal (Am) på 172,5 m2.
Hva blir Cm når B = 20,4 m og T = 8,98 m?
CM = $\frac{\text{AM}}{B \times T}$ = 0, 94 (-). Et skip har CM = 0,979, B = 16 m og T = 7 m.
Hva er midtspant arealet?
CM = $\frac{\text{AM}}{B \times T}$ → Am = Cm × B × T = 0,979 × 16 m × 7 m = 109,648 m2
Prismatisk koeffisient (CP):
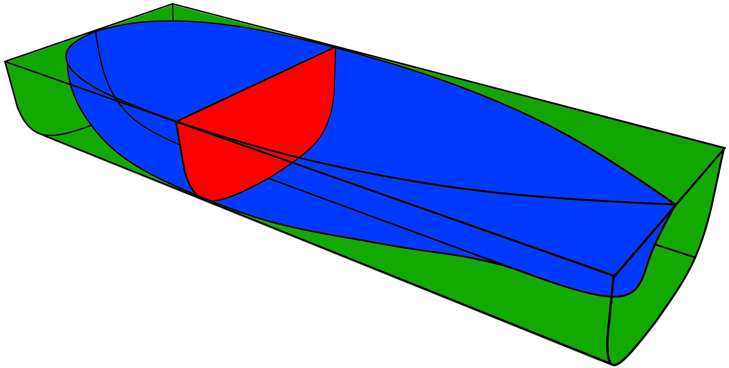
Figur 0111 Viser Prismatisk koeffisient
Det blå er volumdeplasement og det grønne er en rektangulær kasse som er like lang og bred og høy som volumdeplasementet (volum av skroget under vannlinjen). Det røde viser midtspant arealet (under vannlinjen). Hva er en prisme? Hvis man tar av den trekantede delen øverst på en melkekartong og lager et lokk på denne så det ser ut som en avlang eske, eller et prisme. Boksen som sjokoladen Toblerone ligger i kan være et annet eksempel på en prisme. CP gir en beskrivelse på skipets linjeføring mot endene, det vil si hvor fyldig volumdeplasementet er mot endene. Stor CP betyr at volumdeplasementet er fordelt forholdsvis mye mot skipets ender.. CP = $\frac{\nabla}{AM\ \times LPP}$. Man ser at CP har mye til felles med CB og CM, hvis man setter formelen opp slik:
CP = $\frac{\text{LPP x B x T x CB}}{\text{B x T x LPP x CM }}$
Hher kan man forkorte:
CP = $\frac{= (\text{ LPP}\text{ x }\text{B }\text{x }\text{ T}\text{ x CB }}{B\text{ x}\text{ T}\text{ x}\text{ LPP}\text{ x CM }}$ ,
så står man igjen med
CP = $\frac{\text{CB}}{\text{CM}}$ .
CP vil for en pram være lik CB men for et skip så vil CP alltid være større enn CB. Et skip med lengde på 102 m, bredde 14,5 m og har et volumdeplasement på 8980 m3.
Skipets dypgående er 7,3 m og CM for skipet er 0,98 (-).
Hva blir CP?
Beregner først CB = $\frac{\ \nabla}{\ L\ \times \ B\ \times \ T\ }$ = 8980 m3/ 102 m × 14,5 m × 7,3 m = 0,83. CP = CB/Cm =0,83/0,98 = 0,84 .
Kort oppsummert
CW = Forteller om formen på et bestemt vannlinjeplan
CB = Forteller om fyldigheten til volumdeplasementet
CM = Forteller om midtspantet finhets form
CP = Forteller om hvor fyldig volumdeplasementet er ut mot endene
Spring og Bjelkebukt:

Figur 0112 Viser spring og bjelkebukt
Spring: Er den vertikale høydeforskjellen (i rødt) mellom dekk i midtspantet og i skipets ender. Spring gir større fribord ved forre og aktre perpendikulære. Bjelkebukt er høydeforskjellen (grønt) i fra dekk i borde til dekk i senterlinjen (midt i mellom styrbord og babord side). Normalt er denne høydeforskjellen på B/50, der B er skipets bredde i meter. Bjelkebukt hjelper til at skipet kvitter med seg vann på dekk, i dag er det mange skip som bygges uten bjelkebukt på grunn av ønske om lettere konstruksjon.
Konstruksjonselementer til bunnseksjon:
Et skip består av mange konstruksjons elementer, her ser man hva som inngår til en dobbelbunnseksjon. En dobbelbunn har to funksjoner, som en sikkerhetsfaktor for et skip hvis det grunnstøtter og som en ballasttank med lavt tyngdepunkt for ballasten. Et skip blir utsatt for flere typer belastninger, det skal bære sin egen vekt, dynamiske belastninger når det beveger seg i sjøen (bølger), når det er last om bord og i tillegg trykkbelastninger av væske (saltvann). Jo lengre skipet er dess større belastninger vil det oppstå. Et skrog må stives av. Bunnstokken stiver av bunnen, er sveist til både kjølplaten og bunnplatene, Bunnstokkene er plassert tverrskips og forbindes med spantene (tverrskipsspant). Til å stive av mellom bunnstokker benyttes bærere, midtbærer (senterbærer) er plassert i senter på kjølplaten og står vinkelrett på bunnstokken. Sidebærer er plassert på siden av midtbæreren parallelt og jo flere jo bredere et skrog er. Ytterst i borde er slagbærer og den kan danne en begrensing på dobbelbunntanken utstrekning. Bærerne er kraftige bjelker, parallelt med bærene så er det stivere, disse er ikke så kraftige og det er ikke så lang avstand i mellom de som det er med bærene. På bunnstokkene er spantene sveiset og har som oppgave å stive av sideplatene (hudplater). Kjølplaten er i senter, bunnplatene er helt ut til kimingen, slagplate er den platen som er i kimingen (overgang fra bunn til skuteside) og der hvor platene er rette på skutesiden kalles for sideplater(hudplater).
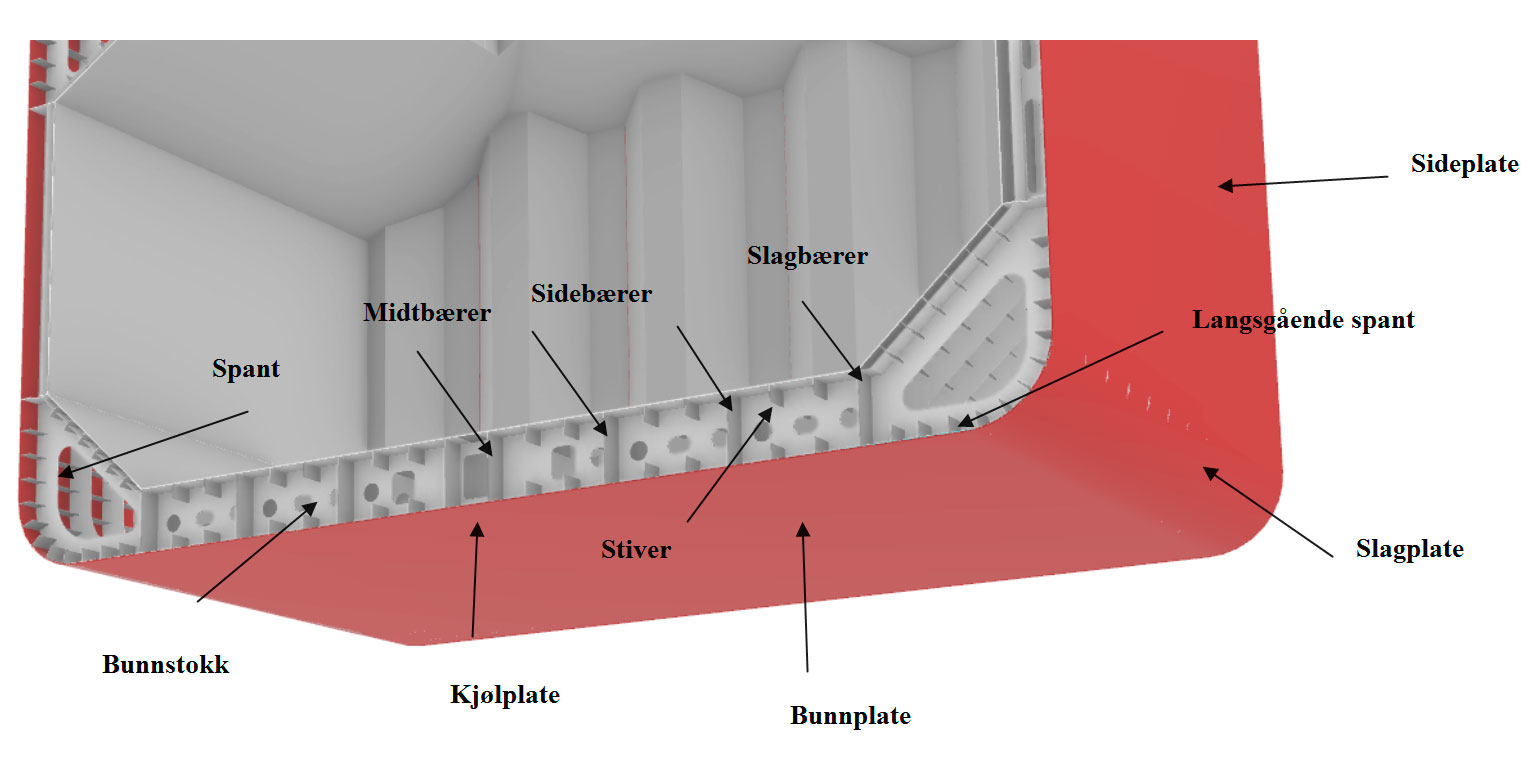
Figur 0113 viser konstruksjonselementene til en bunnseksjon
Vanntette tverrskipsskott:
Det er krav til stabilitet for skip også når det blir skadet, slik som i en kollisjon og for å unngå at skipet synker for lett er det inndelt i avdelinger. Det er flere typer avdelingskip, hvis skipet er av type 1- avdelingsskip så skal det tåle fylling i en avdeling uten å synke. En avdeling består av to vanntette tverrskipsskott i hver ende, borsett fra helt fremst eller akterst på skipet. Der fremste tverrskipsskottet kalles for kollisjonskottet. Dette skottet skal være plassert i en avstand fra forre perpendikulær på minst 0,05 L eller 10 m ( L = LPP) , det er den minste verdien som skal anvendes. Det er krav til vanntette tverrskipsskott i lasterommene og til maskinrommet, det skal monteres skott som skiller maskinrommet fra lasterom og rom i innredningen forut og akterut. På passasjerskip skal det også monteres et hylseskott.
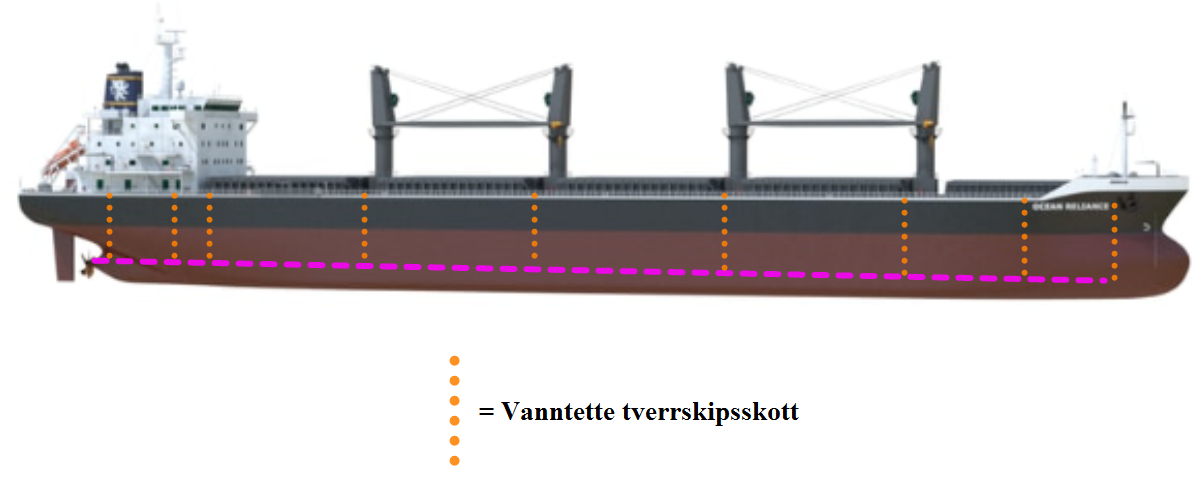
Figur 0114 viser et skip med illusterte vanntette tverrskipsskott
Fribords merke:
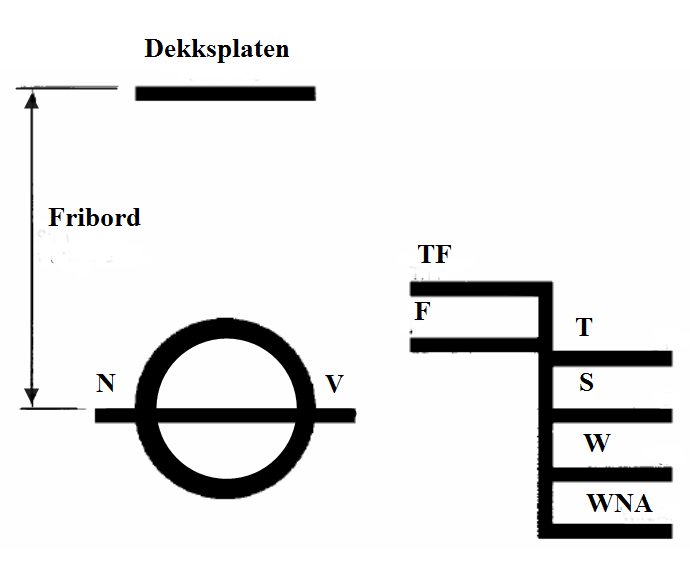
Figur 0115 Viser det internasjonale fribords merke.
Lastelinje-Konvensjonen
Den internasjonale lastelinjekonvensjonen ( International Convention on Load Lines) er en IMO-konvensjonen som gjelder for alle fartøy i internasjonal fart, med følgende unntak: skip i krig; skip på mindre enn 24 meters lengde; lystyachter som ikke er engasjert i handel; og fiskefartøy.
Den første internasjonale lastelinjekonvensjonen, som ble vedtatt i 1930, var basert på prinsippet om reststabilitet, selv om det var anerkjent at fribord også sikrer tilstrekkelig stabilitet og unngår overdreven stress på skipets skrog som følge av overbelastning. Reststabilitet er lukkete rom (volum) ovenfor vannlinjen.
I lastelinjekonvensjonen som vedtatt av IMO i 1966 avsettes det for å bestemme fribord av skip ved oppdeling og stabilitetsberegninger i skadet tilstand. Konvensjonen tar hensyn til de potensielle farene som finnes i forskjellige soner, områder og ulike årstider. Det tekniske vedlegget inneholder flere ekstra sikkerhetstiltak vedrørende dører, lenseporter, kummer og andre elementer. Hovedformålet med disse tiltakene er å sikre vanntetthet av skipsskrog under fribords dekk. Alle tildelte belastningslinjer skal merkes midtskips på hver side av skipet, sammen med dekkslinje. Skip beregnet for transport av tømmerlast er tildelt et mindre fribord som gir dekkslasten beskyttelse mot virkningen av bølger. Konvensjonen definerer maksimalt tillatte dypgang på et skip, og hvordan dette skal markeres på begge sidene av fartøyet.
Fribords merket
Definisjon av fribord er fra overkant av dekksplaten (dekkslinje) i bordet ved midtskipspantet og ned til overkant av lastevannlinjen. Denne er bestemt ut av krav til fartøystype, fartøyets lengde, styrke på romluker, høyde på bakk osv. og beregningene blir utført av et klasseselskap. Lastevannlinjen er den linjen som går horisontalt i gjennom senter av sirkelen.
På denne står initialene til klasseselskapet og NV står for Norske Veritas. Til høyre for sirkelen står en stamme med horisontale lastelinjer merker og der hvor det står S er Sommermerket. Den er i samme høyde som lastelinjen og gir flere betegnelser slik som: Sommerfribord, skipets sommerdypgående som igjen gir sommerdeplasement og sommer dødvekt. På figur 0106 så er sommerdypgående markert med en horisontal linje og sommerdypgående for Linda er 8,98 meter. Sommerdeplasement er 21441 Tonnes og sommer dødvekt er 16546 Tonnes. Opplysninger til et skip slik som dypgående, fribord deplasement, dødvekt og for et eksempel blokk koeffisient er som regel oppgitt ved sommerdypgående.
Det er flere merker, slik som vintermerket, tropemerket og for skip med lengde under 100 m er det et eget merke for vinter nord Atlanter (WNA, Winter North Atlantic). Av skipene som det jobbes med i skolesammenheng er det kun MS Mercandian Importer med sin 70.8 meter at WNA er gjeldene for. Alle de horisontale lastelinjer som er til høyre på stammen er for saltvann, de som er til venstre for stammene er for ferskvann.
Linda har lengde over 100 m og har det ikke men Mercandian Importer er 70 m lang og har det. Alle de horisontale lastelinjer som er til høyre på stammen er for saltvann, de som er til venstre for stammene er for ferskvann.
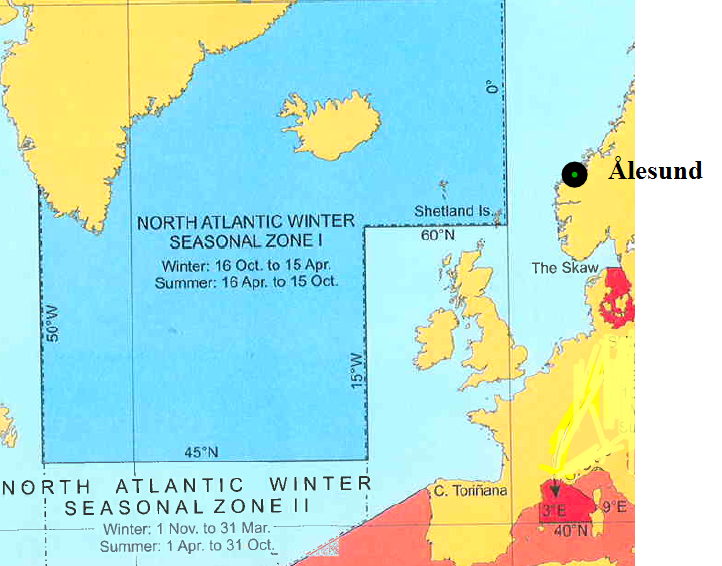
Figur 0116 viser Utsnitt av et sonekart
Ovenfor er et utsnitt i fra et sonekart og hvordan regelverket virker.? Hvis Linda ankommer Ålesund uten last den 02 november og skal laste så mye last som er tillat for denne årstiden. Ut fra kartet så ser man at Ålesund ligger i nord Atlanter vintersone II som er en sesongsone. Det vil si at fra 01 november til og med 31. mars så er det vintersone, fra 1. april til og med 31. oktober er det sommersone.
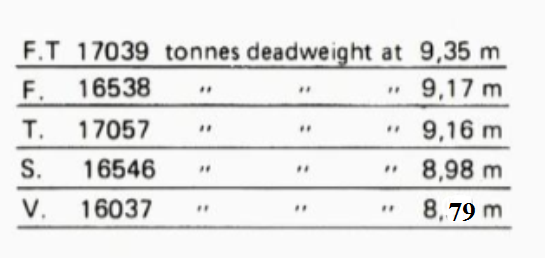
Figur 0117 Lastemerker til Linda ××
Så hvor mye kan Linda laste opp i Ålesund den 02. november? For lastemerket Vinter så er dødvekt 16037 Tonnes, dersom vekt av beholdning som: bunkers, ferskvann, reservedeler er på 1000 Tonnes så kan det lastes opp: 16037 Tonnes -- 1000 Tonnes = 15037 Tonnes. I nærheten av ekvator er det tropesone og der et tillat dødvekt 17057 Tonnes.
Tonnes pr cm immersion (TPC):
Immersion er Engelsk og betyr neddykking. Til høyre for dødvektkolonnen er TPC kolonnen og den forteller om hvor mye vekt som må lastes om bord for å få skipet til å dykke ned 1 cm. Til dypgående på 8,90 m så er TPC i saltvann på 27,61 Tonnes. Lengde og bredde av vannlinjeplanet vil variere med dypgående, vannlinjearealet vil øke med større dypgående og derfor er TPC større ved dypgående på 8.98 m enn på 5.50 m for MS Linda. For en pram som er rektangulær i form så vil vannlinjearealet være like stort for alle dypganger. En pram med mål: lengde 40 meter og bredde 15 meter.
Så blir AW: L × B × CW. 40 m × 15 m × 1 = 600 m2.
Hvis man lager en høyde på vannlinjearealet som er 1 cm, 1 cm = 0,01 m = 1/100 så blir volumet= 6 m3.× $\frac{1}{100}$ m = 6 m3 .
Vekten av volumet i saltvann blir volum × p = 6 m3 × 1,025 tonn/m3 = 6,15 Tonnes. TPC for denne prammen blir 6,15 tonn/cm.
Formel for TPC
Formel for TPC = $\frac{AW\ \times 1,025\ tonn/m3\ }{100}$ = Tonn/cm
Figur 0118 viser et Vannlinjeareal og volum med 1 cm høyde til vannlinjearealet.
Tyngdekraft og oppdriftkraft:
Fra fysikkens verden er g = 9,81 m/s2.
Tyngdekraft for et legeme er masse (kg) × g = Newton (N), oppdriftkraften vil bli for samme legemet: volum × p × g.
Disse vil være like stor men motsatt rettet. m × g = volum × p × g, → m × g = volum × p × g (forkorter bort g på begge sider).
For et skip så blir $\mathrm{\Delta}\ = \ \nabla\ $× p og benevnelsen blir Tonnes.
Hvis et skip har $\mathrm{\Delta}$ = 2000 Tonnes så blir oppdriftkraften = - 2000 Tonnes. $\mathrm{\Delta}$ ( vektdeplasement) virker i skipets felles tyngdepunkt G og $\nabla$ × p virket i skipets felles oppdriftspunktet B.
For en pram vil oppdriftspunktet B bestandig bli midt i mellom vannlinjen og underkant av K, som blir dypgang (T) / 2.
For et skip så blir formen på volumdeplasementet avgjørende hvor oppdriftspunktet vil plassere seg, for et skip med stor CB så vil B plassere seg i nærheten av T/2.
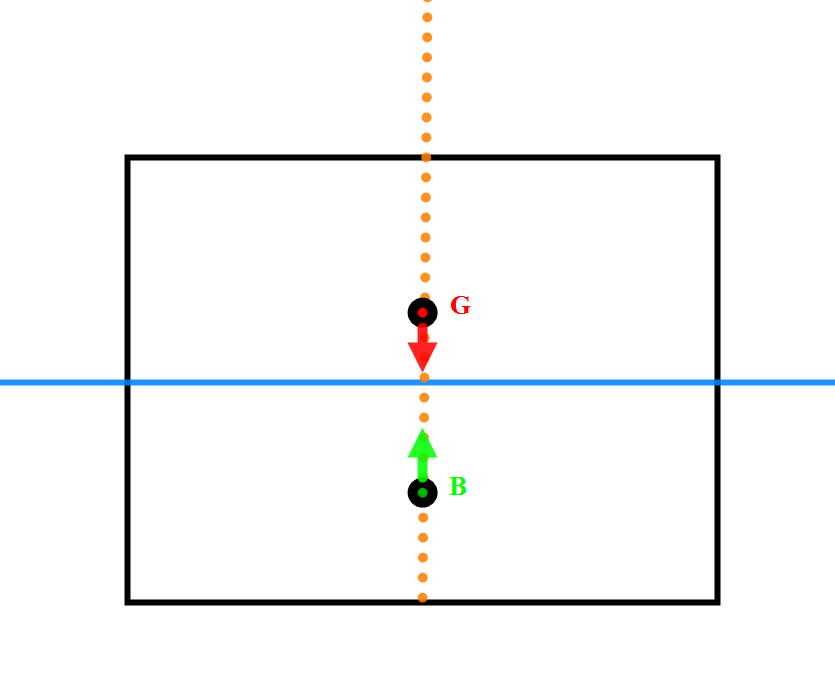
Figur 0119 viser en illustrasjon av tyngde og oppdriftkraft
Moment og fellestyngdepunkt:
Moment = kraft × arm, i fra fysikkens verden så vil det bli: m × g × arm men også her kan man forkorte bort g på begge sider da den virker både på skipet og på den gjenstand som lastes om bord.
Man står igjen med vekt × arm som da vil bli: tonn × arm = Tonnmeter (TM). Et tyngdepunkt kjennes ved at momentet i et tyngdepunkt er lik null. Det benytter man seg av hvis et bord skal forflyttes (løftes) av kun en person (se figur 0120). Hvor tar man tak på bordet? Jo på midten fordi der er tyngdepunktet og med null moment så er det lettest å forflytte. Vekten av bordet er den samme uansett hvor man tar tak .

Figur 0120 viser et stuebord
Tranverse metacenter above keel in meters (KM):
Tverrskips metasenter ovenfor K (kjølplate) i meter. Se Figur 0106 og på den kolonnen helt til høyre som kalles for KM. Den kolonnen oppgir hvor langt over K metasentret er plassert. Det er formen på volumdeplasementet som avgjør hvor langt over K metasentret vil bli. Hva er et metasenter? Se på skisse .... Her ligger skipet uten krengning og B befinner seg på senterlinjen. På skisse.. så krenger skipet til styrbord, den opprinnelige vannlinjen (stiplete linjen) og den nye vannlinjen skjærer hverandre på midten (senterlinjen) og danner to like store volumkiler. Dette medfører at det ikke blir økning eller forandring på volumdeplasementet størrelse. Når skipet krenger til styrbord så vil derimot B (oppdrift punkt) forandre posisjon. Det vil søke til styrbord, samme vei som krengningen og vil stille seg i midtpunktet til den nye formen til volumdeplasementet. Oppdriftkraften vil nå virke i B1, den vil være vertikalt og der hvor den skjærer senterlinjen med krengningsvinkel på 6 til 7 grader vil metasentret bli. Metasenter er et teoretisk punkt og blir benyttet til stabilitetsberegninger.
KM til Linda når T (dypgang) er 8,90 meter er lik 8,65 meter. For en pram så kan KM beregnes lett fordi en pram er rektangulær i sin form.
Formel for beregning er KM = KB + BM. En pram med mål: lengde 40 meter og bredde 15 meter og som har dypgang (T) på 5 meter.
Hva blir KM?
KB = $\frac{T}{2}$ = 2,5 m.BM beregnes etter formel: BM = $\frac{I}{\nabla}$ , hvor I er lik vannlinjearealets treghetsmoment .
Treghetsmomentet virker rundt midtlinjen i vannlinjeplanet og jo større treghetsmomentet er jo vanskeligere er det å påføre skipet en krengning. I beregnes etter formel:
$I = \frac{L\times B^3}{12}$ =
$\frac{40\ m\times\ 15m^3}{12}$ = 11250 m4 ( m3 × m = m4 )
Det divideres på 12 fordi det er en pram med rektangulær form, hvis det hadde vært et fartøy med form lik en trekant så hadde man dividert på 18.
$\nabla$ = L × B × T × CB = 40 m $\times \ $15 m $\times$ 5 m × 1 = 3000 m3. BM = $\frac{I}{\nabla}$ = $\frac{11250\ m^4}{3000\text{ ㎥}}$ = 3,75 m.
KM til prammen når den har T lik 5 m = KB + BM = 2,5 m + 3,75 m = 6,25 m. KM er et utrykk for formstabiliteten og B (bredde) har stor betydning for formstabiliteten. Jo større bredden er jo bedre er formstabiliteten.
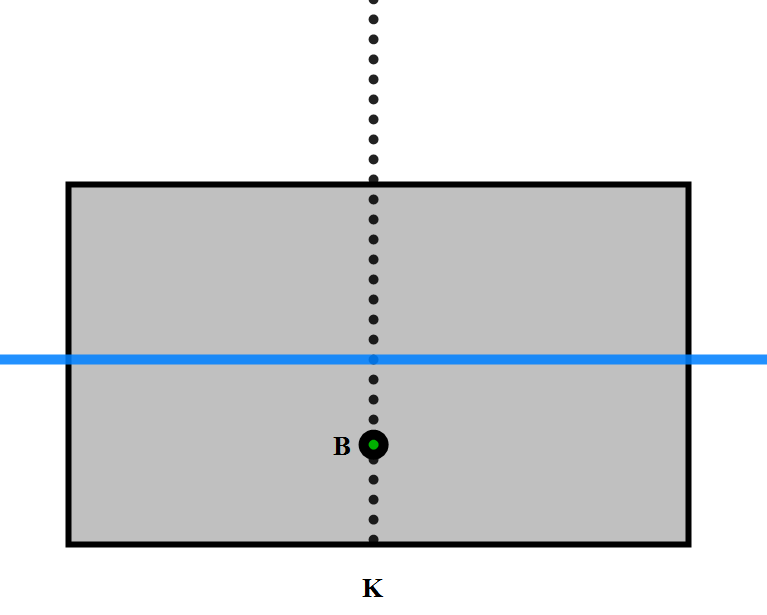
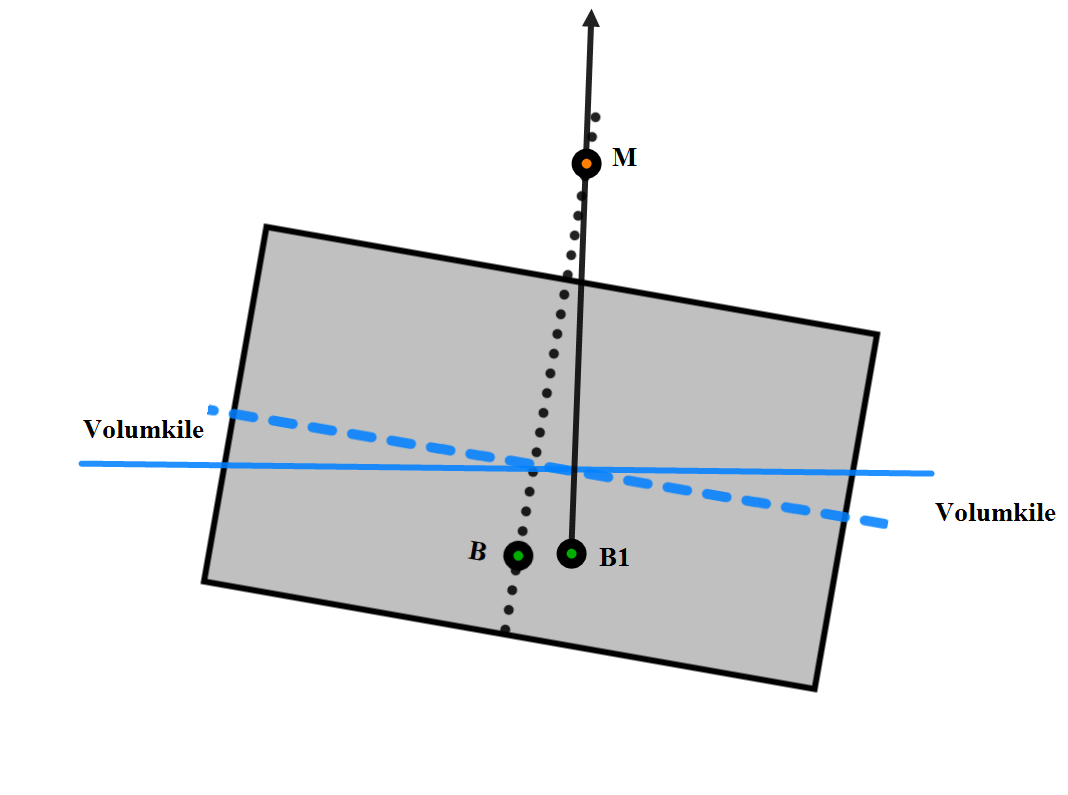
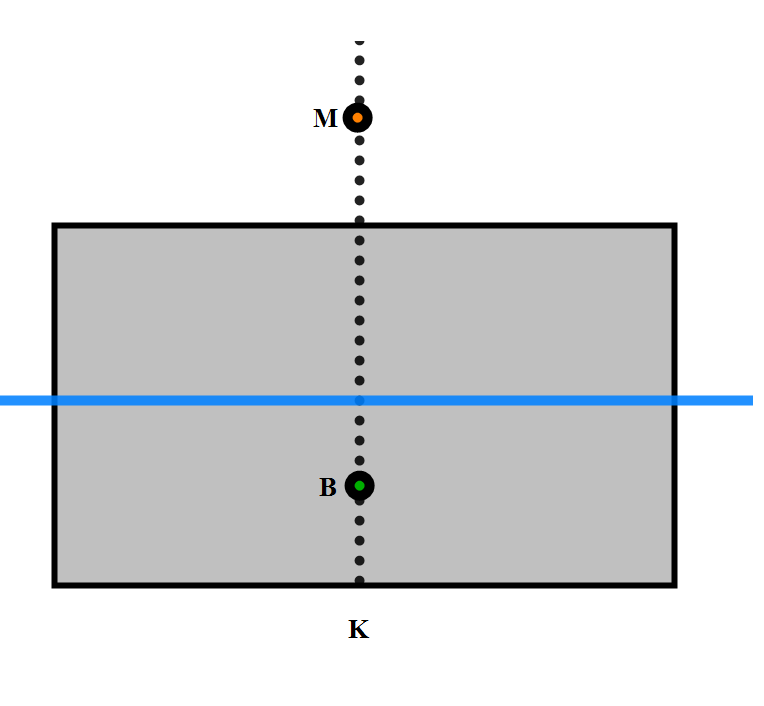
Figur 0121 viser 3 skisser som fremhever hvordan man beregner metasentre.
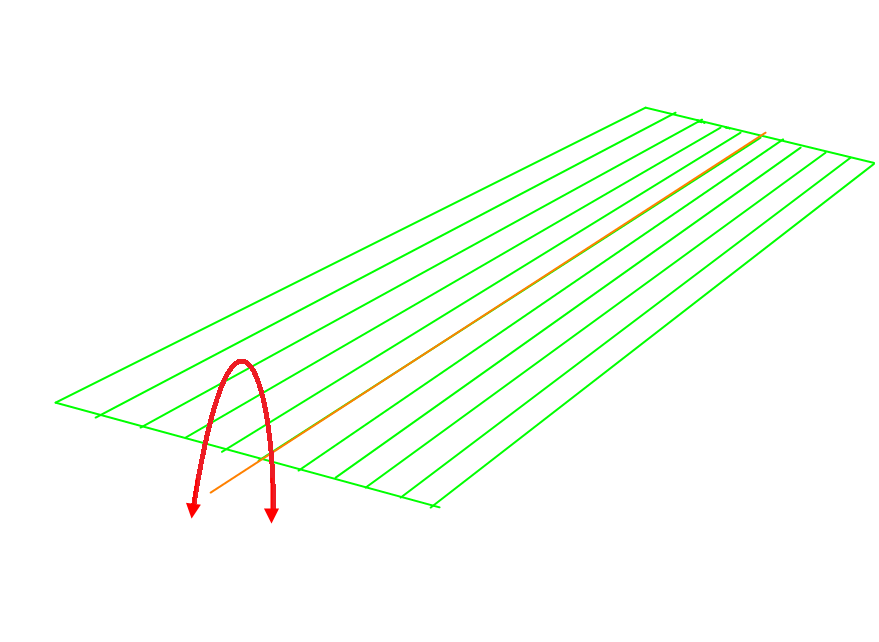
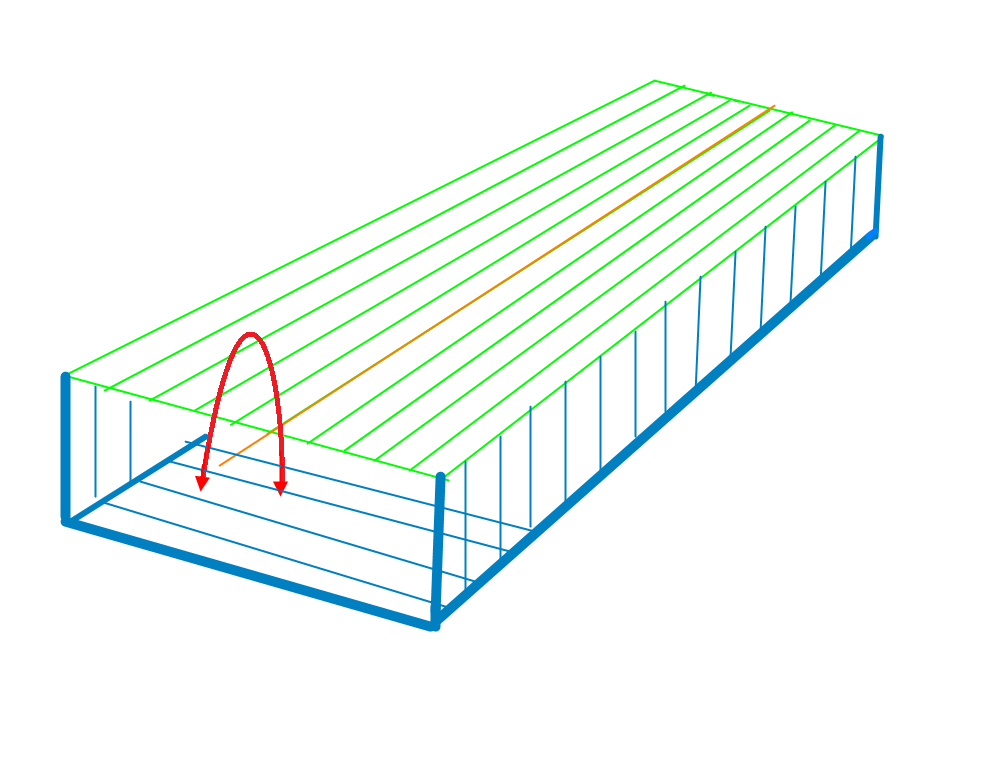
Figur 0122 Viser Vannlinjearealet treghetsmoment som virker rundt midtlinjen på vannlinjeplanet
Figur 0123 som viser en illustrasjon for BM = $\frac{I}{\nabla}$ (vannlinjetreghetsmoment dividert på volumdeplasement)
Vannlinjeplan /vannlinjeareal:
Vannlinjearealet er veldig viktig for stabiliteten. Hvis man sammenligner med hvor viktig gode dekk til en bil er for å oppnå kort stoppedistanse. En personbil på 1600 kg som har en hastighet på 80 km/timen. Den eneste kontakten med veibanen er med dekkene og som har et areal tilsvarende 4 postkort. Vannlinjetreghetsmoment er den mostand vannlinjeplanet gjør for å motsette seg krengning (rotasjon bevegelse om midtlinjeaksen). Jo større I er (m4) jo vanskeligere er det å påføre en krengning. Et vannlinjeplan har ikke noen tykkelse og ikke veier det noe heller men har stor betydning for skipets stabilitet. Når et skip får skade slik som i en kollisjon, så kan det medføre tap av vannlinjeareal og dermed forandring i BM fordi BM = $\frac{}{}$ og endringer i vannlinjeareal medfører endringer i I (treghetsmoment). Ved normale stabilitetsberegninger så tar man ut verdien KM i fra en plansje tilhørende skipet og benytter denne i beregningen uten å kanskje tenke på at vannlinjearealet inngår i denne hydrostatiske verdien.
I ( treghetsmoment) til et skip som Linda vil ha et tilnærmet I = $\frac{L\ \times \ \ \ B^{3}}{12} \times \ \frac{3}{4} $
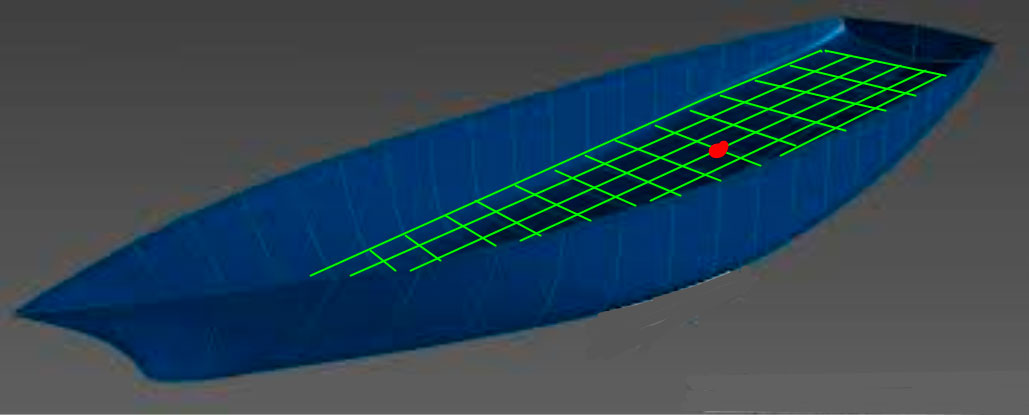
Figur 0124 Illustrerer et vannlinjeplan til et skrog som flyter i vann, der den røde prikken er tyngdepunktet til selve vannlinjearealet.
Linjetegninger (konstruksjonstegning):
Når skipets mål slik som LPP, B (BSP), Dybde i Riss og formkoeffisientene som: CB, CM, CP er bestemt så kan man gå i gang med å tegne skipet. En linjetegning viser skipets form, blir kalt for en projeksjonstegning og som i sitt plan, profil og snitt viser skipets linjer. I planen ses skipet ovenfra, i profilen fra siden og i snittet i fra endene.
Med hjelp av linjetegningen så kan volumdeplasementet beregnes.
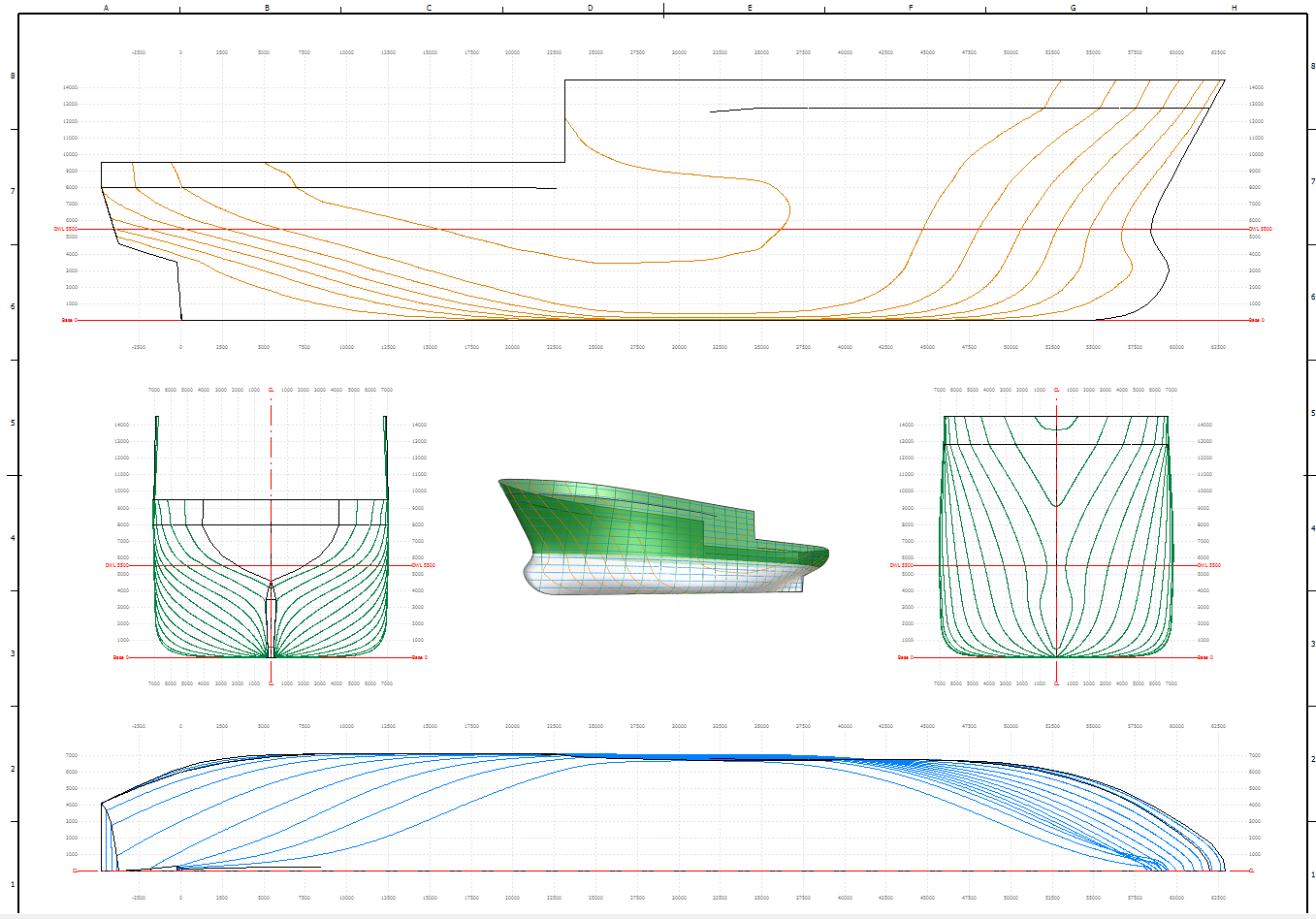
Fig0125.viser en linjetegning
Profil: (Øverst) Viser skroget sett fra siden med baugen til høyre. Skroget blir inndelt i flere langskipssnitt, disse har forskjellige avstand i fra senterlinjen (i bredde), normalt er det 5 langskipssnitt i tillegg til senterlinjesnittet. Overbygg, kran og lignende utelates i fra linjetegningene. Det er to referanser for lengdemål i meter, et over og et under, med utgangspunkt i aktre perpendikulær (nullpunkt). I vertikalt retning blir det vannlinjer med nullpunkt i bunnlinjen. Den røde horisontale linjen markerer en vannlinje og samme vannlinje er benyttet på snitt-tegningen som er på midten.
Spanteriss: (midten) er i to tegninger, den til venstre viser skroget sett aktenfra, den til høyre viser skroget sett forfra. I spanterisset tegnes spantene og dekkskonturene. I vertikalt retning vises vannlinjer og i horisontal retning vises bredden med nullpunkt i senterlinjen.
Vannlinjeplan: (nederst) Her er bare halve bredden tegnet og det er fordi skroget er symmetrisk om senterlinjen. Tegningen viser skroget sett under fra og med baug til høyre. I bredden kan også skrogets langskipssnitt tegnes inn men er ikke gjort det på denne tegningen.
Eldre Spanteriss tegning: Se figur. Her vises skroget kun sett aktenfra. Det til venstre for senterlinjen er spantene til akterskipet tegnet fra aktreperpendikulær til nullkrysspantet (midtspant), til høyre for senterlinjen er spantene til forskipet tegnet fra nullkrysspantet (midtspant til forstevnspant. Skipets LPP er delt inn i 10 like lange deler, det vil si for et skip med LPP på 150 meter så er en lengde lik 15 meter mellom spantene. Aktreperpendikulær er spant nummer 0 og forstevnspantet er nummer 10, i tillegg er det det halvspant og de blir tatt med der hvor skroget endrer seg mye i form i mellom 2 spant av de ordinære 11 spantene.
Til høyre for senterlinjen er det bakkdekk og til venstre er det hoveddekk.
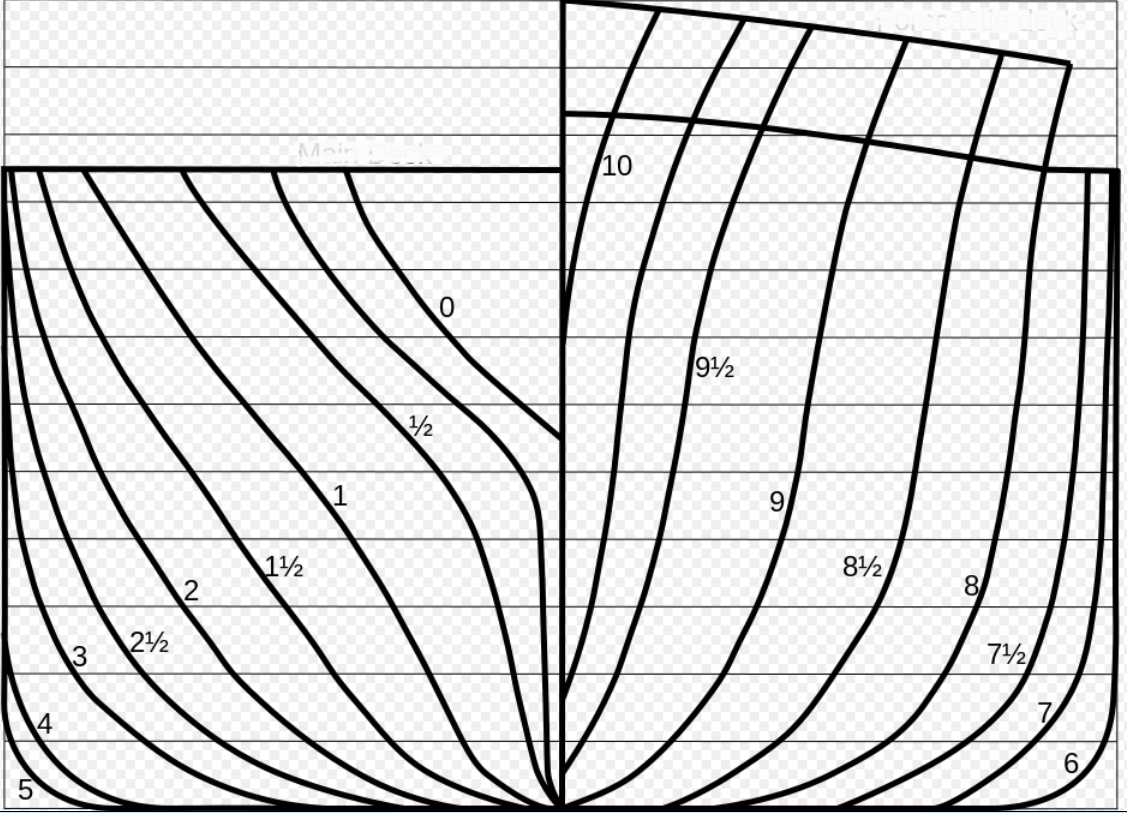
Figur 0126..viser en eldre spanteriss tegning
Målekonvensjonen 1969:
Målekonvensjonen ble vedtatt i 1969 og trådte i kraft i 1982. Den gir bestemmelser om hvordan et skips tonnasje og lengde skal beregnes. Både skipets netto- og bruttotonnasje skal beregnes. Konvensjonen gjelder for skip over 24 meter.
Etter at skipet er målt skal det utstedes et målebrev inneholdende nødvendige data om skipets mål. Konvensjonen avløste målekonvensjonen av 1947. Tonnasje, er et mål på lukkede rom på skipet målt på formlinjer (linjetegning), ofte brukt til størrelse av sertifikater for navigatører, mannskap størrelse (antall) og avgifter slik som havneavgift.
Bruttotonnasje, er et mål på de totale lukkede rom i et skip. Netto tonnasje, er et mål på rom som er nyttig for transport av last eller passasjerer. Tonnasje er ikke et uttrykk for vekt, men man kan lese i aviser om cruiseskip at bruttotonnasje er oppgitt som vekt og det bidrar til mange misforståelser. Brutto tonnasjen reflekterer størrelsen på skip, netto tonnasjen gjenspeiler kapasiteten til skip for å generer inntekter. I den tidligere målekonvensjon (1947) så var det benyttet betegnelsen brutto register tonn (BRT) og 1 BRT var 2,83 m3. BRT blir ikke benyttet i målekonvensjon 1969, hvor tilsvarende har en størrelse på nærmere 3 m3 men er tonet helt ned. Et brutto tonn (BT) har ingen benevnelse, for et skip som er målt til en brutto tonnasje på 500 så blir det oppgitt slik: BT = 500. Brutto tonnasje og netto tonnasje beregnes etter egne formler og resultatet fremkommer i et internasjonalt målebrev (International Tonnage certificate 1969). I et målebrev så må det fremkomme: Navn, Hjemsted, kjenningssignal, Brutto tonnasje og Netto tonnasje, byggested, byggenummer, byggeår, byggerens navn, størst lengde (LOA) også videre.
Et Rederi ønsker seg ikke skip som har stor bruttotonnasje hvis det kan unngås, fordi det gir økte havne og kanalutgifter. Et eksempel er LNG gasstanker, sammenligner to typer, den ene er Kverner (Moss) kuletanker og den andre er Membran tanker (Fransk) hvor tankene er integrert i selve skroget. Kuletanker egner seg bedre for frakting av LNG (Metan) men på grunn av større Brutto tonnasje velger rederiene heller å bygge membran tankere.
Transitt Suez kanalen
Det er en kostnad forskjell på 50 000 US dollar på å foreta en kanalpassering i Suezkanalen med en kuletanker og en mebramtanker.


Figur 0127 viser to LNG tankere, Kverner (Moss) kuletanker til venstre og Membran (Fransk) tanker til høyre.
Long ton og fotmerker:
Tidligere var det vanlig å oppgi deplasement, dødvekt og lettskip i long ton.
Long ton er Engelsk og 1 long ton er lik 1016 kg. Dypgangsmerkene var oppgitt i fot og derav betegnelsen fotmerker. En fot er 0,3048 m og en fot består av 12 tommer,12,5 fot vil bli 12 fot og 6 tommer.
M/S Simoa tilhørte Skibs-A/S Akersviken, Oslo, bygget i 1959 i Hamburg, Tyskland. Følgende data er kjent: Dødvekt: 14906 tons, lettskip: 5118 tons, LPP 491,9 fot, Bredde 66,6fot og Dypgang: 29' 07'' fot og tommer. Legg merke til at long ton betegnes kun som tons og må ikke forveksle med Tonnes. Hvis man skal beregne blokk koeffisienten til Simoa så må dataene omgjøres til Tonnes og meter først.
Dødvekt:15145,2 Tonnes og lettskip: 5200 Tonnes, Lpp: 149,93 m,
Bredde: 20,30 m og dypgang: 9,01m.
∆ = Dødvekt + Lettskip= 15145,2 Tonnes + 5200 Tonnes = 20345,20 Tonnes ,
$\nabla\ $= $\frac{\mathrm{\Delta}}{p}$ = $\ \frac{20345,20\ }{1,025\ tonn/m3}$ = 19849,0 m3.
Blokk-koeffisienten til Simoa blir:
CB= $\frac{\nabla}{L\ \times B\ \times \ T}\text{ }$ = $\frac{19208,6 m3}{149,93 m \times 20,30m \times 9,01\text{ m} }$ = 0, 72 (-)


Figur 0128 viser 2 bilder av Simoa
Motstand på skipet:
Ved beregninger/ bestemmelse av hoveddimensjoner (formkoeffisienter) til et skip i planleggingsfasen så er det flere hensyn en må ta.
Hva slags type last skal fraktes?
Fartsområder og seiling distanser?
Hvilke funksjoner skal skipet ha?
Hva vil man oppnå med skipet?
Det kan være lastekapasitet, nødvendig hastighet (knop), største lengde, bredde og dypgang? Linjeutformingen på et skip er viktig for hvor stor blir motstand, fartsegenskaper og hvor god blir stabiliteten? Hvis man ser på flere forhold med et skip, slik som L/B (lengde/bredde). Det vil ha stor betydning for mostand i vannet og hvilke egenskaper fartøyet har i sjøen. Et slankt skip vil ha mindre motstand men vil også ha reduserte sjøegenskaper. Forholdet B/T (bredde/dypgang) har stor betydning for stabiliteten til skipet. Et vanlig handelsfartøy vil ha B/T på omlag 2,5. Dypgangen (T) er beregnet / begrenset av seilingsområder som skipet er tenkt å seile i. Skal det seile til mange havner som har grunt havnebasseng? Det er laget en retningssnor for at T skal passe inn med følgende ligning:
$Dødvekt + Lettskip = L\ \times B\ \times T\ \times CB\ \times p$
Hher må man justere på T slik at ligningen samsvarer omtrentlig. En høy CB vil føre til høyere motstand på skipet. Det er viktig at linjene på skroget bør være myke og glatte uten brå overganger. Eventuelle brå overganger på linjene vil føre til økt motstand grunnet avløsninger (virveltilstand) rundt skroget. Slike avløsninger skjer ofte rundt akselbraketter, slingrekjøler, sidethrustere, og på skip med tverr hekk. Avløsninger skaper en etterstrømning som drar med seg vann bak det som forårsaker avløsning. Det er viktig at vannet skal kunne strømme uten hindring rundt og under skroget.
Når hoveddimensjonene til et skip er bestemt så er det lite en kan endre når man skal tegne linjer. Linjene til skroget vil ha betydning for motstanden, evne til å holde stø kurs og gode manøveregenskaper. Hensikten med å regne på hvor motstanden på et skip blir er for å kunne bestemme slepeeffekt og deretter motoreffekt og størrelse. Motstanden til et skrog kan bestemmes ganske nøyaktig ved å utføre en slepetest av en modell av skipet i en slepetank. Testing av modeller foregår som oftest i slepetanker, der modellen er festet til en vogn som sleper modellen i vannet..
Testing i slepetank en mest utbredte metoden, siden vognen klarer å slepe modellen med nøyaktig hastighet. William Froude var den første til å dele opp den totale motstanden til et skip. Han delte opp motstanden i restmotstand, friksjonsmotstand og luftmotstand. Da han studerte bølgemønsteret til modeller med like former i ulike hastigheter, fant Froude ut at bølgemønstrene hadde en geometrisk likhet når formene bevegde seg med hastigheter proporsjonalt kvadratroten av deres lengder. Proporsjonalt når to størrelser varierer slik at forholdet mellom størrelsene er konstant. Denne likheten mellom hastighetene har i senere tid blitt betegnet som Froude tall. Videre skulle han finne ut at restmotstanden for geometrisk like former var den samme. Det er nettopp denne vitenskapen som blir utnyttet for å forutsi et skips motstand i full skala. Fra tester utført på en skalert modell, kan man utnytte at rest motstand til modell og fullskala er lik. Man utnytter også at motstandskomponentene kan deles opp. Froudes tall (Fn) er gitt av formelen:
Froudes tall (Fn)
Fn = $\frac{V}{\sqrt{g \times \ L}}$
der V = hastighet , g = gravitasjonskonstant og L = skipets lengde.
Modelltesting foregår etter følgendeprosedyre:
- Måling av totalmotstand av skalert modell i korresponderende hastighet (Froude tall)
- Estimer friksjon-, form- og luftmotstand for modellen
- Trekk disse motstandskomponentene fra totalmotstanden for å finne restmotstanden (som er lik for modell og fullskala skip)
- Legg til de andre motstandskomponentene i fullskala for å finne total motstand for skipet.

Figur 0129 .iser en modell som blir slept i et basseng, etter en slepevogn som går på skinner, bassenget er utstyrt med bølegenerator.
Reynolds' tall:
Reynolds' tall: tall som beskriver strømningen i en væske eller en gass. Det er lik forholdet mellom væskens (gassens) kinetiske energi og det indre friksjonsarbeid, som henger sammen med viskositeten. Viskositet er et mål for hvor tyktflytende eller tyntflytende en væske er, væsker med lav viskositet flyter lettere enn væsker med høy viskositet, viskositet er en væskes evne til å motstå strømning.
Kinematisk viskositet
Kinematisk viskositet: 𝜈 = $\frac{\mu}{\rho}$ , som er viskositet dividert på tetthet.
Kinematisk viskositet er hvor fort væsken sprer seg i forhold til dens masse når væsken helles utover en flate.
Ved en viss verdi for Reynolds' tall går strømningen over fra å være laminær til å bli turbulent. Laminær strømning er en væskestrøm der alle partikler i væsken har samme hastighet, i motsetning til en turbulent strømning der de forskjellige væskepartiklene har ulik hastighet og retning. Ved turbulent strømming øker friksjonen i væsken til det mangedobbelte. Den hastighet dette inntreffer ved, kalles kritisk hastighet. Reynoldstallet: RN er en dimensjonssløs parameter som beskriver om en strømning er turbulent eller laminær langs en flate. En høy verdi for RN viser til en turbulent strøm. Kjennskap til Reynolds\' tall er viktig ved overføring av resultater som er oppnådd ved forsøk med små modeller til modeller i full størrelse, som for eksempel vindtunnelprøver med modeller til fly i full målestokk eller modeller i slepetank til skip i full målestokk. Det oppstår mostand når et skip generer bølger i det vannet det beveger seg i. Det er denne mostanden man kan påvirke i størst grad på et skip ved å forme skroget slik at mengden av bølger som dannes reduseres.
Bulbbaug:
Ved å montere en bulb på et skip så vil en som regel få bedre motstandsegenskaper. En bulb vil lage et bølgesystem i motfase med skrogets eget bølgesystem. Dette vil gjøre den totale bølgen mindre enn den originalt ville vært og dette reduserer motstanden. Mulig å få opptil 20 % reduksjon i motstand som vil medføre besparelse i drivstofforbruk. Figur viser et ideelt resultat.
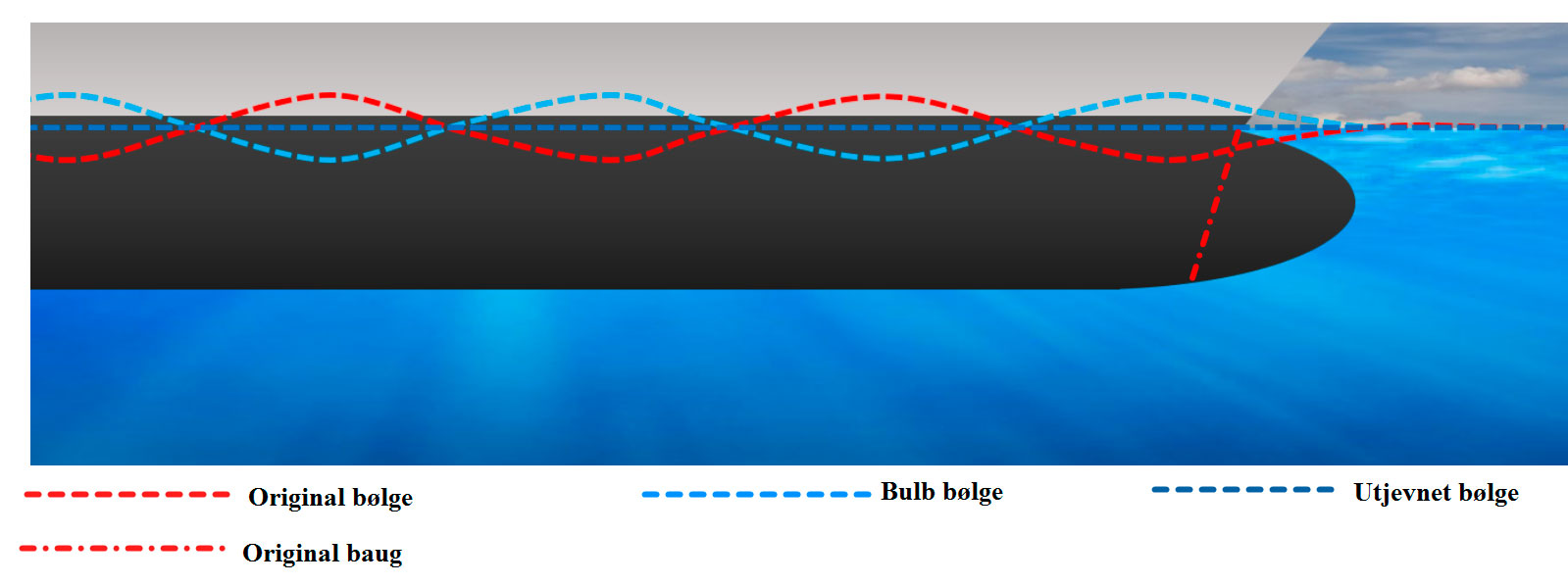
Figur 0130 Bulbbaug
Luftmotstand:
Forårsaket av skroget ovenfor vannlinjen sin størrelse og utforming, det samme med overbygg. Luftmotstanden er et resultat av skipets egen hastighet og som virker konstant uansett hvor høyt det er på skipet.
Ruhetsmotstanden:
Våtoverflate er den del av skroget som er under vannlinjen ved sommerdeplasement og oppgis i areal (m2). Arealet kan være betydelig, for et stort tankskip kan våt overflate være på 25 000 m2. Ruhet er ujevnheter og som vil øke friksjonen med sine omgivelser enn hva det gjør når det er glatt. Ruhet skyldes begroing, skade i malingsbelegget, rust og gir et tillegg på friksjonsmotstanden. Skjellvekster kan gi betydelig økning og dermed økte driftsutgifter på grunn av mer forbruk av bunkers.
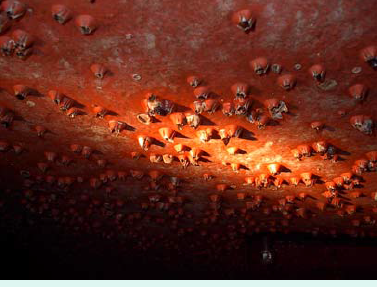
Figur 0131 viser skjellvokst bunns på et skip.
Prosjekt øket bredde: Stykkgodsskipet «Utgangspunkt Harmoni» vil bli benyttet som referanse når srykkgodsskipet «prosjekt 1» skal planlegges.
| Utgangspunkt Harmoni | Hoveddimensjoner |
|---|---|
| Deplasement | 17015 Tonnes |
| Lpp | 142 m |
| B | 18,60 m |
| Dybde i Riss | 11,75 m |
| T | 9,03 m |
| TPC | 22,10 Tonn pr cm |
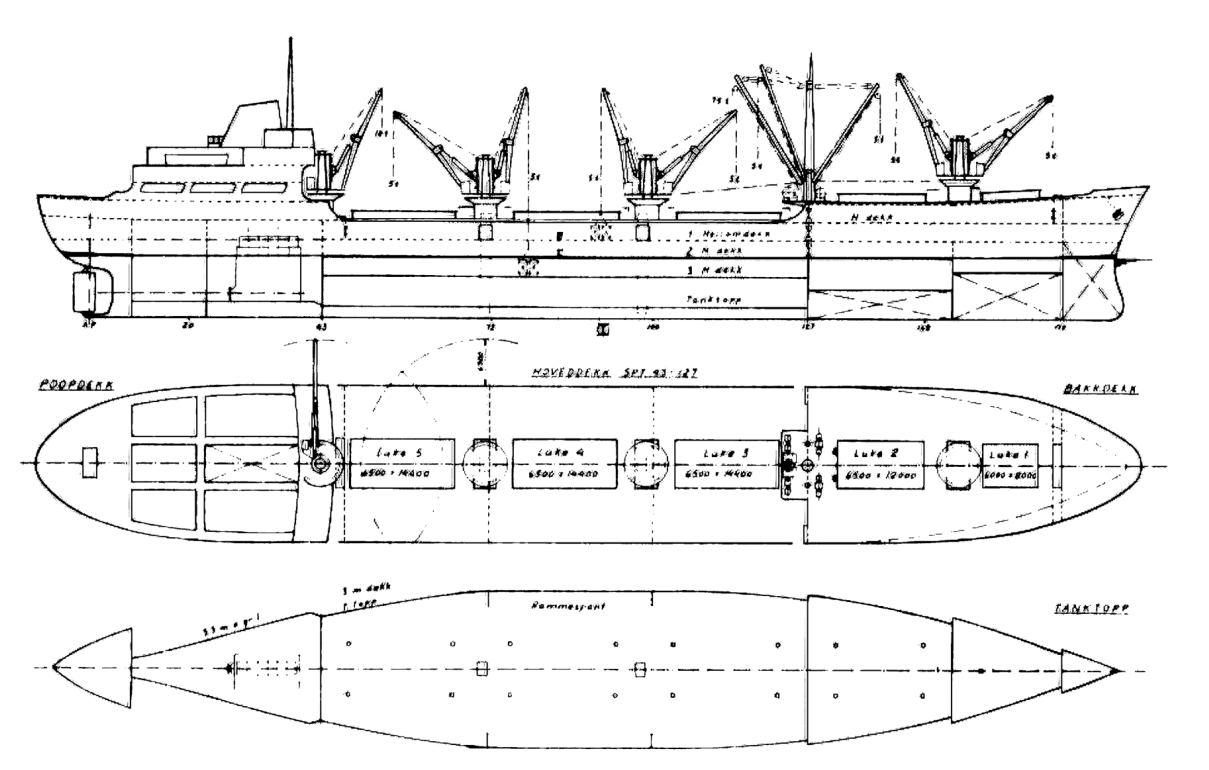
Figur 0132 Viser 3 skisser av «Utgangspunkt Harmoni»
Første oppgave blir å beregne CB og CW.
CB = $\frac{\nabla}{L\ \times B\ \times \ T}$ =$\frac{16600\ m^3}{142\ m\ \times \ 18,\ 60\ m\ \times \ 9,\ 03\ m\ }$ = 0,697 (-)
CW = $\frac{\text{AW}}{L \times B}$ men AW er ikke oppgitt?
Hvordan kan man beregne CW da?
Formel for TPC= $\frac{AW\ \times \ }{100}1,025\frac{\text{tonn}}{m3}$ ,
da vil et uttrykk for AW bli = $\ \frac{TPC\ \times \ 100\ \ }{1,025\ tomnn/m3}$ = $\frac{\ 22,10\frac{\text{tonn}}{\text{cm}} \times 100 }{1,025 tomnn/m3}$ = AW = 2156 m2
CW = $\frac{\text{AW}}{L \times B}$ = $\frac{2156 m^2 }{142 m \times 18, 60 m}$ = 0,817(-)
Srykkgodsskipet «prosjekt 1» skal øke sin lastekapasitet med omlag 30 %. LPP skal beholdes men det blir økning i Dybde i riss med 1,45 m og bredden med 2,8 m.
| Prosjekt 1 | Nye hoveddimensjoner |
|---|---|
| LPP | 142 m |
| B1 | 21,4 m |
| Dybde i Riss 1 | 13,2 m |
Bredden økes proporsjonalt overalt slik at CB blir uforandret og CW betraktes som det samme. På grunn av bredde økning vil T (dypgang) bli redusert.
Setter opp en ligning som betrakter volumendringen på begge sider av likhetstegnet. Økning i bredde i er 2,8 m/18,60 m = 0,15
δ T × L × B1 × CW = L × B × T × CB × δ B/B
δ T = T × CB × δ B / B1 × CW = 9,03 m × 0,697 (-) × 2,8 m / 21,4 m × 0,817 (-)
δ T = 1,00 m
TPC til Prosjekt 1 blir = 22,10 Tonn/cm × 21,4 m /18,60 m = 25,42 Tonn/cm.
Prosjekt 1: Det er antatt at vektøkningen blir på 800 Tonnes.
Hva blir T til Prosjekt1?
T Prosjekt1= T - δ T + 800 Tonnes/ TPC = 9,03 m - 1,00 m + 0,31 m = 8,34 m
| Prosjekt 1 | Hoveddimensjoner |
|---|---|
| Deplasement | 17815 Tonnes |
| Lpp | 142 m |
| B | 21,40 m |
| Dybde i Riss | 13,20 m |
| T | 8,34 m |
| TPC | 25,42 Tonn pr cm |
Hvis stykkgodsskip «Utgangspunkt Harmoni» gjorde 16 knop fart på sin prøvetur og det er ønskelig at «Prosjekt 1» skal også holde 16 knop så må det økes maskinkraften slik at denne blir lik økningen i slepehestekrefter ved 16 knop. (resultat i slepetank).
Areal: Beregning av et areal på en rektangulær flate utføres etter formel: Lengde × Bredde. Hvis lengden er 12 meter og bredden er 4 meter så blir areal = 12 m × 4 m = 48 m2
Figur 0133 rektangulær flate
Hvis man tegner en strek fra nedre venstre hjørne til høyre øvre hjørne så vil rektangelet bli til 2 trekanter. B (bredde) er byttet ut med H(høyde) og man ser lett at arealet for en av trekantene er halve arealet til rektangelet. Formel for areal til en trekant er: ½ × L × H = 0,5 × 12 m × 4 m = 24 m2
Figur 0134 viser 2 trekanter
Beregning av Areal ved hjelp av Simpson formel:
Figur 0135 viser en planskisse til et rom og her kan man ikke bruke noen av de formler ovenfor fordi den ene veggen har form som en parabel.. Det skal kjøpes inn maling til golvet og 1 liter maling dekker 6,85 m2.
Hvor mye maling må kjøpes inn?
Først må man beregne arealet av golvet og det gjøres med hjelp av Simpson formel. Hvis man betrakter tegningen slik at den består av tre linjer, en horisontal, en vertikal og en parabel. Den horisontale er oppgitt til å være 30 meter og antall ruter er 15.
Da blir en rute 2 meter, det samme forholdet gjelder også for den vertikale linjen.
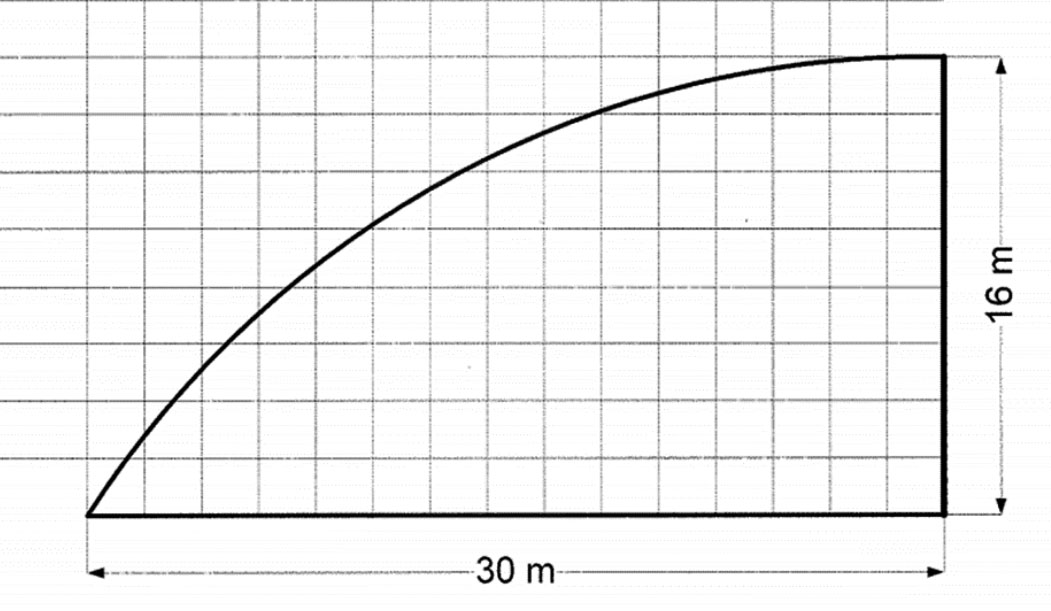
Figur 0135 viser en plan tegning av et rom.
Det tegnes inn ordinater, ordinatene er de røde vertikale pilene og nr. 1 starter på 0 meter. Ordinatene tegnes fra den horisontale linjen og helt til de berører parabelen, antall ordinater må være et oddetall. Jo flere ordinater jo mer nøyaktig beregnes arealet. Tegner inn 7 ordinater og da blir det 6 ordinater, det er krav til avstand mellom ordinatene må være like stor. Den horisontale linjen er 30 meter lang og det er 6 mellomrom, da blir avstand i mellom ordinatene 5 meter.
Mellomrommene blir a på tegningen a = 5 meter, 5 meter blir 2,5 ruter.
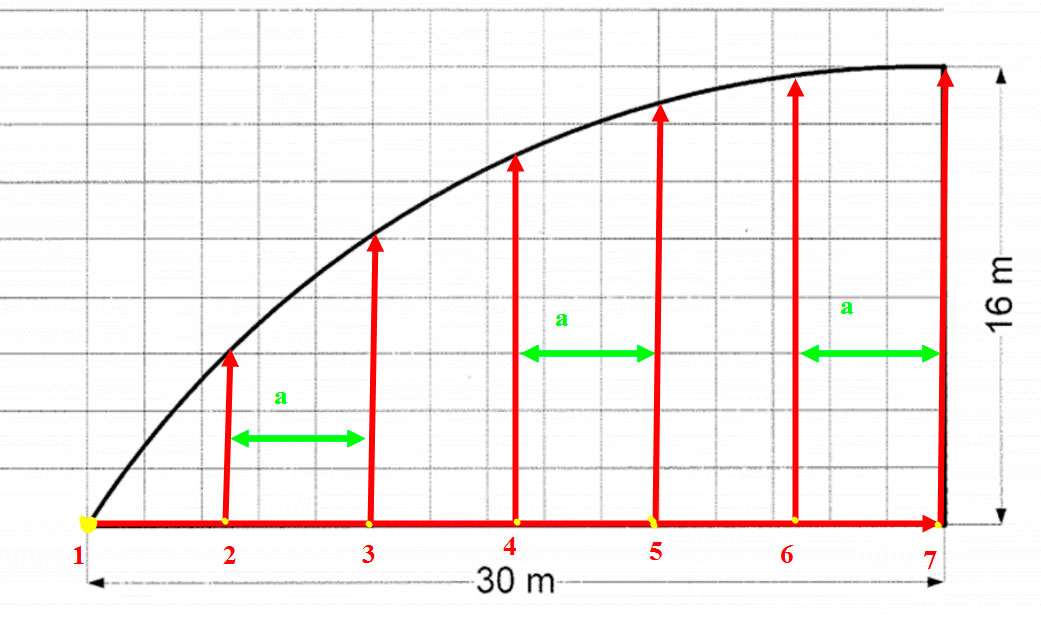
Figur 0136 viser 7 ordinater tegnet på plantegningen.
Neste trinn er å måle hvor lang hvert ordinat er. Den horisontale linjen er null-linjen og lengden måles ut i fra den vertikale linjen. Ordinat nummer 1 måles som 0 og ordinat nummer 7 måles som 16 meter.
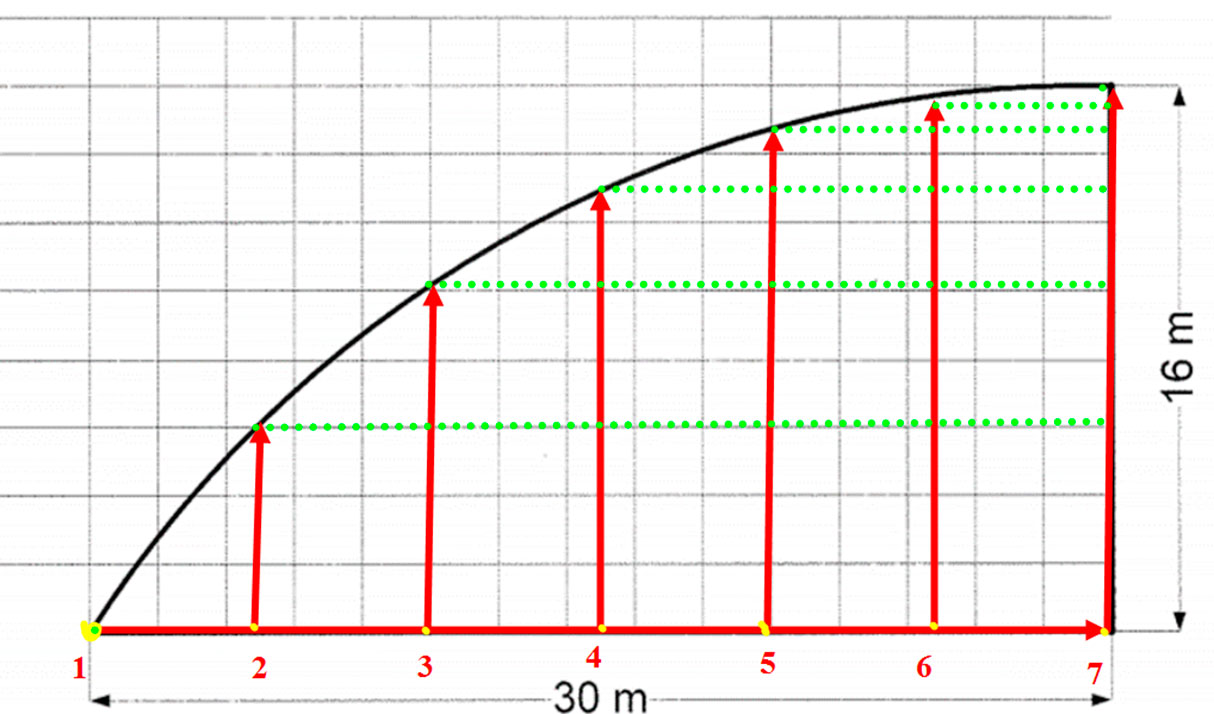
Figur 0137 viser hvordan man måler lengden til ordinatene
Lager til en tabell med fire kolonner og tilstrekkelig med rader. I den første kolonnen er det ordinatene som skal føres inn etter nummer. I den andre kolonnen føres inn den lengden som er målt til hver av ordinatene. Den tredje kolonnen føres inn Simpson faktor (SF) og den startet alltid med 1 og avsluttes med 1. Minimum antall ordinater er 3 stykker og da blir SF slik: 1- 4 -1, er det flere slik som her med 7 stykker så blir det et 2 tall etter 4, 4 tallet er alltid som nummer to og nest sist. Siste kolonner er det produkt, produkt er i matematikken et resultatet av en multiplikasjon. Her multipliseres ordinat lengde (meter) med SF (som er benevnelses løs ) og produkt får benevningen meter. Nederst i denne kolonnen summeres alle produktene.
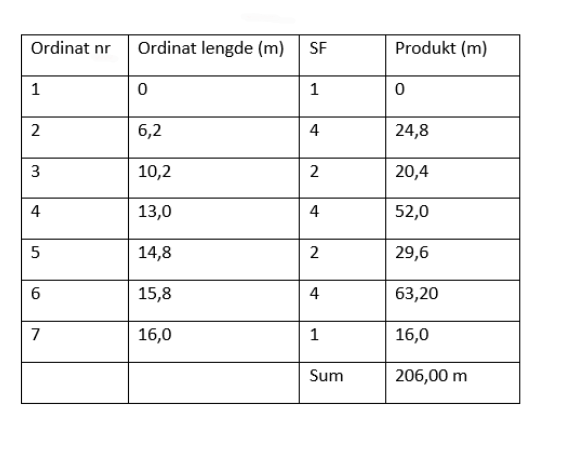
Figur 0138 viser en tabell for beregning av sum produkt
Formel for utregningen av arealet
Sum produkter × a /3, a i dette tilfellet er 5 m og 3 er en fast konstant.
Areal = $\frac{Sum\ produkter\ \times \ a}{3}$ = $\frac{206\ m\ \ \times 5\ m\ }{3}$ = 343,3 m2.
Hvor mange liter med maling må kjøpes inn?
Antall liter = $\frac{\text{Areal }}{liter/m2}$ = $\frac{343,3 m2 }{6,85 liter/m2}$ = 50,1 Liter ≈ 50 liter.
Vannlinjeareal med Simpson Formel:
Simpson formel egner seg godt til å beregne AW., men da beregnet man arealet av halvspant og multipliserer med 2 for å få hele vannlinjearealet.
Oppgave
Beregn AW og CW for skip i figur 0139..
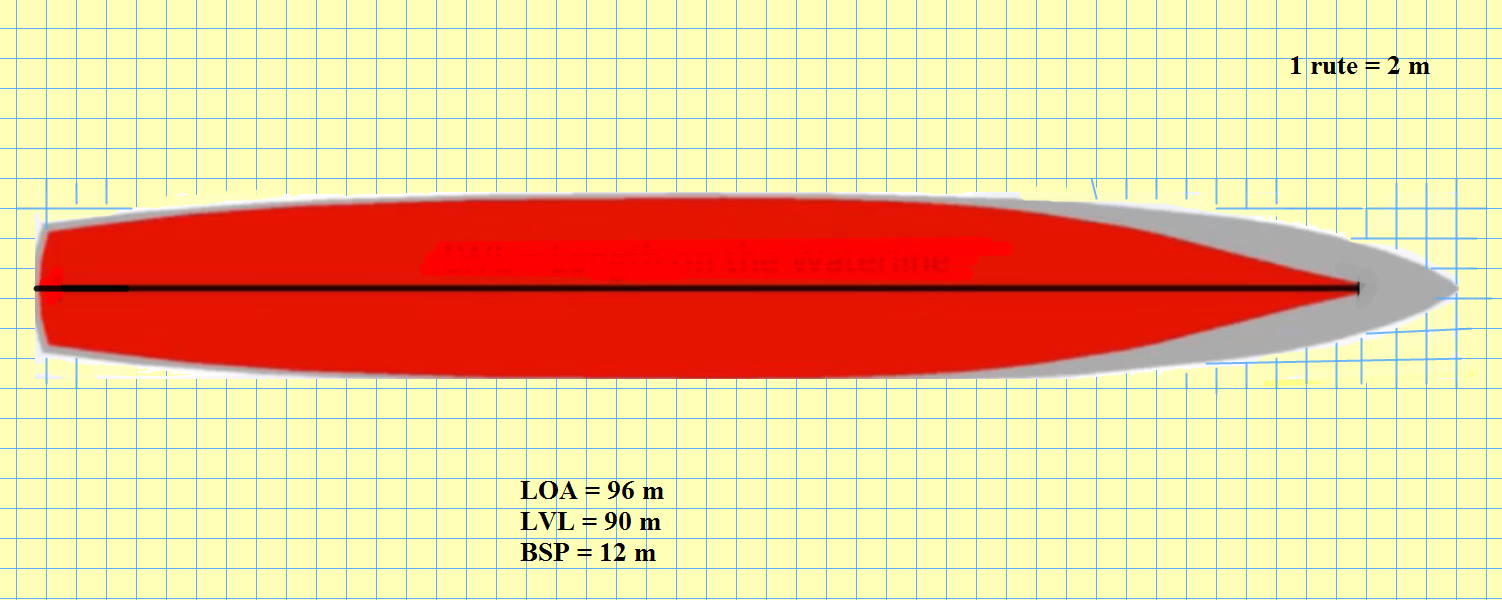
Figur 0139
LVL = 90 meter, med 7 ordinat så blir a = 90 m / 6 = 15 meter.
Starter bak og går fremover.
| Ordinat nr. | Ordinat lengde (m) | SF | Produkt (m) |
|---|---|---|---|
| 1 | 3,40 | 1 | 3,4 |
| 2 | 4,8 | 4 | 19,2 |
| 3 | 5,8 | 2 | 11,6 |
| 4 | 6,0 | 4 | 24,0 |
| 5 | 5,8 | 2 | 11,6 |
| 6 | 3,6 | 4 | 14,4 |
| 7 | 0 | 1 | 0 |
| Sum | 84,2 |
Areal = $\frac{\text{Sum} \text{produkter} \times a}{3}$ = $\frac{84,2 m \times 15 m}{3}$ = 421 m2.
AW = 2 × areal = 2 × 421 m2 = 842 m2..
CW = AW /LVL × BSP = 842 m2 / 90 m × 12 m = 0, 78 (-)
Beregning av LCF (tyngdepunkt til vannlinjearealet). Beregnes ved først å multiplisere produkt med arm i fra akterkant av vannlinjeplanet (ordinat nr. 1) til det aktuell ordinat som da blir Areal moment (m2). Arm i fra akterkant til tyngdepunktet beregnes ved å dividere sum Arealmoment med sum produkt.
| Ordinat nr. | Ordinat lengde (m) | SF | Produkt (m) | Arm (m) Fra AP ( akterkant) |
Areal moment m2 |
|---|---|---|---|---|---|
| 1 | 3,40 | 1 | 3,4 | 0 | 0 |
| 2 | 4,8 | 4 | 19,2 | 15 | 288,0 |
| 3 | 5,8 | 2 | 11,6 | 30 | 348,0 |
| 4 | 6,0 | 4 | 24,0 | 45 | 1080,0 |
| 5 | 5,8 | 2 | 11,6 | 60 | 696,0 |
| 6 | 3,6 | 4 | 14,4 | 75 | 1080,0 |
| 7 | 0 | 1 | 0 | 90 | 0 |
| Sum | 84,2 | 3492,0 |
Arm i fra akterkant til tyngdepunktet:
Areal moment /sum produkt = 3492, 0 m2 / 84, 2 m = 41, 47 m
LCF blir angitt i fra nullkryss-spantet (midtspantet) som er her 45 m i fra akterkant. LCF angis om den er akterlig eller forlig i forhold til nullkryss-spantet. I dette tilfelle så blir LCF: 3,53 m akterlig.
Tilleggs Oppgave Simpson formel.
Det er totalt 30 stk. elefanter langs X aksen og 80 m langs Y aksen.
Se figur 0140.
Beregn areal etter Simpson formel.
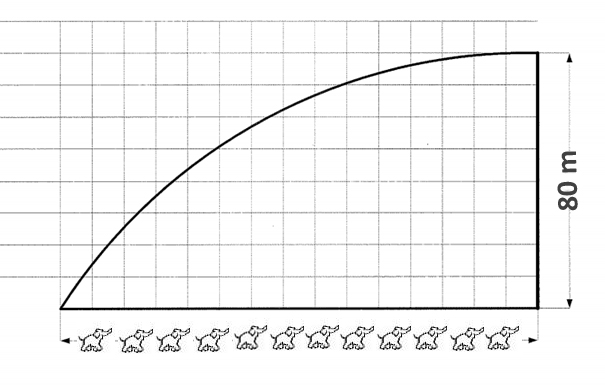
Figur 0140 Viser en planskisse med elefanter og meter.
Løsningsforslag:
| Ordinat nr. | Ordinat lengde (m) | SF | Produkt (m) |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
| 2 | 29,5 | 4 | 118 |
| 3 | 50,4 | 2 | 100,8 |
| 4 | 64 | 4 | 256 |
| 5 | 73 | 2 | 146 |
| 6 | 79,5 | 4 | 318 |
| 7 | 80 | 1 | 80 |
| Sum = | 1018,8 |
Areal = $\frac{sum\ produkter\ \times \ a\ }{3\ }$ =$\frac{\ \ 1018,8\ m\ \times \ \ 5\ elefanter\ \text{ }}{3 }$ = 1698 meterelefanter

