2. Tverrskipsstabilitet
$\require{cancel}$
Læremål:
Studentene skal ha kompetanse som gjør dem skikket til å vurdere og opprettholde skipets sjødyktighet, herav:
- Kunne forklare statisk og initial stabilitet
- Forflytting av tyngdepunkt, samt planlegging og justering av skipets KG ved lasting, lossing og flytting av vekter.
- Beregne og tegne stabilitetskurver, og arealet under disse
- Kunne forklare og beregne fri væskeoverflate i en tank
- Effekt av slakke tanker på skipets stabilitet
- Kunne vurdere skipets stabilitet opp mot regelverket
- Kunne bruke lasteroms- og tankkapasitetstabeller
- Angle of Loll
Undringsoppgaver:
- Har du noen gang tenkt over hva som gjør et fartøy stabilt?
- Hva tror du ligger i begrepet stabilitet?
- Tenk på fartøy du har vært på, hvordan bevegelsene i dårlig vær vært? Kan du tenke deg hvorfor det var slik?
Vi deler inn stabilitet i tre deler, tverrskips- og langskipsstabilitet, og krengning.
I dette kapittelet skal vi fokusere på tverrskipsstabilitet. Men man vil alltid ta hensyn til stabiliteten i alle tre retninger når man er ute på et fartøy.
Stabiliteten tverrskips defineres som «Et skips evne til å forbli i opprettstilling eller til å gjeninnta en slik stilling når det krenges over av en ytre påvirkning, som vind eller sjøgang».
Et skip med dårlig tverrskipsstabilitet kan lett kantre, selv i stille vær. For stor stabilitet kan medføre store påkjenninger for folkene om bord, og den kan oppstå skader på skip og last. Skipsbyggeren må sikre at skipet har tilstrekkelig stabilitet, ikke for stor og ikke for liten.
Hvordan stabiliteten til et fartøy er, avhenger mye av hvilken type skip det er. Er det et containerfartøy som har lasten høyt plassert på dekk? Eller er det en tankbåt med lasten plassert under dekk i lastetanker?
Det er to hovedtyper stabilitet, og det er «formstabilitet» og «Vektstabilitet».
Formstabilitet
Formen til et fartøy varierer veldig hva hvilken type fartøy det er. Her er det formen i tverrskips retning som har betydning. Er det et bredt fartøy, med en fyldig skrogform under vannlinjen på grunn av lastetanker? Er det en katamaran? Eller er det et smalt containerskip?
Typiske skip med en smal skrogform
Typiske skip med en smal skrogform er: Cruiseskip, containerskip, fregatter, seilbåter
Disse fartøyene er bygd for å ha lite motstand, slik at fartøyet kan holde en høy hastighet. Disse fartøyene har lave koeffisienter (Cb, Cw, Cm, Cp).
Typiske skip med en bred skrogform
Typiske skip med en bred skrogform er: tankskip, bulkskip
Disse fartøyene er bygd for å få med seg mest mulig last, og har derfor store lasterom eller lastetanker i skipets skrog. Et stort og fyldig skrog, gir høye koeffisienter.
Skipets fribord har også stor betydning for skipets stabilitet, da skipet vil ha bedre evne til å rette seg opp før dekkshjørnet når vannflaten.
Som dere ser, så er det skipsbyggeren som bestemmer skipets formstabilitet.
Vektstabilitet
Vektstabilitet påvirkes av hvordan alle vektene om bord er plassert. Her har det stor betydning på hvordan lasteoffiseren plasserer lasten. Enkelte skip har også lasteutstyr, som for eksempel store kraner, som påvirker vektstabiliteten til et fartøy. Lovverket setter krav til at stabiliteten til et fartøy skal dokumenteres. Fra lovdata:
Kapittel 2. Stabilitet
**§17 Stabilitetsberegninger
Skip skal ha stabilitetsberegninger, hydrostatikk, KY-kurver, beregninger av brutto- og nettotonnasje og dokumentasjonsunderlag som er utført ved hjelp av et datamaskinsprogram som Sjøfartsdirektoratet har godkjent. Den samme databasen skal benyttes til stabilitets- og tonnasjeberegninger.
Denne type stabilitet kan vi beregne. Alle vekter om bord angis med en avstand fra kjøl til tyngdepunktet til hver enkelt last. Denne er som regel plassert i midten av lastet volum. Det vil si, er et lasterom lastet fullt, så vil det tyngdepunktet være plassert midt i rommet. Er det en container som er lastet jevnt, så er tyngdepunktet til den plassert midt i containeren. Tyngdepunktet til hver enkelt last, angis som VCG (Vertical Center of gravity).
Når vi har samlet alle vektene med deres VCG, så kan vi hjelp av momentregning beregne hvor skipet tyngdepunkt ligger (KG). Det vil si gjennomsnittet av alle vektene.
Skipets tyngdepunkt kaller vi KG, som er avstanden fra kjøl til skipets tyngdepunkt G (gravity).
Med en gang man laster en vekt, losser en vekt eller flytter en vekt, vil tyngdepunktet G flytte seg den retningen som vekten virker. Man kan da beregne GG, altså avstanden G flytter seg, og justere KG opp eller ned alt ettersom hvor vekten flyttes/lastes/losses.
For eksempel et skip har Δ= 300 tonn og en KG= 4,0 m. En vekt på 30 tonn blir flyttet fra dekket med VCG/KG= 5,5 m, ned til et lasterom med VCG/KG= 1,5 m.
Vi kan da beregne hvor mye tyngdepunktet vil flytte seg. Her vil det flytte seg nedover (KG reduseres), fordi vi flytter en vekt som opprinnelig lå høyt oppe i skipet, og ned i lasterommet. Dette vil bedre stabiliteten til fartøyet.
Formelen som skal brukes er: GG1 $= \frac{\text{vekt x arm}}{\Delta}$
Vekten som flyttes er 30 tonn, og armen blir avstanden vekten flyttes. Her vil armen bli mellom VCG’ene. Armen her blir: 5,5 m – 1,5 m= 4 m
Setter tallene inn i formelen: GG1 $= \frac{30\ t\ x\ 4,0\ m}{\Delta300 \ t}$ = 0,4 m
Vi finner da ny KG1 etter flyttingen ved å trekke fra GG1 på den opprinnelige KG.
KG1 = KG - GG1 = 4,0m -0,4m = 3,6 m
Hadde vi flyttet vekten motsatt vei, så ville tyngdepunktet ha hevet seg, og da ville KG blitt tilsvarende større som GG.
Når vi laster eller losser en vekt, så blir tyngdepunktet G også flytte seg. Hvor stor GG blir, avhenger av vektens størrelse i forhold til Δ, og avstanden den har fra KG. Her vil armen i formelen være avstanden mellom opprinnelig KG og vektens VCG.
Ved lasting gjelder denne formelen: GG1 $= \frac{\text{vekt x arm}}{\Delta + \ v}$
Ved lossing gjelder denne formelen: GG1 $= \frac{\text{vekt x arm}}{\Delta - \ v}$
Et skip har et deplasement på 4 000 tonn og en KG på 9,5 meter. Vi tar ombord en last på 100 tonn som plasseres 5 meter under G. Hva blir nytt vertikalt tyngdepunkt?
GG1 $= \frac{\text{vekt x arm}}{\Delta + v}$ = $\frac{100 t \text{ x } 5,0 m}{4000 t + 100 t}$ = 0,122 m
Lastingen av denne vekten, som plasseres under G, vil gjøre at KG blir mindre.
Ny KG1 = KG – GG1 = 9,5m - 0,122m= 9,378 m
Vi ser at ved å laste en vekt under skipets tyngdepunkt, gjør at stabiliteten bedrer seg, KG blir mindre, og da vil GM øke.
Når vi har flere vekter, så er den enkleste og mest oversiktlige metoden for å gjøre dette, å sette opp et momentskjema.
Denne kan vi beregne med å summere alle momentene som alle vektene om bord utgjør. Formelen er som følger: vekt x arm = moment
| Art/plassering | Vekt (tonn) | Arm i meter(KG/VCG) | Vertikalt moment (tonnmeter) |
|---|---|---|---|
| Lettskip | 1060 | 5,70 | 6042 |
| Rom 1 | 400 | 2,81 | 1124 |
| Rom 2 | 400 | 2,70 | 1080 |
| Fuel no 4 | 80 | 0,71 | 56,8 |
| Δ | 1940 | 8302,8 |
$\text{KG} = \frac{\text{Vertikalt moment}}{vekt (\Delta)}$ = $\frac{8302,8\ tm}{1940\ t}$ = 4,28 m
Vi har i eksempelet over funnet ut at skipets tyngdepunkt ligger 4,28 m over kjølen.
Denne kan vi bruke videre til å beregne stabiliteten.
Stabilitetskrav
Myndighetene setter flere ulike krav til stabiliteten er fartøy skal ha. Vi skal ta for oss en og en del, og deretter samle alle til slutt. Det er enkelte skip som for eksempel fiskefartøy som har særkrav.
§ 14. Intakt stabilitet for skip med bruttotonnasje på 50 og derover
Dersom ikke annet er særskilt bestemt, skal følgende minimumskrav tilfredsstilles i enhver lastetilstand, jf. § 15, når krysskurver er beregnet med fri trim:
a) Arealet under kurven for rettende arm (GZ-kurven) skal være minst 0,055 meterradianer regnet opp til en krengevinkel på 30 grader og minst 0,09 meterradianer regnet opp til 40 grader eller fyllingsvinkelen dersom denne er mindre enn 40 grader. I tillegg skal arealet under GZ-kurven mellom krengningsvinklene 30 grader og 40 grader, eller mellom 30 grader og fyllingsvinkelen dersom denne er mindre enn 40 grader, være minst 0,03 meterradianer.
b) Rettende arm (GZ) skal være minst 0,20 m ved en krengevinkel lik eller større enn 30 grader.
c) Krengevinkelen hvor rettende arm har størst verdi, (GZmaks ), bør være større enn 30 grader, og skal aldri være mindre enn 25 grader.
d) Initialmetasenterhøyden (GM) skal være minst 0,15 m.
e) For passasjerskip skal krengevinkelen ikke overskride 10 grader når alle passasjerene plasseres i skipets ene side på ugunstigste måte.
Det første kravet, er at alle skip skal ha en Metansenterhøyde, GM, på minimum 0,15 m. Det er forøvrig særkrav til fiskefartøy, som skal ha en GM på minimum 0,35 m, og fartøy som frakter korn, skal ha GM over 0,30 m.
GM er avstanden fra tyngdepunktet G til metasenteret. Metasenteret er et uttrykk hvor linjen fra oppdriftspunktet treffer senterlinjen. Se figur under.
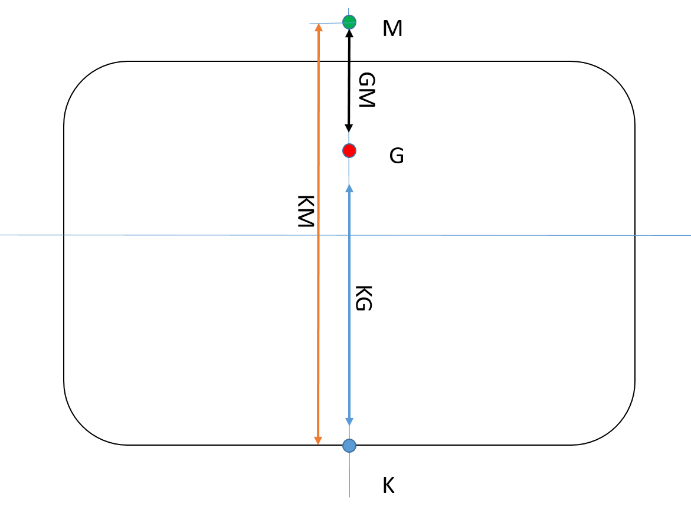
Figur 2.01
Metasenteret sin plassering er beregnet av skipsbyggeren, og man den vil endre seg etter skipets deplasement og dypgang. Man finner KM i skipets hydrostatiske data, og KM er avstanden fra kjøl til metasenteret. Hydrostatiske data er beregninger gjort av skipsbygger eller skipsdesigner, som vil vise de ulike verdiene skipet har ved ulike dypganger og deplasement.
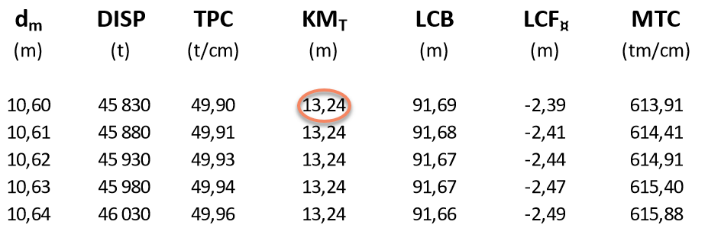
Figur 2.02
| Når et skip har tyngdepunket G, under metasenteret (M), så har skipet en positiv GM, og skipet er stabilt, og vil rette seg opp igjen om en krengning skulle oppstå. |  Figur 2.03. |
| Hvis G og M har samme høyde over kjøl, så er GM = KM, det vil si at GM (metasenterhøyden) er 0. Det vil si at skipet har ingen mulighet til å rette seg opp av seg selv hvis skipet blir utsatt for en krengning. Den vil ligge i samme vinkel, helt til den blir påvirket av en ytre kraft til å legge seg stabilt igjen |  Figur 2.04 |
| Dersom G ligger over M, er GM negativ, og skipet vil mest sannsynlig kantre | 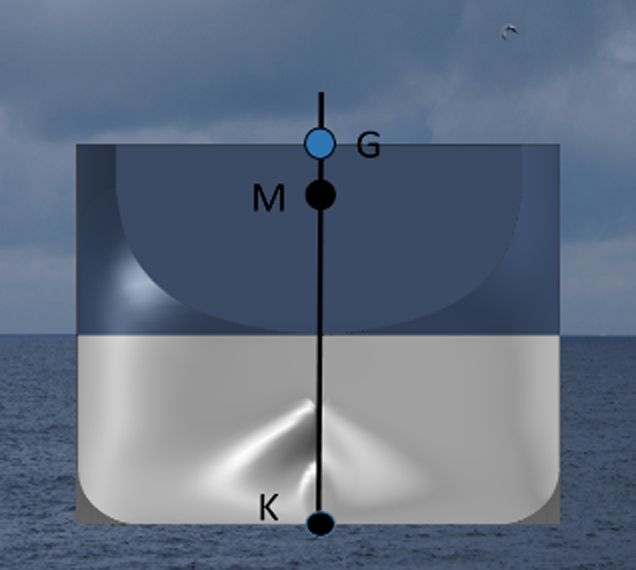 Figur 2.05 |
Etter man har beregnet KG med momentskjema, så tar man ut KM fra hydrostatiske data, og beregner GM. GM= KM – KG. (figur). Det er det første stabilitetskravet man sjekker.
Deretter må man sjekke ut hvor god stabilitet skipet har hvis det blir utsatt for krengning av ulike vinkler.
Initialstabilitet og dynamisk stabilitet.
Vi deler stabilitetsberegningene inn i Initialstabiliet og dynamisk stabilitet.
Initialstabiliet kan også forklares som «begynnelsesstabiliet» opp til krengevinkel 7-10°. Dette gjelder også beregning av GM.
Dynamisk stabilitet er beregninger ved større krengevinkler. Hvor man beregner en krengende arm ved ulike vinkler, og tegner om en GZ-kurve. Arealet under denne beregnes og er dynamisk stabilitet.
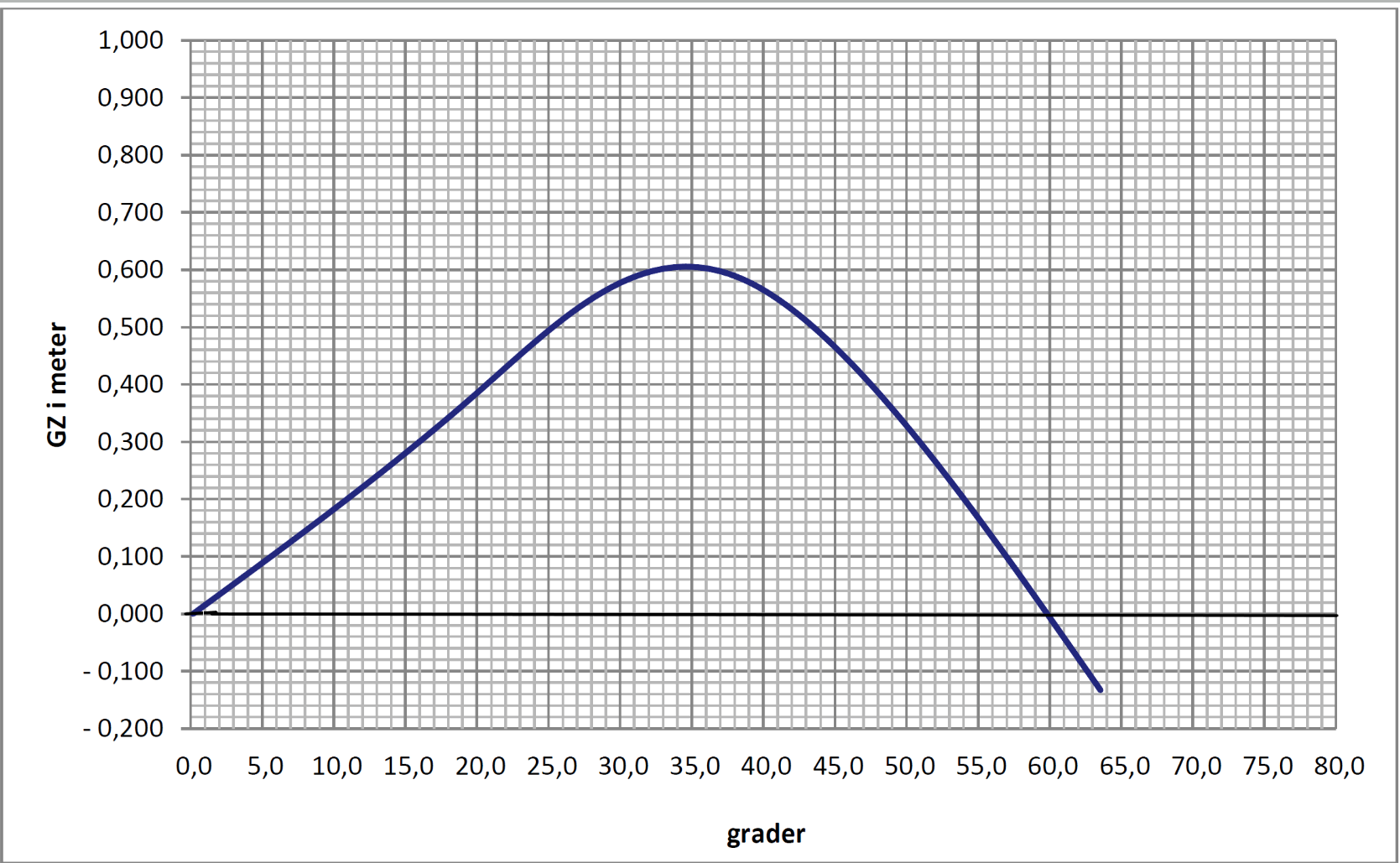
Figur 2.06
Hva skjer når et skip krenger?
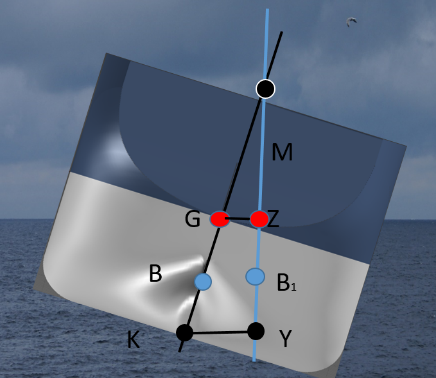
Figur 2.07
Et skip vil krenge av flere ulike årsaker som vær, bølger, vind, ujevn lastfordeling og forskyvning av last for å nevne noen. Når et skip krenger til en side, så vil tyngdepunktet G ikke flytte seg så lenge lasten er sikret godt nok.
Det som skjer er at G står i ro, men oppdriftspunktet B, vil flytte seg til å være i midten av det nye volumet som nå har endret seg over på den ene siden. Det nye oppdriftspunktet kalles B ‘. En linje slåes fra den nye posisjonen til B, og opp til M, og nedover til under kjøl. På denne måten kan vi finne GZ og KY, som beskrives senere i kapittelet.
Når krengevinkelen blir over 10-12°, så vil metasenteret flytte seg. Vi kaller punktet der linjen fra oppdriftspunktet til senterlinjen for det falske metasenteret. Det korrekte metasenteret vil endre seg i takt med skipets krengning til et makspunkt når dekkshjørnet når vannflaten, deretter vil den synke igjen.
Det er derfor det er enkelte formler som kun kan brukes opp til 10-12°, etter det blir formelen unøyaktig. Dette beskrives nærmere i kapittelet med usymmetrisk plassering av vekter og tungløft.
For små krengevinkler opp til 10-12 grader, kan den rettende arm beregnes slik:
GZ = GM x sinФ
Det vil fra oppdriftssenteret og opp til Metasenteret være en oppdriftskraft, og fra Kjøl til tyngdepunktet (G) være en tyngdekraft. Disse to kreftene sammen vil danne et opprettende moment når skipet krenger. Størrelsen på den opprettende armen (GZ) vil bestemme hvor stort momentet blir. Stor GZ vil gi god stabilitet, for da har skipet en tilstrekkelig GM.
En GZ-kurve avhenger av både skipets formstabilitet og vektstabilitet. Økt bredde og høyt fribord vil gi bedre stabilitet, og derfor en GZ kurve som er fyldig og har god utstrekning. Det samme vil et skip som har et lavt tyngdepunkt. Er tyngdepunktet høyt, dvs liten GM, vil kurven bli lavere, mindre fyldig og ikke ha god utstrekning.
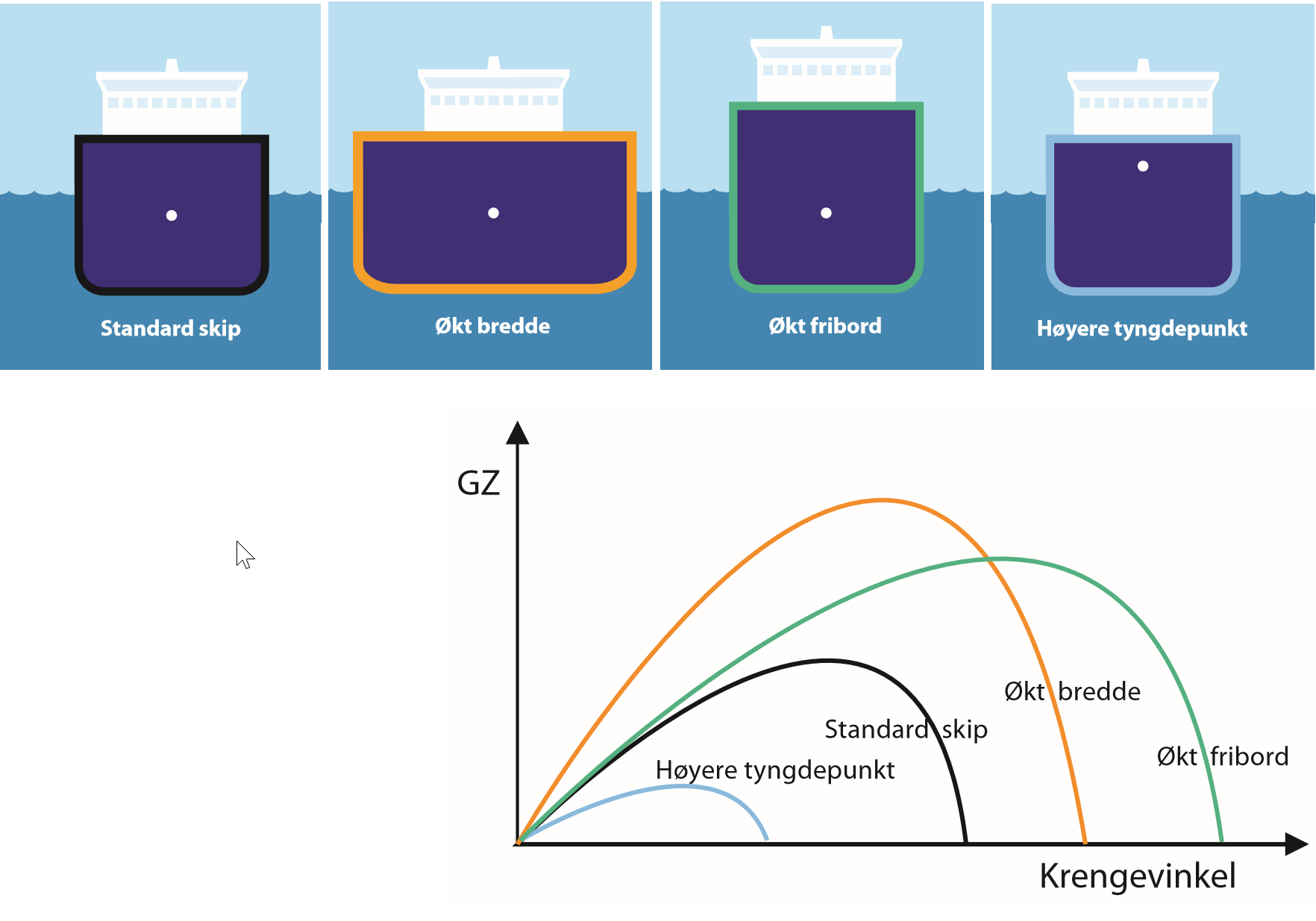
Figur 2.08
Skipsbyggeren kan beregne KY/KN-verdier eller M0S for et skip ved ulike krengevinkler som man bruker for å beregne GZ. Disse taes ut fra skipets hydrostatiske data etter dypgang eller deplasement. Disse verdiene sammen med plasseringen av skipets tyngdepunkt, vil bestemme størrelsen på GZ armen ved de ulike krengevinklene. Man beregner GZ på alle vinklene som er oppgitt i hydrostatiske data, deretter tegner man kurven.
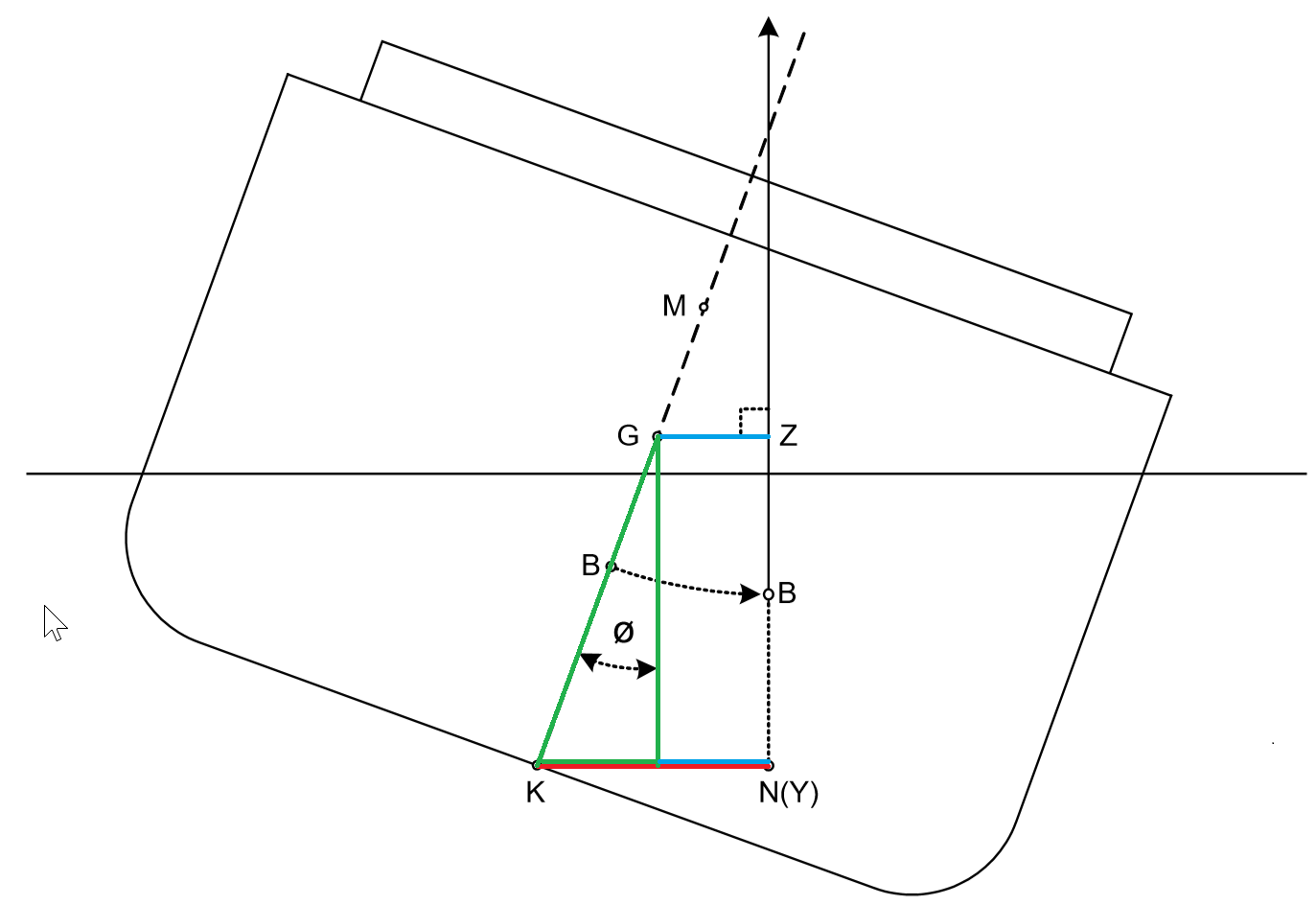
Figur 2.09
GZ = KY/KN – KG x sinФ (Linda og Sidus)
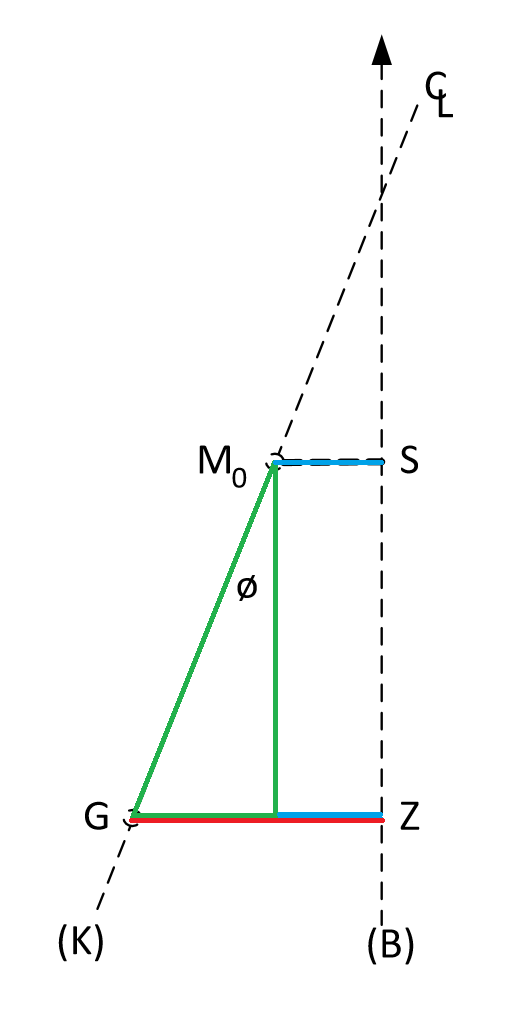
Figur 2.10
GZ = M0S + GM x sinФ (Mercandien Importer)
Angle of loll
Hvis et skip har negativ GM, vil ikke skipet ha et opprettende moment på små vinkler, og den rettende armen, GZ, vil være negativ. Angle og loll er de gradene på GZ kurven som er negativ som vi ser på figuren under er fra 0ᵒtil cirka 10ᵒ. Hvis en ytre påvirkning gjør at skipet krenger til en vinkel hvor skipet ikke har et rettende moment, så vil ikke skipet rette seg opp av seg selv før krengningen blir like stor som når GZ er positiv igjen. På figuren vil det være ved 10ᵒ. Vi ser at skip som har negativ begynnelsesstabilitet og negativ GZ likevel kan ha positiv stabilitet ved større krengninger.
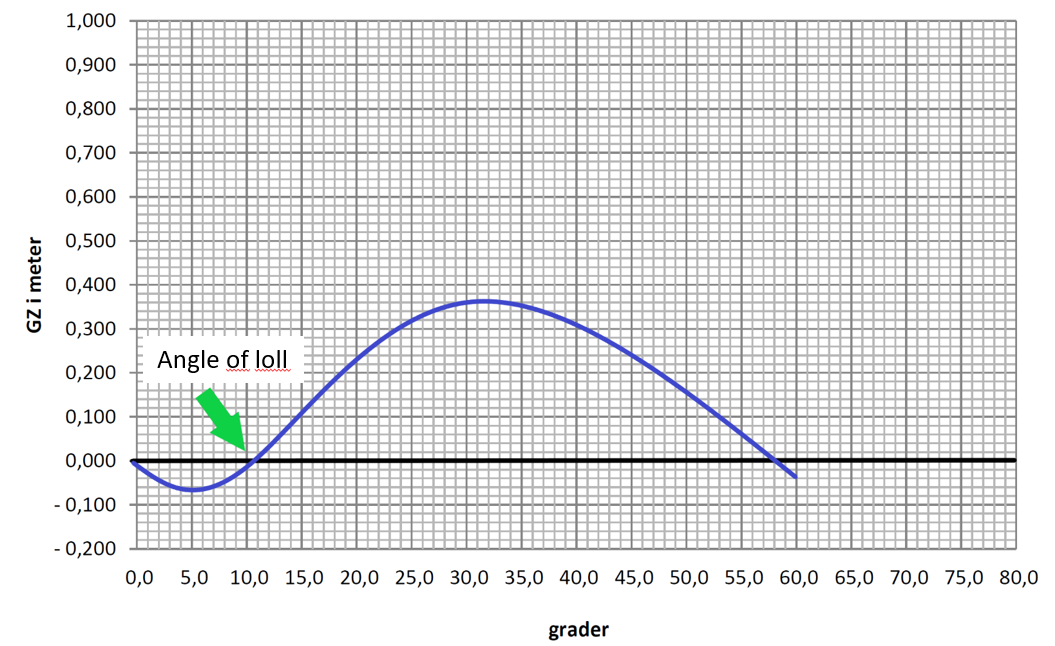
Figur 2.11
Beregningseksempel GZ
Beregningseksempel:
M/S Mercandian Importer har etter lasting et deplasement på 3913 tonn. Sum moment vertikalt er 18 501 tm.
a) Hva blir skipets korrigerte KG og GM etter lasting?
b) Tegn GZ-kurven.
c) Regn ut dynamisk stabilitet kontroller mot regelkrav .
a)
Skipet deplasement etter lasting 3 913,00 tonn
Sum skipet vertikale moment 18 748,00 tm
KG2 = $\frac{\text{Vertikalt moment}}{\text{Deplasement}}$ = $\frac{18748\ tm}{3913\ t}$ =
KG2 = 4,791 m
| KM | 5,480 | meter |
| KG2 | 4,791 | meter |
| G2M | 0,689 | meter |
b)
Bruker formelen GZ = M0S + (GM * sinØ)
| Krengningsvinkel i grader | M0S | GM * (sin Ø) | GZ i meter |
|---|---|---|---|
| 0 | 0,000 | ||
| 10 | 0,003 | 0,120 | 0,123 |
| 20 | -0,005 | 0,236 | 0,231 |
| 30 | -0,095 | 0,344 | 0,249 |
| 45 | -0,233 | 0,487 | 0,254 |
| 60 | -0,520 | 0,597 | 0,077 |
| 75 | -0,875 | 0,665 | -0,210 |
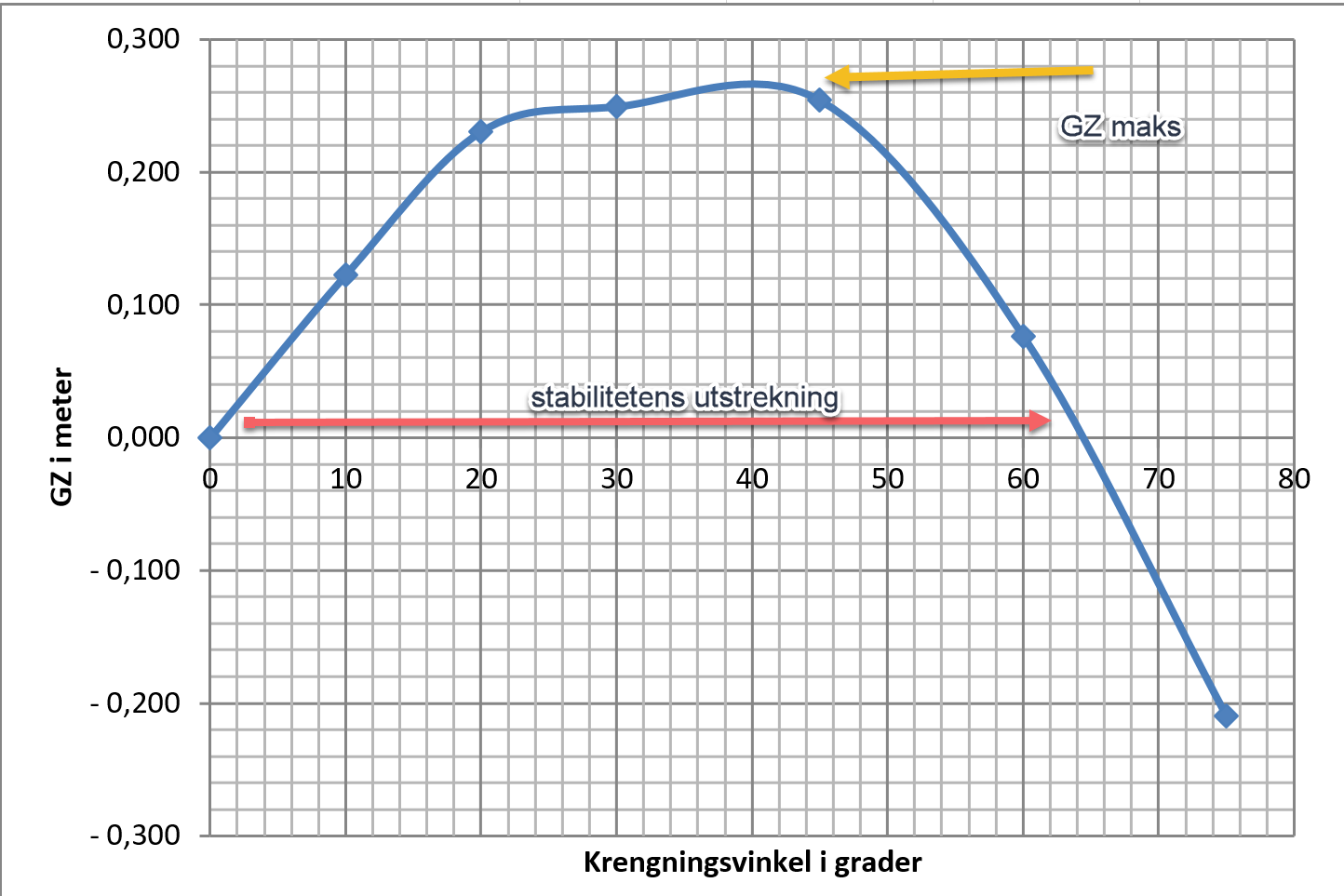
Figur 2.12
Når man har en beregnet og tegnet GZ-kurve, så kan man sjekke om kurven tilfredsstiller kravene til stabilitet, gitt av SOLAS. Deretter beregner man arealet av kurven ved hjelp av Simpsons formel. Det stilles minimumskrav til dette arealet i mrad, så man beregne gradene over i radianer. Vi kjenner til Simpsons formel slik:
Areal= $\frac{\text{høyde x Produkt}}{3}$
Høyden vil her være 5° fordi vi tar ut GZ-verdien for hver femte grad, og siden produktet vårt er i meter, vil svaret her komme i metergrader. Vi må derfor beregne det over i radianer slik:
Areal= $\frac{\text{høyde x Produkt}}{3}$ x $\frac{\pi}{180}$
Beregningseksempel fortsettelse
Når man skal beregne dynamisk stabilitet, så må vi bruke GZ-kurven vi har beregnet og tegnet til å lese av GZ-verdiene for hver femte grad. Siden et stabilitetskrav er fra 0-30°, et fra 30-40° og et fra 0-40°, så må vi dele opp beregningene i tre.
Avlesningen av GZ starter på 0, og vi leser av de gradene som vi ikke har beregnet tidligere i oppgaven.

Figur 2.13
| Ordinat nummer | Ord. lengde | Simpsons faktor | Produkt |
|---|---|---|---|
| 1 | 0,00 | 1 | 0,00 |
| 2 | 0,06 | 4 | 0,24 |
| 3 | 0,12 | 2 | 0,25 |
| 4 | 0,18 | 4 | 0,72 |
| 5 | 0,23 | 2 | 0,46 |
| 6 | 0,25 | 4 | 1,00 |
| 7 | 0,25 | 1 | 0,25 |
| $\Sigma$ produkt 0–30 | 2,92 |
| Ordinat nummer | Ord. lengde | Simpsons faktor | Produkt |
|---|---|---|---|
| 7 | 0,25 | 1 | 0,25 |
| 8 | 0,26 | 4 | 1,04 |
| 9 | 0,27 | 1 | 0,27 |
| $\Sigma$ produkt 30–40 | 1,56 |
Areal 0-30° = $\frac{\text{h x } \Sigma\text{ Produkt 0–30 }}{3}$ x $\frac{\pi}{180}$ = $\frac{5 \text{° x 2,92 m}}{3}$ x $\frac{\pi}{180}$ = 0,085 m rad
Areal 30-40°= $\frac{\text{h x } \Sigma\text{ Produkt 30–40 }}{3}$ x $\frac{\pi}{180}$ = $\frac{5 \text{° x 1,56m}}{3}$ x $\frac{\pi}{180}$ = 0,045 m rad
Areal 0-40° = 0,085 m rad + 0,045 m rad = 0,13 m rad
| Stabilitetskrav: | Krav til areal under kurven: |
|---|---|
| GM $\leq$ 0,15m | 0-30° = 0,055 mrad |
| GZ v/30°$\leq$ 0,20 m | 30°-40° = 0,03 mrad |
| GZ maks skal være etter 25-30° | 0-40° = 0,09 mrad |
Fri væskeoverflate effekten.
Noe som kan redusere stabiliteten betraktelig er effekten av fri væskeoverflate. Når en tank ikke er full eller tom, så vil væsken i tanken bevege seg fra side til side når skipet beveger seg. Dette gjelder spesielt tanker som man har forbruk fra under reisen, som f.eks bunkerstanker, ferskvannstanker osv. Selv om de er fulle da sjøreisen starter, vil de etter en stund være slik at væsken kan skvalpe fra side til side i tanken. Vi sier da at tanken har fri væskeoverflate.
Samme skjer også i ballasttanker og lastetanker hvis de ikke er helt fulle.
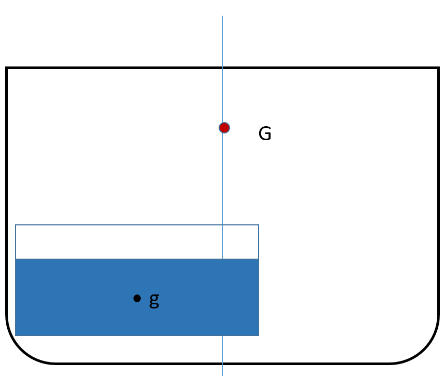
Figur 2.14
Figuren over viser tverrsnittet av et skip med en halvfull/slakk tank. Tyngdepunktet til skipet er merket med G, mens tyngdepunktet i væsken i tanken er merket med g.
Når skipet krenger, forskyver noe av væsken i tanken seg. Det ser du på figuren under. Figuren viser at et volum med et trekantet tverrsnitt forskyver seg til den siden som skipet krenger. Det fører til at tyngdepunktet til skipet forskyver seg fra G til G2.
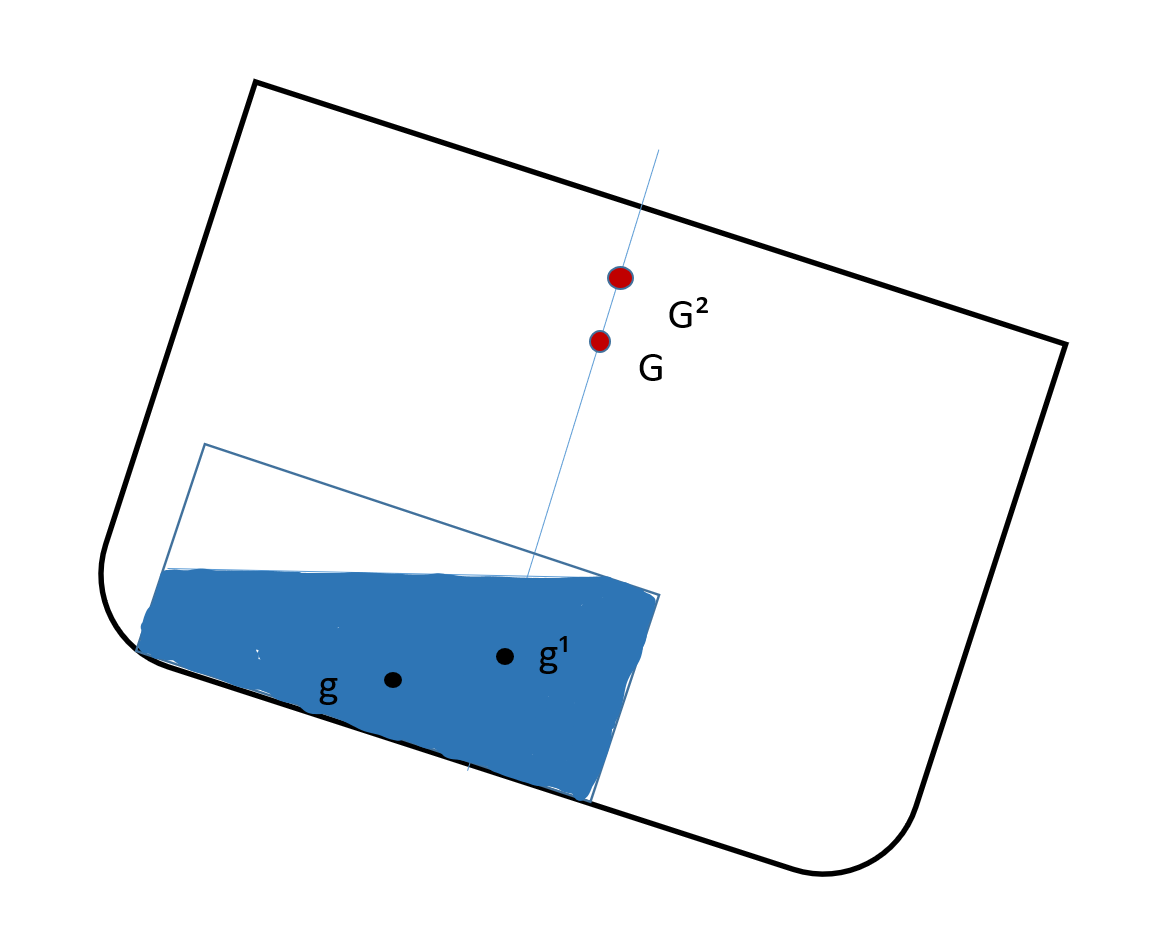
Figur 2.15
Tyngdepunktet til væsken i tanken forskyver seg fra g til g¹. Denne forskyvningen er egentlig med på å øke det krengende momentet, men fordi forskyvningen kommer av noe i selve skipet og ikke av en kraft utenfra, ser vi det som en reduksjon av stabiliteten til skipet.
Vi regner denne reduksjonen som en heving av tyngdepunktet til skipet.
Denne hevingen av tyngdepunktet (G) beregner vi slik:
$GG_2=\frac{densitet(\frac{t}{m^3}) \text{ x I} (\text{tregjetsmomentet }m\text{4})}{\Delta t}$ = $\frac{\text{fri væskeoverflate moment} (tm)}{\Delta t}$
Deretter korrigerer vi KG for GG2 grunnet den frie væskeoverflaten, ved å legge de sammen.Det er fordi stabiliteten blir dårligere, da går G oppover som gir en mindre GM.
Nesten fulle eller nesten tomme tanker gir mindre reduksjon enn halvfulle tanker. Av og til regner man med «worst case scenario», og tar beregner med den verste kondisjonen, det vil si halvfull tank. Det er ikke bare halvfulle tanker som gir fri væskeoverflate effekt, men også vann på dekk som følge av vanninntrenging eller brannslokking. Hvor stort fri væskeoverflatemoment en slakk tank har, kommer an på tankens treghetsmoment. Enkelt forklart vil en tank som gir vannets overflate stort areal, har høyt treghetsmoment.
Hvis en tank er firkantet, kan treghetsmomentet beregnes slik, hvor I= treghetsmoment.
I = $\frac{l\ \text{ x } b^3}{12}$
Vi har sett fatale ulykker på grunn av fri væskeoverflate, f. eks «Estonia» og «Herald of Free Enterprise», som begge fikk vanninntrenging på bildekk på grunn av baugporten ikke fungerte.

Vi kan regne forflytning av G ved ulike situasjoner, etter hvilke opplysninger vi har tilgjengelige.
1. Hvis vi kjenner til lengde, bredde, vektdeplasement og densitet på væsken i tanken.
GG2 = $\frac{\text{l x } b^{3} \text{ x densitet}}{12\ x\ \Delta}$
2. Hvis vi kjenner treghetsmomentet, I (m4), i en tank (f.eks ballasttankene på Linda)
$GG_2 = \frac{\text{I x densitet}}{\Delta}$
Dette er samme formel som den ovenfor, fordi I $= \frac{\text{l x}b^{3}}{12}$
3. Hvis vi kjenner fri væskeoverflate momentet (tm), som er I x densitet, så kan vi sette:
$GG_2 = \frac{FSM\ (tm)}{\Delta}$
Bruk av lasteromstabeller for å finne korrekt VCG i et lasterom og korrekt VCG og FSM i en tank.
VCG (Vertically center of gravity) viser avstanden fra kjølen og til tyngdepunktet til en enkeltlast. Dette tyngdepunktet vil i de fleste tilfeller være midt i volumet av lasten.
Når man skal ha last i lasterommene, så må man beregne rett volum av lasten, og deretter finne rett VCG for akkurat den kondisjonen. Man må også vite om man skal bruke tabellene for «grain» eller «bales». «Grain» betyr korn, men brukes ved alle løse bulklaster fordi lasten vil fylle rommet rundt kneplater etc. «Bales» brukes ved stykkgods, for eksempel last på paller. Her vil man gjerne ha mindre volum tilgjengelig siden denne lasten ikke kan fylles i hele rommet pga konstruksjonen.
Et eksempel:
I rom 1 på Sidus er det lastet kun 1985 m³. For å finne rett VCG til den aktuelle lastemengden, så må man gå inn i ressursheftet i «grain loading plan» og bruke kubikken som er lastet i rommet.
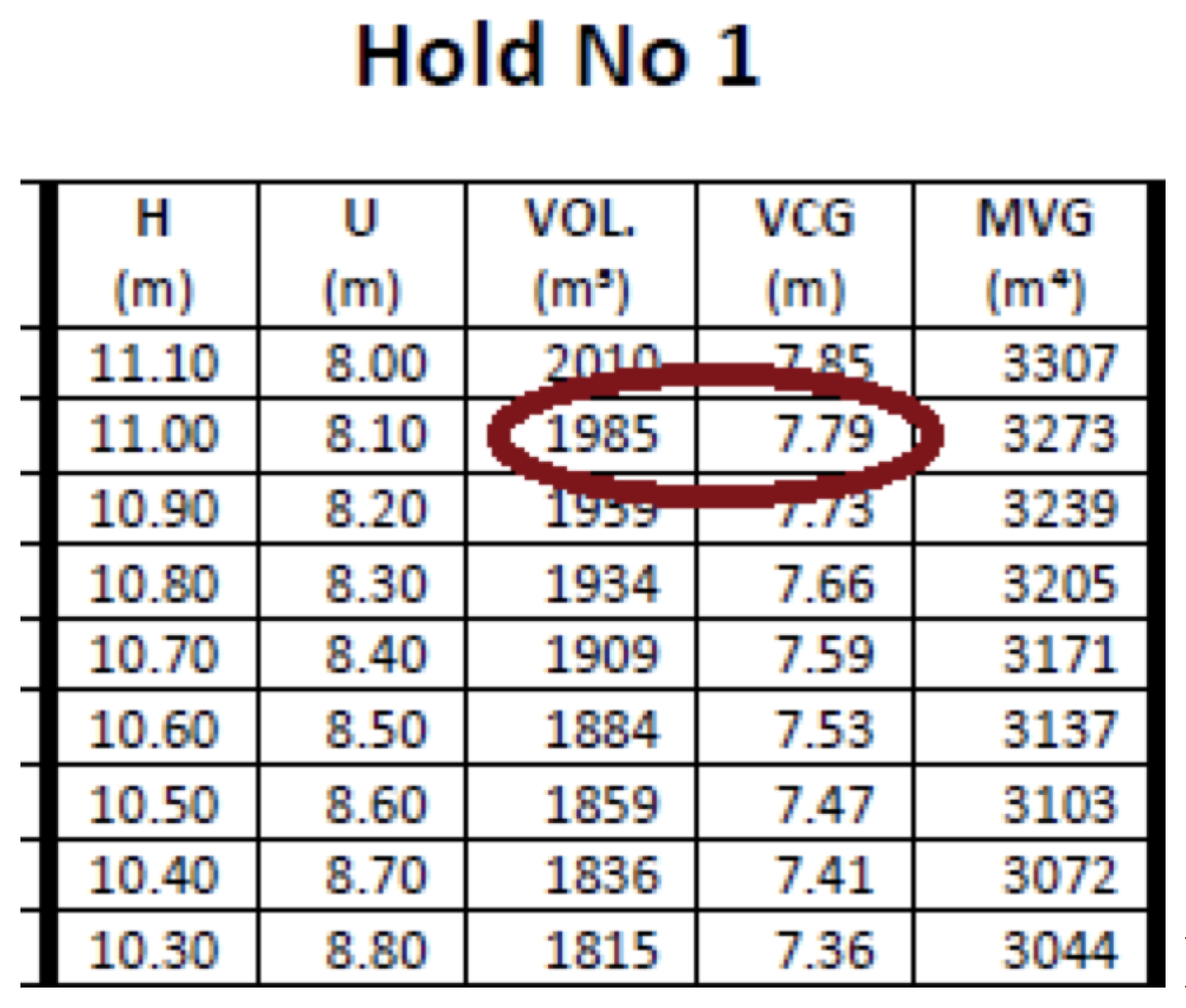
Figur 2.17
Her vil korrekt VCG være 7,79 m.
Samme metode bruker man på å finne rett VCG og FSM i ballasttanker, tungoljetanker etc.
For å beregne volum ut fra vekt i hvert rom, så trenger vi å vite stuasjefaktoren.
Vi vet hvor store lasterom vi har på skipene, altså hvor mange kubikk (m³) vi har tilgjengelig. Men vekten av det vi laster, avhenger jo av hvilken last som lastes, og dens egenvekt.
Det er stor forskjell på skipets vekt om vi laster fullt i alle rom med en lett last, eller om vi laster en tung last. Derfor er egenvekten viktig å vite.
Når man laster løs bulklast eller stykkgods, får man gjerne oppgitt stuingsfaktor/stuasjefaktor (SF), som sier hvor mange kubikk ett tonn tar av plass. Denne varierer fra produkt til produkt.
Et eksempel: Vi har et lasterom på 3000 m³ som skal lastes med en last som har en stuingsfaktor på 1,5 m³/tonn. For å finne vekten av lasten vi får plass til må vi gjøre slik:
$vekt = \frac{volum\ (m3)}{\text{stuingsfaktor}} = \frac{3000\ \cancel{\color{#8a0f00}{m3}}}{1,5 \cancel{\color{#8a0f00}{m^3}}/tonn}$ = 2000 tonn.
Det vil si, at hvis vi laster 3000 m³ med en stuingsfaktor på 1,5 m³/ton, så vil lasten veie 2000 tonn.
Hvis vi vet hvor mye lasten veier, f.eks 2000 tonn. Så må vi regne den om til kubikk hvis vi skal ta ut rett VCG, som vil avhenge av hvor full lasterommet er.
Da må vi snu formelen:
Volum = Vekt x stuingsfaktoren= 2000 tonn x 1,5 m³/tonn = 3000 m³
Når man laster flytende laster eller bunkers, ferskvann o.l. bruker man densitet, som er oppgitt i tonn/m3.
Eksempel
Eksempel: (bruker samme tall som over)
En tank har kubikk på 3000m³, og laster en last med densitet 1,5 t/m³.
Da blir vekten = volum (m³) x densitet (t/m³)= 3000 m³ x 1,5 t/m³ = 4500 tonn
Kan snu denne formelen for å finne antall kubikk hvis vi vet antall tonn:
$volum = \frac{vekt\ (tonn)}{densitet (\frac{t}{m^3})}$
Det er viktig å sette opp med benevning, for da ser dere om svaret kommer ut med rett benevnelse.

