1. Teori grunnlag
Hva skal vi lære
Vi beskriver kort grunnleggende teori med tilknytning til drift og vedlikehold av skipsmaskineri.
1.1 Termodynamikk
Innledning - energiloven
Energiloven, også kalt 1. hovedsetning, er en erfarings-lov som kan formuleres slik:
Energi kan verken oppstå eller forsvinne, den kan bare omformes fra en form til en annen.
Av dette følger at den totale energien i et system er konstant. Den energien vi «ser» rundt oss i forskjellige former har derfor alltid eksistert. Når vi forbruker energi, for eksempel til fremdrift av et skip, vil energien ikke forsvinne, men den vil gå over til en lavere kvalitet, slik at vi ikke kan utnytte den til nyttig arbeid. Ved bruk av energiloven skiller vi mellom et lukket- og åpent system.
1.1.1 Energiomforming – Lukket system (sylinderprosess)
Lukket system (sylinderprosess)
Et lukket system er kjennetegnet ved at stoffmengden i systemet er konstant, mens energi i form av varme eller arbeid kan passere systemgrensen.

Figuren viser et lukket system der systemgrensen omslutter gassen i en sylinder med et bevegelig stempel.
Systemgrensen kan her flyttes, men massen er konstant og vi har derfor et lukket system.
Energi i form av varme (Q) eller arbeid (W) kan bli ført inn eller ut av systemet.
For dette systemet får vi energiligningen: Q = ΔU + W (ΔU = endring av indre energi)
Varme og arbeid
Varme er definert som energioverføring forårsaket av en temperaturforskjell. Overført varme ved henholdsvis konstant trykk og konstant volum er bestemt ved:
Konstant trykk: Qp = m(kg) ⋅ cp(kJ/kgK) ⋅ (T2 − T1)(K) (kJ)
Konstant volum: Qv = m(kg) ⋅ cv(kJ/kgK) ⋅ (T2 − T1)(K) (kJ)
Her er cp og cv spesifikk varmekapasitet[^1] ved henholdsvis konstant trykk og konstant volum.
Når både trykk og volum endres, er overført varmemengde avhengig av hvordan denne overføringen foregår, og vi må da ha flere opplysninger om prosessen for å beregne overført varmemengde. Dette kommer vi tilbake til senere.
Arbeid (W)
Mekanisk arbeid (W) er produktet av kraft og forskyvning langs kraftens angrepslinje. I en sylinder med et bevegelig stempel blir kraften F = p⋅A, der p er trykk i N/m2 og A er areal i m2.
I regelen er trykket i en sylinder ikke konstant under arbeidsslaget, men varierer i forhold til stempelets posisjon. For å ta hensyn til dette, må vi i prinsippet bruke integralregning og får da at utført arbeidet (W) er lik arealet under tilstandskurven i et pV diagram. Se figuren under.
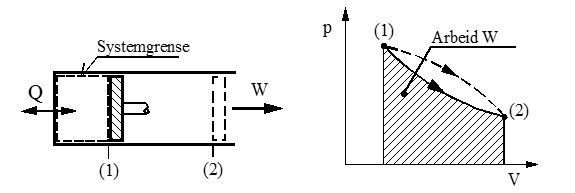
I figuren under er vist et lukket system, der en gass ekspanderer fra tilstand (1) til (2) langs den heltrukne ekspansjonskurven. Gassen utfører da arbeidet W = skravert areal. Merk at den stiplete ekspansjonskurven gir forskjellig areal, dvs. W er en funksjon av «veien» mellom de to tilstandene.
Når tilstandskurven er kjent, kan vi derfor beregne gass-arbeidet ved innsetting i diverse formler, se formelsamlingen.
Polytrop tilstandsendring i motorsylindre
En polytrop tilstandsendring er definert ved:
Polytrop tilstandsendring
p ⋅ ${V^n}$ = konstant ⇒ p1 ⋅ $\mathrm{V}_1^\mathrm{n}$ = p2 ⋅ $\mathrm{V}_2^\mathrm{n}$
p ⋅ ${V^n}$ = konstant ⇒ p1 ⋅ $\mathrm{V}_1^\mathrm{n}$ = p2 ⋅ $\mathrm{V}_2^\mathrm{n}$
n = polytropeksponent (n ≈ 1,3 - 1,36 for kompresjon)
Kompresjon av luft og ekspansjon av forbrenningsgasser i en motorsylinder er eksempel på polytrope prosesser. Indre friksjonstap i slike motorprosesser er som regel, små sammenlignet med arbeid utviklet i sylinderen (indikert arbeid), og vi kan derfor se bort fra indre tap. Overført arbeid (W) blir da lik volumendringsarbeidet. (Se formelsamling).
W = $\mathop \smallint \limits_1^2 $pdV = $\frac{{\mathop p\nolimits_1 \mathop V\nolimits_1 - \mathop p\nolimits_2 \mathop V\nolimits_2 }}{{n - 1}}$= $\frac{{mR({T_1} - {T_2})}}{{n - 1}}$ (J)
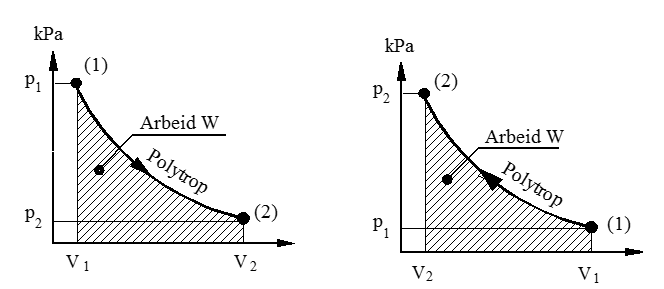
Polytrop ekspansjon Polytrop kompresjon
For polytrop kompresjon får vi kompresjonstrykket (pk):
pk = p1 ⋅ ${\left( {\frac{{{V_1}}}{{{V_2}}}} \right)^n}$ (kPa)
Her er (pk) kompresjonstrykket i kPa, (p1) er starttrykket i kPa, (V1) er startvolumet i m3, (V2) er sluttvolumet i m3 og (n) er polytropeksponenten. (Alle trykk i absolutt verdi).
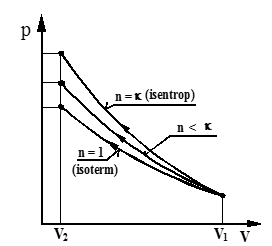
I figuren over er vist tre eksempler på polytrop kompresjon i et pV-diagram.
Merk at lav n–verdi gir lavt kompresjonstrykk.
Lavt kompresjonstrykk kan i prinsippet skyldes sterk kjøling, men i praksis er lavt kompresjonstrykk som regel, et tegn på feil ved kompresjonsringene eller lekke avgass- og/eller innsugsventiler.
Polytrop kompresjon
Ved energianalyse av motorprosesser kan vi som nevnt, se bort fra indre tap. Om vi også ser bort fra lekkasjer, får vi følgende sammenheng mellom varmeoverføring og n-verdier for henholdsvis polytrop kompresjon og ekspansjon i en motorsylinder:
Polytrop kompresjon i sylindere
-
Under første del av kompresjonen er sylinderveggene varmere enn luften, og varme blir da overført fra sylinder til gass, dvs. varme blir tilført prosessen, og vi får n > κ.
-
Etter hvert stiger lufttemperaturen på grunn av kompresjonen, og varme blir da overført fra gass til sylindervegger og videre til kjølevann, dvs. n < κ.
-
For kompresjonen under ett får vi vanligvis n-verdier omkring 1,33 til 1,36. Dette indikerer at det totalt sett blir bortført varme fra gassen til sylinderveggen og videre til kjølevannet.
Polytrop ekspansjon i sylindere
-
Under første del av ekspansjonsslaget foregår det vanligvis en viss etterbrann. Det betyr at varme blir tilført gassen i sylinderen. Polytropeksponenten (n) er derfor normalt lav under første del av ekspansjonsslaget, varierer typisk fra n = 1 til 1,15.
-
Under den videre ekspansjonen vil forbrenningen gradvis avta og til slutt å dø ut, og varmetilførselen vil derfor gradvis avta. Polytropeksponenten vil derfor gradvis øke.
-
For hele ekspansjonsslaget varierer n typisk mellom n = 1,3 og n = 1.35. Dette indikerer at det totalt sett blir tilført varme under ekspansjonsslaget, dvs. det foregår normalt en viss etter-brann under ekspansjonsslaget.
Et åpent system, også kalt kontrollvolum, er kjennetegnet ved at stoffmengder og energi kan passere systemgrensen. Ved studie av slike system skiller vi mellom strømningsprosesser der det ikke utveksles arbeid og arbeidsprosesser der hensikten er utveksling av arbeid.
For å beregne overført arbeid i strømningsmaskiner innfører vi begrepene entalpi (h) og teknisk arbeid (wt). Før vi fortsetter, skal vi derfor definere disse begrepene.
Entalpi (h) - definisjon
Ved strømningsberegninger forekommer ledd som (u + pv) ofte. Denne størrelsen er derfor gitt et eget navn, entalpi med symbol (h), definert slik:
h = u + pv (kJ/kg)
Der u er spesifikk indre energi i kJ/kg og pv er såkalt ytre energi i kJ/kg, p er trykk i kPa abs. og v er spesifikt volum i m3/kg.
For entalpi gjelder at kun endringer har praktisk interesse og vi kan derfor velge referanseverdier etter behov. For vann velger vi for eksempel h = 0 ved 0°C, entalpien for damp ved 0°C blir derfor omkring 2500 kJ/kg, som tilsvarer vannets fordampningsvarme ved 0°C. For kuldemedier setter vi h = 200 kJ/kg ved 0°C, dette for å unngå negative skala-verdier i diagram og tabeller for kuldemedier.
For ideell gass og konstant cp gjelder:
h2 − h1 = cp ⋅ (T2 − T1) (kJ/kg)
h2 − h1 = endring av spesifikk entalpi (kJ/kg)
cp = spesifikk varmekapasitet ved konstant trykk (kJ/kgK)
Herav følger at endring av entalpi er like stor som tilført, eller bortført varmemengde ved konstant trykk. Merk likevel at entalpi er sammensatt av tilstandsstørrelsene u, p og v, og er derfor også en tilstandsstørrelse, mens varme er en energioverføring.
Stagnasjonstilstand
I en del tekniske prosesser blir gasshastigheten plutselig endret. Dette skjer for eksempel i en turboladet dieselmotor. Eksosgassen strømmer der ut fra sylindrene med stor hastighet og inn i en beholder, kalt receiver, der gasshastigheten blir bremset opp, nesten til null. Gassens kinetiske energi blir da omformet og lagret i form av økt indre energi i receiveren, noe som er hovedårsaken til at gasstemperaturen er omkring 40-50°C høyere i receiver enn i utløpet fra sylindrene. (Merk at tilsvarende oppbremsing og temperaturøkning også skjer ved støtdrift).
Eksempel
Eksempel - stagnasjonstemperatur
Luft med temperatur 42°C strømmer i en rørledning. En ventil i rørledningen blir så brått stengt og luftstrømmen stanser opp. En slik oppbremsing innebærer i prinsippet at luftens energiinnhold blir endret fra entalpi til indre energi, dvs. h1 = u2, som gir følgende:
cp ⋅ T1 = cv ⋅ T2 ⇒ T2 = T1 ⋅ $\frac{{{c_p}}}{{{c_v}}}$ = 315 ⋅ $\frac{\mathrm{1,005\ kJ/kg}}{\mathrm{0,715\ kJ/kg}}$ = 441 K = 168°C
Temperaturen øker altså fra 42°C til 168°C.
Teknisk arbeid (Wt)
Vi ser på arbeidsprosesser i åpne system (strømningsmaskiner).
I figuren under er vist eksempel på et åpent system, der det foregår en kontinuerlig massestrøm gass/damp gjennom en turbin. Ved analyse av slike åpne system ser vi på stofftilstanden ved innløp (1) og utløp (2) av det valgte systemet.
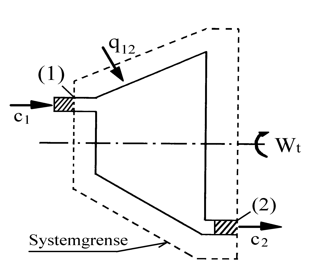
For systemet vist i figuren får vi energiligningen:
q = h2 − h1 + Wt + $\frac{1}{2}$(c22 − c12) ⋅ 10−3
q = varmeoverføring (kJ/kg)
h1 = entalpi inn (kJ/kg)
h2 = entalpi ut (kJ/kg)
Wt = teknisk arbeid (kJ/kg)
c1 = hastighet inn (m/s)
c2 = hastighet ut (m/s)
Ved mange tekniske beregninger er forskjell i hastighet inn og ut av strømningsmaskiner liten og vi kan derfor sløyfe hastighetsleddet i ligningen. Videre er massestrømmen oftest så stor at det ikke er tid til noen varmeoverføring av betydning og vi kan derfor også sette overført varme q = 0.
For de fleste strømningsmaskiner (dampturbiner, turboladere og gassturbiner mv.) får vi da følgende uttrykk for teknisk arbeid (wt):
wt = h1 − h2 (kJ/kg) (1)
Spesifikt teknisk arbeid (akselarbeidet) er altså lik arbeidsmediets spesifikke entalpiendring.
Ved å multiplisere med massestrømmen får vi akseleffekten (P):
P(kW) = m ⋅ (kg/s) ⋅ wt (kJ/kg) = m ⋅ (kg/s) ⋅ (h1 − h2)(kJ/kg) (2)
For gasser beregner vi entalpiendringer slik; (h1 − h2) = cp ⋅ (T1 − T2), mens vi for damp må avlese entalpien i mollier-diagram eller damptabeller, dette fordi damp ikke følger gasslovene.
*Merk at det er ingen forskjell mellom de to typer arbeid. Både mekanisk arbeid (W) og teknisk arbeid (wt) er definert på samme måte; Arbeid = kraft×vei. Forskjellen er i korthet at mekanisk arbeid er utledet for en lukket prosess, mens teknisk arbeid er utledet for en åpen prosess. Dette betyr at formlene vi bruker er forskjellige, mens arbeidet vi får ut er likeverdig. *
Merk
Merk også at formler for teknisk arbeid i formelsamlingen gjelder kun for tapsfrie prosesser og er derfor ikke gyldige for virkelige maskiner.
Ved beregning av teknisk arbeid bruker vi derfor formel (1) eller (2), som vist over.
1.1.3 Energikvalitet og entropi
De ulike energiformer kan i stor grad omformes. I en forbrenningsmotor skjer denne omformingen ved at kjemisk bundet energi blir frigjort ved forbrenning og omformet til varme. Varmen gir økning av trykkenergien, og via stempel og veivstang blir denne trykkenergien omformet til mekanisk arbeid på veivakselen. Dette arbeidet får vi ut i form av et dreiemoment, som for eksempel kan dreie hjulene på en bil. Dermed går det mekaniske arbeidet over til kinetisk energi.
Dersom motoren driver en vannpumpe, vil pumpa omforme det mekaniske arbeidet til trykkenergi (økt vanntrykk), stillingsenergi (pumpe til et høyere nivå) eller økt bevegelsesenergi (vannets hastighet øker).
Elektrisk energi og varme er de energiformer som er mest brukt i praksis. Av disse kan elektrisk energi stort sett ubegrenset omformes til såvel varme som til de fleste andre energiformer.
At vi ikke får omdannet all den elektriske energien til for eksempel mekanisk energi, skyldes en «ufullkommen» maskin, det finnes altså ingen naturlov som forbyr dette.
Ved studie av varmekraftmaskiner er det viktig å være klar over at det ifølge 2. hovedsetning bare er mulig å omforme varme til arbeid dersom vi samtidig bortfører en del av varmen.
Generelt gjelder altså at noen energiformer er ubegrenset mulig å omforme (høyverdige), mens andre bare er begrenset mulig eller umulig å omforme til andre energiformer[^2]. De viktigste energiformer i denne sammenheng er:
| *Energi som kan om formes ubegrenset * (Høyverdig) | Energi som i begrenset grad kan omformes (Kvalitet - temperaturavhengig) | Energi som ikke direkte kan omformes som er i likevekt med omgivelsene * (Lavverdig) |
|---|---|---|
|
|
|
Merk at lavverdig energi også kan omformes, f.eks. i varmepumper e.l., men dette krever altså samtidig bruk av energi i form av arbeid.
Bruken av 2. hovedsetning, også kalt entropiloven, blir ofte knyttet til begrepet entropi. Før vi går videre skal vi derfor introdusere begrepet entropi. Se neste side.
Entropi (s)
Entropi
Entropi[^3] er en «konstruert» størrelse, opprinnelig utledet som en følge av 2. hovedsetning.
Entropi er med andre ord et teoretisk eller abstrakt begrep, som vi derfor ikke kan forklare (mange har uten hell, gjort forsøk på dette opp gjennom årene).
For gasser får vi ved utledning, følgende formler for entropiendring (Δs), (se formelsamling):
Formel for entropiendring
Δs =${\rm{ }}{{\rm{c}}_{\rm{v}}} \cdot {\rm{ln}}\frac{{\mathop {\rm{T}}\nolimits_{\rm{2}} }}{{\mathop {\rm{T}}\nolimits_{\rm{1}} }}{\rm{ + R}} \cdot {\rm{ln}}\frac{{\mathop {\rm{v}}\nolimits_{\rm{2}} }}{{\mathop {\rm{v}}\nolimits_{\rm{1}} }}$ (kJ/kgK)
Eller:
Δs =${\rm{ }}{{\rm{c}}_{\rm{p}}} \cdot {\rm{ln}}\frac{{\mathop {\rm{T}}\nolimits_{\rm{2}} }}{{\mathop {\rm{T}}\nolimits_{\rm{1}} }}{\rm{ }} - {\rm{ R}} \cdot {\rm{ln}}\frac{{\mathop {\rm{p}}\nolimits_{\rm{2}} }}{{\mathop {\rm{p}}\nolimits_{\rm{1}} }}$ (kJ/kgK)
Det kan også vises (sløyfes her) at overført varme (q) er bestemt ved:
q = $\mathop \smallint \limits_1^2 $Tds (kJ/kg) (= flate i Ts-diagrammet)
Ligningen for (q) uttrykker at flater i Ts-diagrammet = overført varme.
Ifølge 2. hovedsetning gjelder at entropien alltid øker for en virkelig prosess. Vi kan derfor si at flater i Ts-diagrammet utgjør enten overført varme eller friksjonsvarme, eller en kombinasjon av disse.
For praktisk bruk gjelder altså følgende sammenheng:
- For strømningsmaskiner (turboladere, dampturbiner, gassturbiner mv.) er massestrømmen så stor at overført varme per kg arbeidsmedium er ubetydelig, herav følger at:
*Flater i Ts-diagrammet ≈ «friksjonsvarme». *
- For stempelmaskiner antar vi tilsvarende at indre friksjonstap er ubetydelige og vi får da at:
Flater i Ts-diagrammet ≈ «overført varme».
Ts- og hs-diagram for gasser
Ts- og hs-diagram for gasser har entropi (s) som horisontal akse og henholdsvis absolutt temperatur i Kelvin og entalpi (h), som regel i kJ/kg, som vertikal akse.
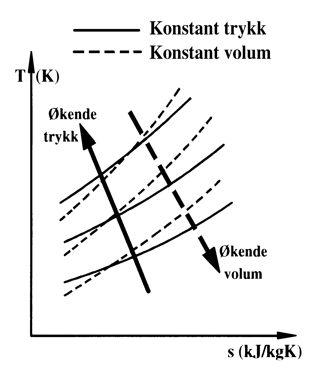
Ts-diagram (ideell gass)
I figuren over er vist et Ts-diagram for gasser.
Linjer for konstant trykk (isobarer) er heltrukne, og linjer for konstant volum (isokorer) er stiplet.
Isobaren har stigning fra 30° til 60°, med linjer for økende trykk oppover mot venstre, som vist med pil på figuren.
Isokoren er "brattere" enn isobaren, med linjer for økende volum nedover mot høyre, som vist med stiplet pil.
For ideell gass er Δh = cp⋅ΔT. Dette innebærer at skisser av prosesser i Ts- og hs-diagrammet blir likeformet, men har forskjellig skala.
Merk derfor at ΔT er en temperaturdifferanse i K, mens Δh er endring av energi i kJ/kg.
For skissering i Ts eller hs diagram kan vi som regel, anta at κ=1,4 som gjelder for luft. Men merk at en isentrop alltid er vertikal, også når (κ) er forskjellig fra 1,4.
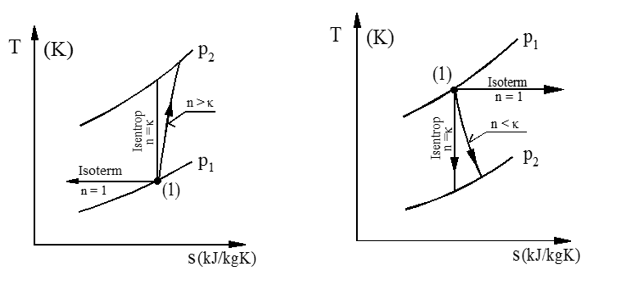
Figuren viser skisse av kompresjon og ekspansjon av gass i Ts-diagram.
Kompresjon Ekspansjon
Merk at for strømningsmaskiner (turboladere, kompressorer og dampturbiner mv.), der vi som nevnt, kan sette q = 0, vil både kompresjons- og ekspansjonskurver alltid «gå» mot høyre i Ts- eller hs-diagram, og flaten under kurven i Ts diagrammet utgjør i prinsippet friksjonsvarme.
Merk videre at ved struping av gass eller damp er entalpien konstant, dvs. «strupelinjer» i hs diagrammet er horisontale.
1.1.4 Kretsprosess og termisk virkningsgrad
Termisk virkningsgrad - definisjon
I en varmekraftmaskin blir varmeenergi omdannet til arbeid ved at arbeidsmediet gjennomgår en kretsprosess, slik det skjer i en motorsylinder eller et dampturbinanlegg.
Termisk virkningsgrad for kretsprosessen er definert ved den andel av tilført varme som blir omdannet til nyttig arbeid:
Termisk virkningsgrad
ηt = $\frac{{Q_t}-{Q_b}}{Q_t}$=$\frac{W(kJ)}{Q_t(kJ)}$=$\frac{W}{{m_B}\bullet{h}}$
Qt = tilført varme (kJ)
Qb = bortført varme (kJ)
W = nyttig arbeid (kJ)
mB = tilført brennoljemengde (kg)
h = brennverdi (kJ/kg)
For stempelmotorer anvender vi to typer termisk virkningsgrad.
Indikert termisk virkningsgrad
ηi = $\frac{{Q_t}-{Q_b}}{Q_t}$=$\frac{P_i}{Q_t}$
Pi = indikert effekt (effekt utviklet i sylinder) (kW)
Qt = $\dot{m}$b(kg/s) ⋅ h(kJ/kg) (= tilført varme) (kW)
Qb = bortført varme (kW)
${\dot{\mathrm{m}}}_{\mathrm{\text{B }}}$= tilført brennstoff mengde (kg/s)
h = brennstoffets brennverdi (kJ/kg)
Indikert termisk virkningsgrad (ηi) gir et mål på hvor stor del av tilført varme med brennstoffet, som omformes til (indikert) effekt eller arbeid i sylinderen.
Effektiv termisk virkningsgrad:
ηe = $\frac{{Q_t}-{Q_b}}{Q_t}$=$\frac{P_e}{Q_t}$
Pe = akseleffekt (kW)
Effektiv termisk virkningsgrad (ηe) gir et mål på hvor stor del av tilført varme som kommer motorens utgående aksel til gode.
Ved å dividere med Pe får vi en alternativ formel for effektiv termisk virkningsgrad:
ηe = $\frac{\mathrm{1}}{\mathrm{b}_{\mathrm{e}}\mathrm{\bullet}\mathrm{\ }\mathrm{h}}$ = ηi ⋅ ηm
be = effektivt spesifikt brennstoff-forbruk (kg/MJ)
h = brennverdi (MJ/kg)
Merk at spesifikt brennstoff-forbruk og termisk virkningsgrad er omvendt proporsjonale.
Brennverdi (h) - definisjon
Brennverdien (h) er den varmemengden (Q) som vi må fjerne fra forbrenningsproduktene etter en fullstendig forbrenning, for å kjøle disse ned til opprinnelig temperatur av luft-/brennstoff- blandingen.
Brennverdien (h) er altså et mål på energiinnholdet i et brennstoff og blir brukt for å beregne tilført varme til ulike maskiner.
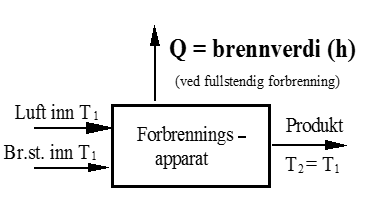
Figuren viser prinsippet for måling av brennverdien.
For faste og flytende brennstoffer oppgir vi vanligvis brennverdien i kJ/kg eller MJ/kg, mens vi for gassformige brennstoffer gjerne bruker kJ per normalkubikkmeter (MJ/nm3).
Måling av brennverdi (1nm3 = 1 m3 ved 0 °C og 1 bar).
Øvre/nedre brennverdi:
Ved forbrenning av hydrogen dannes det vann som på grunn av den høye temperaturen opptrer i dampform. Vannets fordampnings varme er bundet og kan derfor ikke omdannes til arbeid.
For flytende brennstoffer utgjør denne fordampningsvarmen i størrelse ca. 2500 kJ/kg, men er avhengig av mengde hydrogen i brennstoffet.
Det er derfor innført to typer brennverdi, øvre og nedre, der øvre brennverdi inkluderer vannets fordampningsvarme, mens nedre brennverdi er fratrukket denne varmen.
En brennolje som har en øvre brennverdi på 42500 kJ/kg, får dermed en nedre brennverdi på (42500 – 2500) = 40000 kJ/kg.
I SI-systemet er referansetemperaturen for brennverdien satt til 25°C (77°F). På figuren tilsvarer dette at T1 = T2 = 298 K.
I andre sammenhenger bruker vi andre referansetemperaturer, for eksempel 20°C eller 0°C, men forskjellen er uansett ubetydelig for alle praktiske formål.
Merk
Merk at øvre brennverdi er standard i SI-systemet.
Praksis med hensyn til bruk av øvre eller nedre brennverdi er ellers forskjellig fra land til land, men så lenge vi ikke blander begrepene har dette ingen praktisk betydning.
Maksimal termisk virkningsgrad
Mens de fleste virkningsgrader vi bruker i teknikken, har den egenskapen at de ved tekniske forbedringer teoretisk kan nærme seg tallet 1, er dette ikke tilfelle med termisk virkningsgrad.
merk
Ifølge 2. hovedsetning er det nemlig umulig å omdanne en bestemt varmemengde til samme mengde arbeid.
Carnot virkningsgraden
Det største arbeid vi teoretisk kan utvinne mellom to temperaturnivå, oppnår vi ved den såkalte Carnot prosessen. Prosessen har fått navn etter den franske ingeniøren Sadi Carnot, som foreslo den allerede i 1824.
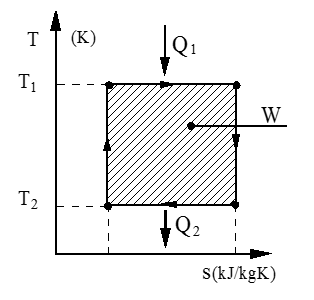
Carnot prosess
Carnot prosessen er definert som en reversibel (tapsfri) kretsprosess, sammensatt av to isotermer og to isentroper, som vist i figuren.
T1 = temperatur ved varmetilførsel (K)
T2 = temperatur ved varmebortføring (K)
Q1 = tilført varme (kJ)
Q2 = bortført varme (kJ)
W = netto arbeid (kJ)
Carnot virkningsgraden:
Carnot virkningsgrad
ηc = $\frac{{\mathop Q\nolimits_1 - \mathop Q\nolimits_2 }}{{\mathop Q\nolimits_1 }}$ = $\frac{{\Delta s \cdot ({T_1} - {T_2})}}{{\Delta s \cdot {T_1}}}$ = 1 − $\frac{{\mathop T\nolimits_2 }}{{\mathop T\nolimits_1 }}$ [1]
Her er T1 temperatur ved varmetilførsel og T2 er omgivelsestemperaturen. Av figuren over ser vi at Δs utgjør to like store entropiendringer og kan derfor strykes i ligningen.
Av [1] følger at termisk virkningsgrad øker dersom (T1) øker og (T2) avtar. Av disse er (T2) bestemt av omgivelsestemperaturen i luft eller vann, som vi i liten grad kan påvirke.
Temperatur for varmetilførselen (T1) kan vi derimot påvirke, idet vi kan oppfatte den som kompresjons- eller forbrenningstemperaturen i for eksempel en dieselmotor.
Ved å øke kompresjonstemperaturen (T1), vil altså termisk virkningsgrad øke. Men i praksis må temperaturen begrenses av flere årsaker, blant annet fordi høy temperatur svekker material- styrken og medfører ofte varmespenninger i godset, som i sin tur kan føre til sprekkdannelser.
Av andre forhold som påvirker temperaturnivået kan vi nevne miljøkrav med hensyn til utslipp av NOx gasser, noe som i praksis innebærer at forbrenningstemperaturen bør holdes under omkring 1500°C dersom vi ønsker å begrense utslippene av NOx gasser.
Termisk virkningsgrad for varmekraftmaskiner kan altså i beste fall nærme seg Carnot- virkningsgraden, men i praksis må vi regne med lavere verdi, blant annet fordi Carnot prosessen forutsetter tapsfrie delprosesser, som i praksis er umulig å realisere.
Carnot prosessen er ellers ikke praktisk gjennomførbar for vanlige varmekraftmaskiner. (Kan imidlertid bli brukt som idealprosess for den såkalte «Stirling» motoren (Svenske ubåter har slike motorer) men denne prosessen blir ikke behandlet i dette kompendiet.
For kulde- og varmepumpeprosesser er derimot Carnot prosessen velegnet som modell for virkelige prosesser. Men merk at kulde- og varmepumpeprosesser går «mot-urs» mens arbeids prosesser alltid går «med-urs».
Anmerkning til maksimal (ηe)
I praksis har store langsomt-gående 2-takts dieselmotorer høyest termisk virkningsgrad av alle varmekraft maskiner og kan ved optimal drift oppnå en effektiv termisk virkningsgrad (ηe) på inntil ca. 52 %. Dette kommer vi tilbake til senere.
1.1.5 Varmeoverføring
Innledning
Problemer i forbindelse med varmeoverføring går igjen i en rekke tekniske oppgaver, de er bestemmende for dimensjonering av kuldeanlegg og kjeler mv. og de dukker opp ved formgivingen av for eksempel støpegods (varmespenninger).
I en varmeveksler er problemet å få overført så stor varmemengde som mulig.
Varme kan overføres på tre prinsipielt ulike måter:
Varmeoverføring
1) Ledning (i faste stoffer, samt stillestående væsker og gasser).
2) Konveksjon (i bevegelige væsker og gasser).
3) Stråling, (dvs. uten noe "bæremedium").
I tillegg nevnes et fjerde prinsipp for varmeoverføring, nemlig fordampning eller diffusjon.
I faste stoffer blir varme overført mest ved ledning, da de fleste faste stoffer er ugjennomtrengelige for varmestråling.
Varmeoverføring ved konveksjon kan skje på to måter:
-
Ved påtvunget strømning blir væsken eller gassen drevet forbi hete- eller kjøleflatene ved hjelp av pumper eller vifter.
-
Ved den frie strømning eller egenkonveksjon oppstår strømningene nettopp som følge av at hete- eller kjøleflaten gir lokale tetthetsendringer, på grunn av lokale temperaturforskjeller.
I tekniske anlegg virker ofte alle tre arter av varmeoverføring sammen, i en dampkjel blir for eksempel varmen fra forbrenningsgassene overført til rørene ved stråling og konveksjon, ved ledning blir varme ført gjennom rørveggen, og ved ledning og konveksjon blir varmen overført til vannet.
Varmeledning
Vi betrakter en plan vegg, og forutsetter stasjonære forhold, dvs. at forholdene ikke endres med tiden. Figuren under viser temperaturforløpet ved stasjonær varmeledning gjennom en plan vegg, der tv1 og tv2 er temperaturene på hver side av veggen.
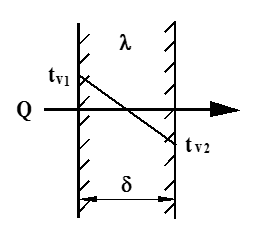
Varmeledning
Varmestrøm
Varmestrøm (Q) gjennom veggen blir:
Q = $\frac{\lambda }{\delta }$ ⋅ A ⋅ (tv1 − tv2) (W)
λ = varmeledningstall (W/mK)
A = veggflate (m2)
δ = veggtykkelse (m)
tv1 = temperatur (varm side) (°C)
tv2 = temperatur (kald side) (°C)
Varmeledningstallet (λ) varierer sterkt for ulike stoff. Elektriske ledere (metaller) leder som regel også varme godt, mens dielektriske stoffer (stein, glass og keramikk) har lav varmeledningsevne. Porøse stoffer, tre, tøy, glassvatt og skumplast leder varme meget dårlig, fordi luft som fyller porene er en dårlig varmeleder.
Tabellen viser varmeledningsevnen (λ) i (W/mK) for noen stoff
| Stoff | Varmeledningsevne W/mK |
|---|---|
| Sølv | 418 |
| Glass | 0,7 - 1,0 |
| Kobber | 398 |
| Granitt | 2,0 - 4,0 |
| Stål | 45 |
| Betong | 0,3 - 1,0 |
| Is | 2,2 |
| Papir | 0,12 - 0,3 |
| Vann | 0,6 |
| Luft | 0,025 |
Eksempel
Eksempel varmeledning
En 3 mm tykk metallplate med varmeledningstall (λ) = 17,3 W/mK skiller to vannmengder. Platens temperatur er 55°C på den ene siden og 20°C på den andre. Bestem varmestrøm gjennom 1 m2 av platen.
Q = $\frac{\lambda }{\delta }$ ⋅ A ⋅ (tv1 − tv2) = $\frac{17,3 \text(W/mK)}{0,003 (m)}$⋅ 1(m2) ⋅ (55 − 20)(°C) = 202 kW
Varmegjennomgang, k - verdi
For de fleste varmevekslere kjenner vi ikke skilleveggens overflatetemperaturer, men bare fluidtemperaturen på begge sider. I figuren under er vist temperaturforløpet ved samtidig konveksjon og ledning gjennom en plan vegg.
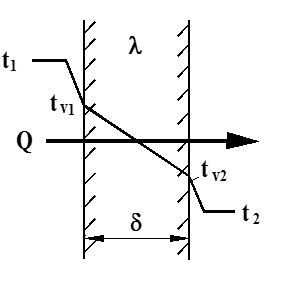
Overført varme kan uttrykkes ved følgende tre ligninger:
Overført varme
Varmeovergang fra fluid til vegg:
Q = α1⋅ A ⋅ (t1 – tv1) (W) [1]
α = varmeovergangstall (W/m2K)
Varmeledning gjennom veggen:
Q = $\frac{\lambda }{\delta }$ ⋅ A ⋅ (tv1 – tv2) (W) [2]
Varmeovergang fra vegg til fluid:
Q = α2 ⋅ A ⋅ (tv2 – t2) (W) [3]
Av [1], [2] og [3] får vi:
Q = k ⋅ A ⋅ (t1 − t2) (W)
k =$\frac{1}{{\frac{1}{{{\alpha _1}}} + \frac{\delta }{\lambda } + \frac{1}{{{\alpha _2}}}}}$ = varmegjennomgangstall (W/m2K)
Varmeoverføring i varmevekslere
Medstrøm varmeveksler
I det foregående har vi behandlet varmeutveksling mellom to væsker (eller gasser) atskilt fra hverandre ved en vegg, under den forutsetning at temperaturen på begge sider av veggen var konstant. I de fleste varmevekslere endrer temperaturen seg for begge fluid, og vi må da regne med en midlere temperaturdifferanse.
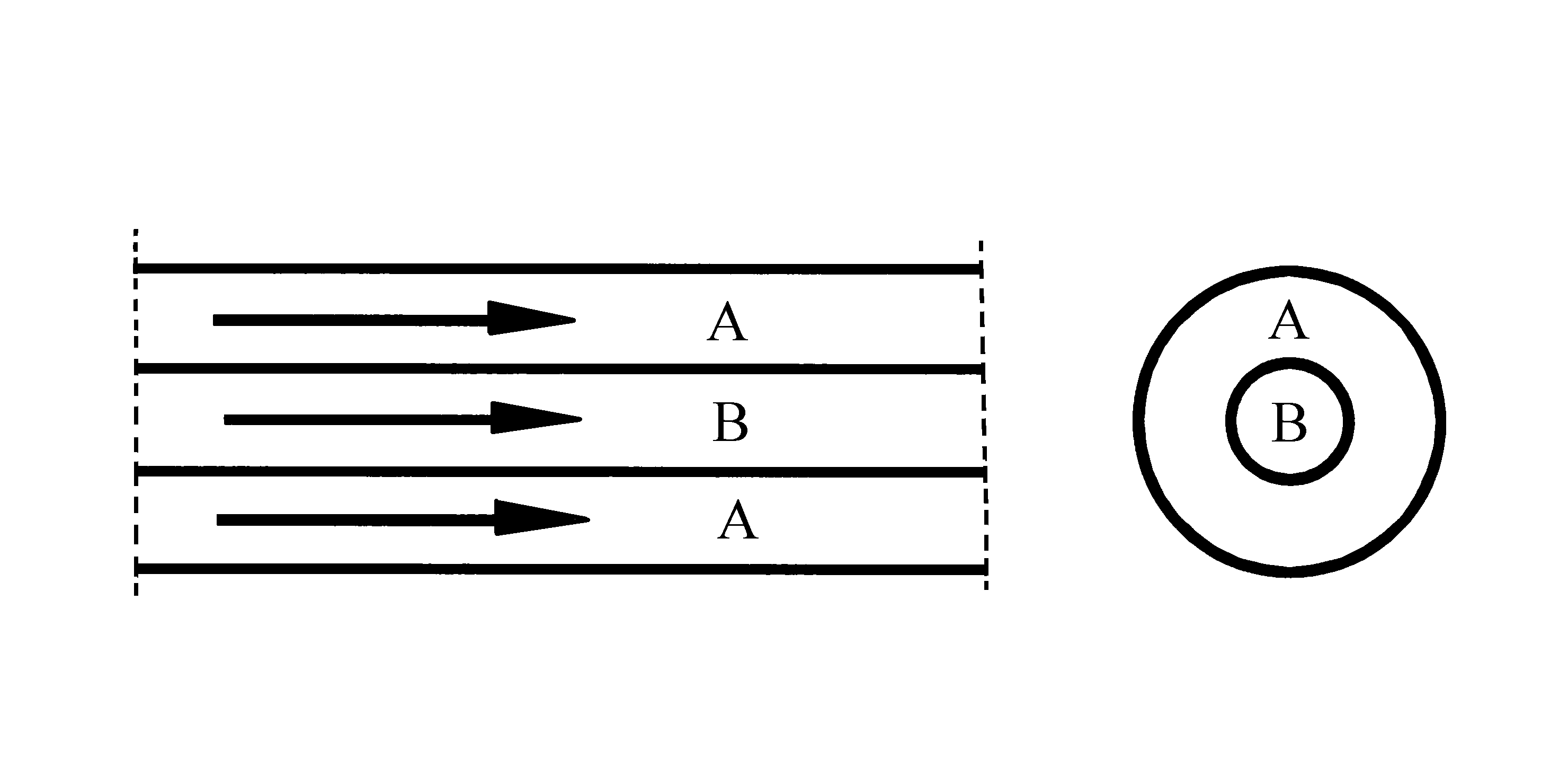
Medstrøms varmeveksler, forenklet
Figuren viser en varmeveksler, der begge fluid føres inn fra samme ende av to konsentriske rør. Dette kaller vi medstrøms arrangement.
Midlere temperaturdifferanse mellom fluidene kan vi beregne på flere måter, men mest brukt er den såkalte midlere logaritmiske temperaturdifferanse, ofte kalt MLTD.
Neste figur viser temperaturforløpet for medstrøms arrangement.
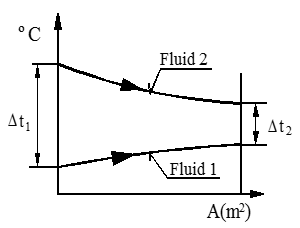
Temperaturdiagram for medstrøms arrangement
Overført varme (Q):
Overført varme (Q):
Q = k ⋅ A ⋅ Δtm (W)
Δtm = $\frac{{\Delta \mathop t\nolimits_1 - \Delta \mathop t\nolimits_2 }}{{ln\frac{{\Delta \mathop t\nolimits_1 }}{{\Delta \mathop t\nolimits_2 }}}}$ (K)
Δtm = MLTD (K)
Δt1 = temperaturforskjell innløp i °C
Δt2 = temperaturforskjell utløp i °C
NB!
Formelen for (Δtm) eller MLTD inneholder som vi ser, en «naturlig» logaritmefunksjon, derav navnet midlere logaritmisk temperturdifferanse. Funksjonen fremkommer ved matematisk utledning av midlere temperaturdifferanse mellom to fluid, og vi kan oppfatte den som en form for midlere temperaturdifferanse.
Som kontroll ved beregninger kan vi derfor si at MLTD må ligge et sted mellom største og minste temperaturdifferanse.
Motstrøm varmeveksler
En annen mulighet for føring av væsker i en varme-veksler er motstrøm, se figur. Men merk at formler for overført varme og midlere logaritmisk temperaturdifferanse er like for med- og motstrøms varmevekslere.
Overført varme (Q):
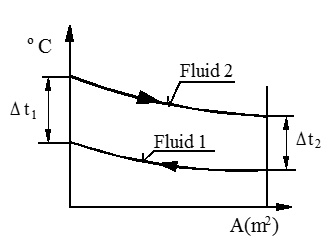
Temperaturdiagram for Motstrøms-arrangement
Q = k ⋅ A ⋅ Δtm (W)
Δtm = $\frac{{\Delta {t_1} - \Delta {t_2}}}{{{\rm{ln}}\frac{{\Delta {t_1}}}{{\Delta {t_2}}}}}$ (K)
Δtm = MLTD (K)
k = varmegjennomgangstall (W/m2K)
A = areal (m2)
Ved motstrømsarrangement kan det forekomme at (Δt1) er lik, eller nesten lik (Δt2). Formelen for (Δtm) gir da et ubestemt uttrykk, (null over null) som ikke gir mening. I slike tilfeller kan vi anvende følgende formler:
Aritmetisk middeltemperaturdifferanse
ΔtM = $\frac{{\Delta \mathop t\nolimits_1 + \Delta \mathop t\nolimits_2 }}{2}$ (K)
Eller:
Δtm = $\sqrt{\mathrm{t_1}}\cdot{\mathrm{t_2}}$
En tredje mulighet for føring av væsker i en varmeveksler er kryss-strøm, der fluidene blir ført på tvers av hete- eller kjøleflaten. Forholdene blir da mer komplekse og vi må da beregne midlere temperaturdifferanse ved hjelp av empiriske formler. Tas ikke med her.
Generelt gjelder at motstrømsarrangement gir mindre kjøler-areal enn medstrøms arrangement, mens kryss-strøm ligger et sted mellom disse. I praksis tilstreber vi derfor motstrømsarrangement dersom ikke andre forhold hindrer dette.
Eksempel - Varmeveksler
Eksempel - Varmeveksler
I en varmeveksler kjøles olje fra 70 °C til 40 °C i motstrøm av ferskvann med temperatur inn på 20 °C og ut 60 °C. Massestrøm olje er 4 kg/s, colje = 1,9 kJ/kgK, k = 0,52 kW/m2K.
Bestem:
a) Midlere logaritmisk temperaturdifferanse.
b) Overført varme i kW.
c) Nødvendig kjøleflate og massestrøm vann.
Skisse av temperaturforløpet:
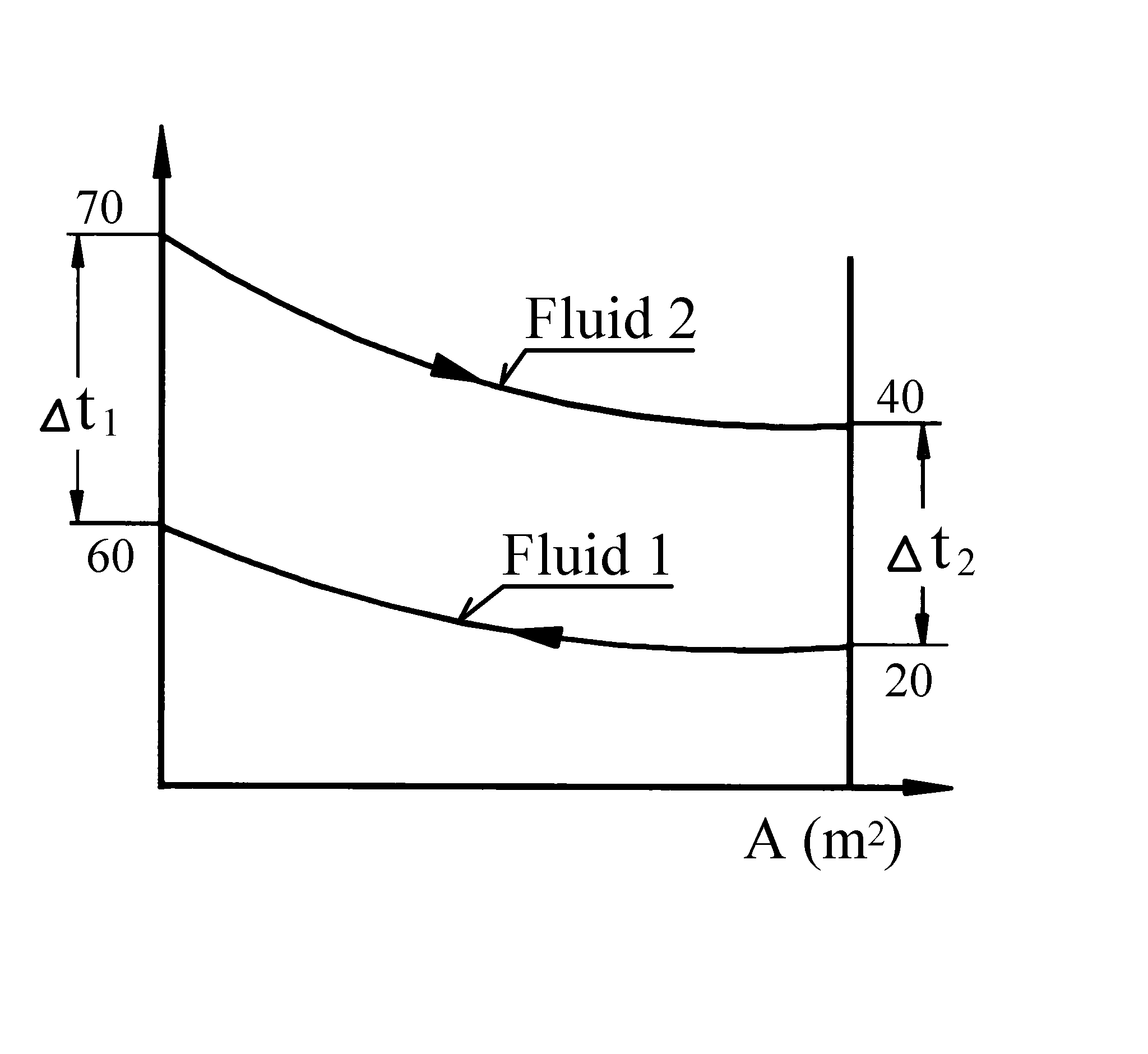
a) Temperatur differanser:
Δt1 = 70 − 60 = 10 °C
Δt2 = 40 − 20 = 20 °C
Δtm = $\frac{{\Delta \mathop t\nolimits{_1} - \Delta \mathop t\nolimits{_2}}}{{ln\frac{{\Delta \mathop t\nolimits_1}}{{\Delta \mathop t\nolimits_2}}}}$ = $\frac{{10 - 20}}{{ln\frac{{10}}{{20}}}}$ = 14,4 °C
b) Overført varme:
Q = m ⋅ o ⋅ co ⋅ Δto = 4(kg/s) ⋅ 1,9(kJ/kgK) ⋅ (70 − 40)(K) = 228 kW
c) Kjøler areal (A):
Q = k ⋅ A ⋅ Δtm ⇒
A = $\frac{Q}{{k \cdot \Delta {t_m}}}$ =$\frac{\mathrm{228(kW)}}{{0,52}\mathrm{{kW}/m^2K)}\cdot{\mathrm{14,4(K)}}}$ = 30,5 m2
Vi har at: Q = $\dot{m}(\frac{\text{kg}}{s})$ ⋅ cvann~ (kJ/kgK) ⋅ Δt~vann(K) og får:
Massestrøm vann $\dot{\mathrm{m}}$ = $\frac{Q}{{{c_v} \cdot \Delta {t_v}}}$ = $\frac{\mathrm{228(kW)}}{\mathrm{4,2({kJ/kgK}}) \cdot \mathrm{(60 - 20)K}}$ = 1,35 kg/s
1.1.6 Fuktig luft
Innledning
Kroppens temperaturbalanse blir opprettholdt ved at vann fordunster fra huden (og under anstrengelse ved svetting). Størrelsen av denne avdunsting er sterkt avhengig av luftfuktigheten, som derfor har stor betydning for vårt velvære.
Også for maskineri er luftfuktigheten av stor betydning, spesielt gjelder dette for dieselmotorer som krever relativt stor luftgjennomgang. For metalliske materialer er det særlig korrosjonsfaren som har betydning, mens det for elektriske anlegg er isolasjonsmotstanden som blir påvirket.
Relativ fuktighet
Fuktighet i luft kan angis på flere måter, for eksempel som fuktighetsgrad (x) i gram vann per kg tørr luft.
En annen og mer vanlig betegnelse er relativ fuktighet (ϕ):
ϕ = $\frac{{\mathop p\nolimits_D }}{{\mathop p\nolimits_m }}$
pD = vanndampens virkelige partialtrykk i lufta (Pa)
pm = vanndampens metningstrykk (Pa)
Ved relativ fuktighet (ϕ) = 1 er luften mettet med vanndamp.
Forholdet pD/pm er ellers omtrent lik forholdet mellom virkelig fuktighetsgrad i luften og fuktighetsgrad for mettet luft ved samme temperatur.
ϕ = $\frac{{{p_D}}}{{\mathop p\nolimits_m }}$ $ \approx $ $\frac{{{x_1}}}{{{x_m}}}$
x1 = virkelig vanninnhold i g/kg ved tilstand (1)
xm = vanninnhold for mettet luft ved samme temperatur (t1)
En fuktighetsgrad på for eksempel 0,8 vil altså tilsvare en relativ fuktighet på ca. 80 %. I praksis bruker vi derfor begge begrepene om hverandre.
Mollier diagram for fuktig luft
Figuren under viser et Mollier-, også kalt h-x diagram for fuktig luft. Diagrammet har temperatur i °C langs vertikalaksen og vanninnhold x i g/kg tørr luft langs horisontalaksen. Metningslinjen er grensen for hvor mye vann luften kan inneholde, dvs. relativ fuktighet (ϕ) = 1. Over metningslinjen finner vi linjer for varierende relativ fuktighet (ϕ). Linjer for konstant entalpi (h) går på skrått oppover (mot venstre) i diagrammet.
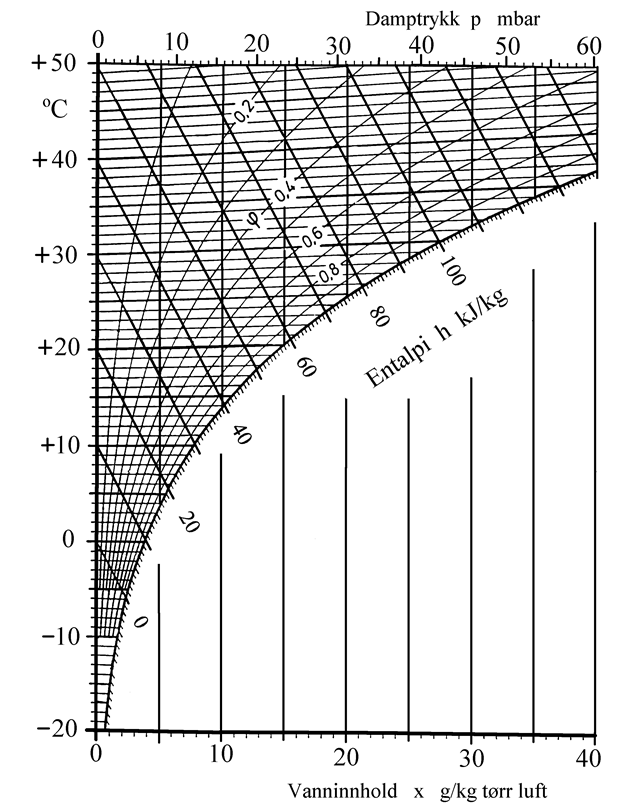
Mollier diagram for fuktig luft
Duggpunkt
Duggpunktet, eller duggpunktstemperaturen er den temperaturen luften har når den ved avkjøling, begynner å skille ut vann.
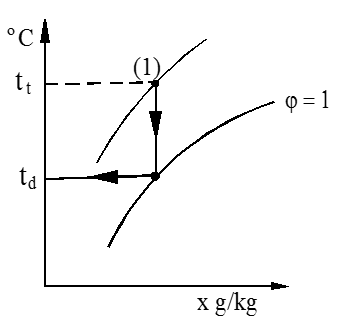
I h-x diagrammet finner vi duggpunktet ved å trekke en vertikal linje fra tilstandspunkt (1) ned til skjæring med metningslinjen, som vist i figuren.
Duggpunktstemperaturen (td) kan vi deretter avlese som vist på figuren.
Merk at luftens vanninnhold (x) ikke endres under avkjølingen.
Duggpunkts-bestemmelse
Eksempel – Duggpunkts-bestemmelse
En luftmengde har tørr temperatur på 22°C og relativ fuktighet (ϕ) = 0,5 og vi ønsker å bestemme luftens duggpunkt.
(Merk at tørr temperatur tt er lufttemperaturen målt med et vanlig termometer).
Vi bruker Mollier-diagram for fuktig og går frem som vist i figuren over.
-
Først avsettes tilstandspunkt (1) i diagrammet,
-
deretter trekker vi en vertikal linje ned til skjæring med metningslinjen.
I eksempelet avleser vi duggpunktstemperaturen (td):
td ≈ 11°C
Fukting av luft
Fukting av luft kan foregå ved at vi enten sprøyter inn vann eller vanndamp. Om vi tilfører (mw) kg vann med entalpi (hw), til (mL) kg luft, finner vi vanninnhold og entalpi av:
Vanninnhold: xbl = x1 + $\frac{{\mathop m\nolimits_w }}{{\mathop m\nolimits_L }}$ (1)
Entalpi: hbl = h1 + $\frac{{\mathop m\nolimits_w \cdot \mathop h\nolimits_w }}{{\mathop m\nolimits_L }}$ (2)
Ligning (2) skrevet som differensialligning:
dhbl = d $\left( {\frac{{{m_w}}}{{{m_L}}}} \right)$hw = dx ⋅ hw ⇒ $\frac{{dh}}{{dx}}$ = hw (3)
Av ligning (3) følger at luftens tilstandsendring må foregå langs en rett linje med stigning bestemt ved:
$\frac{{dh}}{{dx}}$= hw = spesifikk entalpi for tilført vann eller damp.
Når vi tilfører vann (i dråpe-form) er entalpien av tilført vann (mw⋅hw) svært liten i forhold til luftens entalpi og vi kan derfor anta at tilstandsendringen foregår ved konstant entalpi. Slike forhold vil vi ha når vann blir tilført i dråpe-form, f.eks. ved bruk av en luft-fukter.
Når vi tilfører vann i dampform, vil tilført entalpi også bestå av vannets fordampningsvarme. Da vannets fordampningsvarme er relativt høy (ca. 2500 kJ/kg), vil blandingens entalpi øke merkbart. Luftens tilstandsendring vil da foregå langs en rett linje parallelt med vanndampens entalpilinje i Mollier-diagrammet.
Anmerkning
Noen h-x diagram for fuktig luft har slike entalpilinjer inntegnet langs ytterkanten av diagrammet. Tilstandsendringens "retning" blir altså parallell med disse entalpilinjene.
Eksempel - Luftfukting
Eksempel - Luftfukting
Luft med temp. t = + 30°C og relativ fuktighet ϕ = 0,4 passerer en luft fukter og mettes med vann. Bestem (våt) temperatur etter befuktning og tilført vannmengde.
Fra tilstandspunktet: t = 30°C og ϕ = 0,4 føres en linje parallelt med h = konstant - linjen til skjæring med metningslinjen. I skjæringspunktet avleser vi temperaturen tvåt = + 20°C.
Vanninnholdet avleses på horisontalskalaen til x1 = ca. 10,8 g/kg før befuktning og x2 = 14,8 g/kg etter befuktning. Tilført vannmengde blir:
Δx = x2 − x1 = 14,8 − 10,8 = 4 g/kg
Eksempel - Fukting av luft med vann/damp
I en luftstrøm på 1000 kg/h med temperatur t1 = 22°C og ϕ = 30 %, blir tilført 2 kg vann/h med temperatur tw = 15°C.
a) Hva blir blandingstilstanden?
b) Hva blir blandingstilstanden dersom vi isteden for vann sprøyter inn en like stor mengde tørrmettet damp av 1 bar (h = 2675 kJ/kg).
a) Vanninnsprøyting
hw = cw ⋅ (tw − 0) = 4,18 kJ/kg ⋅ (15 − 0) = 62,7 kJ/kg
xbl = 0,0048 + $\frac{2}{{1000}}$ = 0,0068 kg vann per kg tørr luft
hbl = 34 + $\frac{{2 \cdot 62,7}}{{1000}}$ ≈ 34 kJ/kg
(Merk at vannets entalpi er ubetydelig i forhold til luftens entalpi og kan derfor sløyfes).
Vi går ut fra start tilstanden: t1 = 22°C og ϕ1 = 0,3 og tegner en linje parallelt med h = konstant- linjen (på skrå nedover mot høyre). Videre vet vi at blandingstilstanden må ligge et sted på denne entalpilinjen. Vi trekker derfor en vertikal linje gjennom xbl = 6,8 g/kg til den skjærer entalpilinjen.
I h-x diagrammet avleser vi:
tbl = 17,5°C og ϕ = 55 %
Ved innsprøyting av vann synker altså blandingstemperaturen. Dette har sin forklaring i at den varmen som skal til for å fordampe vannet (fordampningsvarmen) er tatt fra lufta, mens den varmen som blir tilført med vannet er ubetydelig og kan som nevnt, utelates.
b) Dampinnsprøyting
Ved innsprøyting av samme mengde damp blir blandingens vanninnhold uforandret, dvs.:
xbl = 0,0068 kg/kg
Blandingens entalpi: hbl = 34 + $\frac{{2 \cdot 2675}}{{1000}}$ ≈ 39,5 kJ/kg
Av h-x diagrammet avleses:
tbl = 22,5°C og ϕ ≈ 40 %
Ved innsprøyting av damp øker altså lufttemperaturen. Dette kan vi forklare ved at vannets fordampningsvarme blir tilført luften, som derved blir oppvarmet.
Vannutfelling i motorer
Ved atmosfæretrykk inneholder luft i størrelse 0,01 - 0,02 kg vann per kg luft. Om vi for eksempel betrakter en stor dieselmotor på omkring 100 000 kW, så har den en luftgjennomgang på omkring 100 000 kg/h, dvs. vannmengden i luften utgjør mellom 1000 og 2000 kg/h. I tillegg kommer vann som blir dannet ved forbrenning av hydrogen i brennoljen.
Ved lav belastning, dvs. lave godstemperaturer er det fare for at deler av dette vannet kondenserer på foringen, noe som igjen kan føre til at smøreoljefilmen på foringen vaskes bort og at det oppstår korrosjon på foringen, særlig ved drift på tungolje.
Ved drift på tungolje vil svovel i oljen reagere med oksygen til svoveldioksid, en del av denne reagerer videre til svovel trioksid som sammen med fuktighet danner svovelsyregass.
Merk at på grunn av det høye trykket i sylinderen er duggpunktstemperaturen relativt høy, opptil 150°C.
For å unngå driftsproblemer med hensyn til korrosjon, bort-vasking av smøreoljefilmen på sylindervegger mv., bør vi derfor alltid holde spylelufttemperaturen over luftens dugg-punkts temperatur.
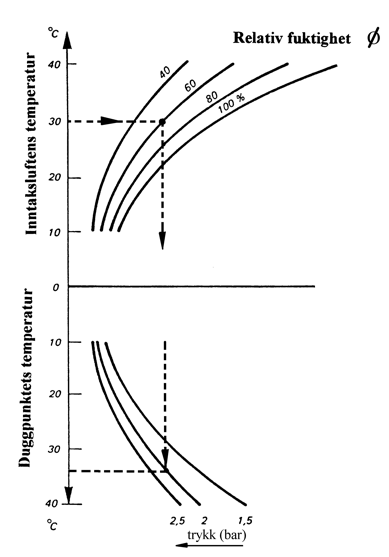
Figuren over viser eksempel på et hjelpediagram til å finne duggpunktet for spyleluften.
Eksempel
Innsugsluft: t = 30°C.
Relativ fuktighet ϕ = 60%.
Spyletrykk = 2 bar.
Vi avleser da duggpunktet (td) til:
td ≈ 34 °C
Om vi kjøler luften under 34°C, vil det altså bli felt ut vanndråper i spyle- systemet.
For å ha en viss margin mot vann- utfelling, er det vanlig praksis å kjøle spyleluften til omkring 5 - 10°C over duggpunktstemperaturen.
Typisk spylelufttemperatur er derfor omkring 45 til 50°C.
Vannutfelling i trykkluftsystem
Det er som nevnt, alltid en viss mengde vann i luften. Dette vannet er også tilstede i komprimert luft. Når vi for eksempel bruker komprimert luft i trykkluftverktøy, vil gjenværende luft i tanken ekspandere til et lavere trykk, og temperaturen vil derfor synke.
Da kald luft kan inneholde mindre vann enn varm luft, blir derfor en del vann kondensert. Dette kan igjen føre til at smøremidlet i verktøyet blir vasket bort. Dersom temperaturen synker til under 0°C, kan det også oppstå isdannelse i verktøyet.
Eksempel - Vannutfelling
Eksempel - Vannutfelling
Om vi for eksempel komprimerer luft av 20°C med relativ fuktighet (ϕ) = 0,4, så inneholder den ca. 6,5 g/m3.
Dersom denne luften blir komprimert til 800 kPa og deretter får kjølne til 20°C etter kompresjonen, vil det nye volumet være ca. 1/8 av det opprinnelige.
Dette innebærer at 1 m3 luft med trykk 800 kPa vil inneholde: 8 ⋅ 6,5 = 52 g vann. Men luft av 20°C kan inneholde høyst ca. 18 g vann per m3, da er den mettet. Forskjellen (52 − 18 = 34 g), blir altså felt ut eller kondensert i trykklufttanken.
Dersom temperaturen synker ytterligere ved fortsatt bruk, vil det bli kondensert ut enda mer vann.
For å unngå driftsforstyrrelser bør det derfor monteres kondensutskillere på passende steder i et trykkluftsystem.
Noter
[^1]: Merk at for væsker er cp = cv
[^2]: Omforming krever arbeid.
[^3]: Entropi er per definisjon et mål på uorden i et system.

