1.3 Hydromekanikk
1.3.1 Trykk (p)
Trykk er forholdet mellom kraft som virker loddrett inn mot en flate og arealet av flaten.
Vi skriver dette slik:
p = $\frac{F}{A}$ (kPa)
Der p er trykket i kPa, F er kraften i kN og A er arealet i m2.
Trykket kan virke mot overflaten av et legeme eller mot en tenkt flate i legemets indre. I væsker og gasser vil det alltid være et visst trykk. Men om en gass får utvide seg ubegrenset, går trykket mot null.
Trykket over en væske eller i en væske kan bare reduseres til væskens damptrykk ved den temperatur væsken har. Det vil da inntre koking slik at væsken går over i dampform.
I SI - systemet måler vi trykk i pascal, 1 Pa = 1 N/m2. Denne enheten er relativt liten og derfor lite anvendelig i teknisk sammenheng. I praksis anvender vi derfor avledete enheter, som for eksempel: MPa = 106 Pa, kPa = 103 Pa og bar = 105 Pa.
De fleste trykkmåleinstrument måler trykket over atmosfæretrykket, såkalt manometertrykk eller overtrykk. Absoluttrykket er derfor lik:
pabs = patm + pman
Figuren under viser sammenhengen mellom absolutt-, atmosfære- og manometertrykk.
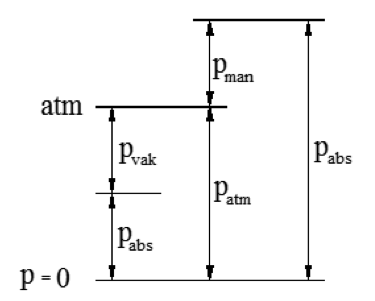
Trykk
pabs = absolutt trykk (Pa)
patm = atmosfæretrykk (Pa)
pman = manometertrykk (Pa)
Trykk lavere enn atmosfæretrykket kaller vi vakuum. Vi har altså:
patm = pvak + pabs (Pa)
pvak = vakuum (Pa)
Atmosfæretrykket er ikke konstant, men varierer med tiden og hvor vi befinner oss. En mye brukt referanseverdi er en standard atmosfære, definert som tyngdetrykket av en kvikksølvsøyle (Hg) på 760 mm ved 0°C. (1 atm = 1,013 bar), eller 750 mm Hg ved 0°C (750 mm Hg = 1 bar).
Hydrostatisk- og dynamisk trykk
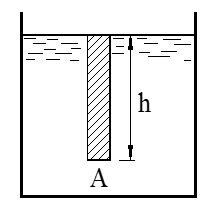
Tyngdetrykk
Hydrostatisk trykk eller tyngdetrykket i en væske er kraft per flateenhet på grunn av væskens tyngde. Tyngdetrykket på flaten (A) i figuren under er lik tyngden av den skraverte væskesøylen:
p = $\frac{\mathrm{F}}{\mathrm{A}} = \frac{\mathrm{\text{ρAhg}}}{\mathrm{A}}\ $= ρgh (Pa)
ρ = tetthet (kg/m3)
g = tyngdeakselerasjon (m/s2)
h = væskesøyle høyde (m)
Tyngdetrykket er like stort i alle retninger. Trykket er derfor uavhengig av flatens skråstilling, så fremt høyden h er målt fra overflaten av væsken til flatens tyngdepunkt.
Trykk måles også i væskesøylehøyde (hs):
hs = $\frac{p}{{\rho \cdot g}}$ (m)
hs = trykk i meter væskesøyle
p = trykk (N/m2)
Dynamisk trykk
For væsker og gasser i bevegelse måler vi statisk trykk vinkelrett på strømningsretningen, mens dynamisk trykk blir målt mot strømningsretningen, se figur.
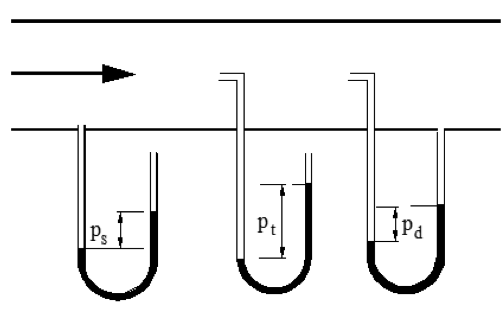
Statisk-, total- og dynamisk trykk
Totaltrykk ptot = pstat + pdyn
pt = totaltrykk (Pa)
ps = statisk trykk (Pa)
pdyn = dynamisk trykk (Pa)
pdyn = ${\frac{\rho }{2}}$⋅ c2
ρ = tetthet (kg/m3)
c = hastighet (m/s)
Hydrostatisk trykk mot tank-flater
Trykket i en væske som er i ro er kjennetegnet ved at:
- Trykket i et punkt er like stort i alle retninger.
- Trykket virker alltid vinkelrett på flaten.
Det hydrostatiske trykket mot bunnen i de to karene a) og b) på figuren under er like stort i begge karene. Dersom bunnarealene er like store, blir kreftene som trykker mot bunnene også like store.
Mot bunnen får vi altså trykkraften (F):
F = p(N/m2) ⋅ A(m2) = ρ ⋅ g ⋅ h ⋅ A (N)
A = areal (m2)
p = ρ(kg/m3) ⋅ g(m/s2) ⋅ h(m)
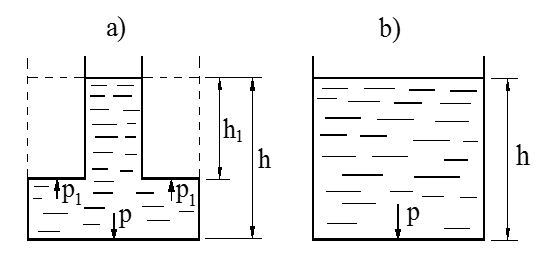
Trykk mot tankflater
Trykkraften mot tanktoppen i kar a) blir:
F1 = p1(N/m2) ⋅ A1(m2)
A1 = areal av tanktopp (m2)
p1 = ρ(kg/m3) ⋅ g(m/s2) ⋅ h1(m)
Eksempel – hydrostatisk trykk
Bestem det hydrostatiske trykket 30 m under overflaten av en væske når tettheten er 1030 kg/m3 og g = 9,8 m/s2?
p = ρ ⋅ g ⋅ h = 1030(kg/m3) ⋅ 9,8(m/s2) ⋅ 30(m) $ \approx $ 3⋅105 Pa = 3 bar
Trykkprøving av tanker
Vi trykkprøver tanker for å kontrollere om tanktoppen vil tåle trykket ved overfylling eller at tanktoppen i dobbeltbunnen av et skip tåler væsketrykket dersom bunnen skulle bli lekk, for eksempel ved grunnstøting. Fremgangsmåten er i korthet som følger:
Vi fyller vann i tanken og påfyllingsrøret til godt over laveste vannlinje.
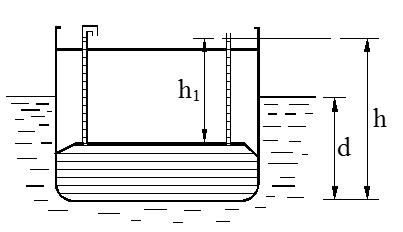
Trykkprøving av tank
Kraften oppover mot tanktoppen er da lik produktet av tanktoppens areal og det hydrostatiske trykket på grunn av høyden h1:
F1 = ρgh1 ⋅ A1 (N)
F1 = kraft mot tanktopp (N)
h1 = væskesøylehøyde over tanktopp (m)
A1 = tanktoppens areal (m2)
ρ = væskens tetthet (kg/m3)
Eksempel – Trykkprøving av tank
En rektangulær bunntank har lengde 12 m, bredde 8 m og høyde 0,8 m. Væsken står 7 m opp i peilerøret (over tankens bunn).
Bestem kraften fra væsken mot tankens bunn og topp når væskens tetthet er 1025 kg/m3.
Tankens bunn- og toppareal: A =12 ⋅ 8 = 96 m2
Kraft mot bunnen (FB):
FB = ρgh ⋅ A = 1025 (kg/m3) ⋅9,8(m/s2) ⋅7(m) ⋅ 96(m2)
FB = 6,76 ⋅ 106 N = 6,76 MN
Kraft mot tanktopp (FT):
FT = ρgh1 ⋅ A = 1025(kg/m3) ⋅ 9,8(m/s2) ⋅ 6,2(m) ⋅ 96(m2)
FT = 5,98 ⋅ 106 N = 5,98 MN
Hydraulisk trykkraft
Det faktum at trykket i en væske i en lukket beholder forplanter seg like sterkt i alle retninger, utnytter vi ved en hydraulisk presse. I figuren under er vist prinsippet for en slik hydraulisk presse.
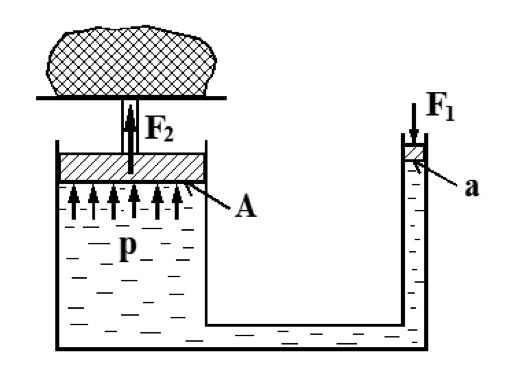
Hydraulisk presse
Det lille pumpestempelet presser olje under det store presstempelet. Derved oppnår vi en kraftvinning.
Vi har at trykket er like stort under begge stempler og får:
p = $\frac{{{F_2}}}{A}$ = $\frac{{{F_1}}}{a}$ (Pa)
Herav får vi presskraften (F2):
F2 = F1 ⋅ $\frac{A}{a}$ (N)
F1 = kraft på pumpestempel (N)
A = areal av presstempel (m2)
a = areal av pumpestempel (m2)
Eksempel – hydraulisk trykkraft
Eksempel – hydraulisk trykkraft
Ved en hydraulisk presse som vist i figuren over, er pumpestempelets areal a = 20 cm2 og press- stempelets areal A = 1600 cm2. Bestem kraften F2 på presstempelet når kraften F1 på pumpestempelet er 500 N.
Presskraft F2 = F1 ⋅ $\frac{A}{a}$ = 500(N) ⋅$\frac{{1600}}{{20}}$ = 40000 N = 40 kN
Kort om hydrauliske system
I hydrauliske systemer blir den mekaniske energien som utgjør energiforsyningen til systemet, først og fremst omformet til hydraulisk energi, som i sin tur, blir omformet til hydraulisk energi, som i sin tur blir overført og styrt, for til slutt igjen å bli omformet til mekanisk energi. Dette skjer ved hjelp av hydrauliske komponenter som er ordnet slik at de virker sammen etter en på forhånd innstilt sekvens slik at de utfører den den ønskede funksjonen.
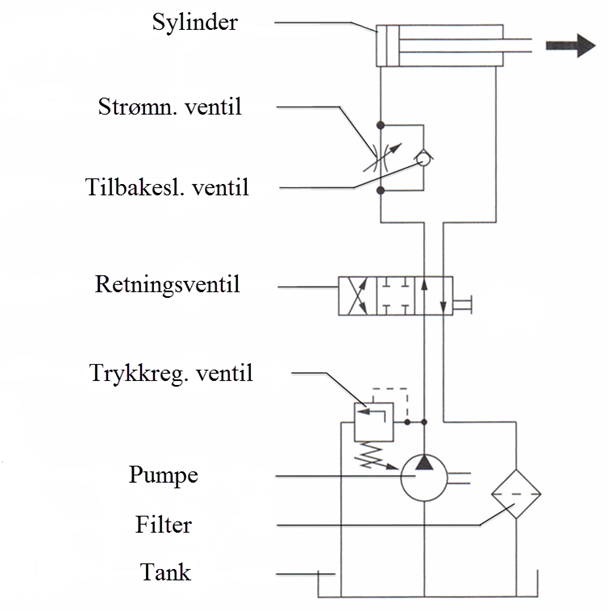
Figuren viser et grunnleggende hydraulisk system og de komponentene som inngår i systemet.
Retningsventilen
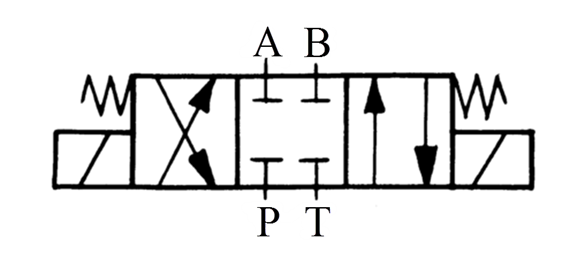
Den viste ventilen har tre posisjoner og fire rørtilkoblinger, og benevnes derfor ¾-ventil. I midtposisjon er alle fire tilslutningene stengt. Når spindelen skyves mot høyre, blir det forbindelse mellom P-B og A-T. Skyves den til venstre, blir forbindelsene P-A og B-T.
Koblet i en sylinder-krets står sylinderen stille når ventilen er i midtposisjon. Med ventilen aktivert styres oljestrømmens retning slik at sylinderen beveger seg
De tre firkantene symboliserer koblingsmulighetene mellom A, B, P og T. For å forstå slike hydraulikksymboler må vi tenke oss at tilkoblingene står stille, og at blokken med pilene skyves i samme retning som spindelen. I dette tilfellet er ventilen elektrisk operert, indikert av magnetventil symbolene på side
1.3.2 Innvendig trykkbelastning i rør og beholdere
Radielle spenninger i rør og beholdere
Vi vil bestemme spenningene i rør og sylindriske beholdere utsatt for et innvendig overtrykk.
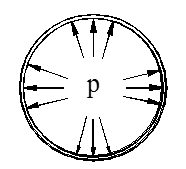
Innvendig trykk
Gassen eller væsken utøver et tilnærmet jevnt fordelt trykk (p) mot rør- eller beholderveggen som blir utsatt for strekk.
Hvis trykket er stort nok blir røret/beholderen sprengt utover. Styrken i materialet må derfor kunne stå imot de kreftene som skyldes overtrykket i røret.
For å studere dette nærmere tenker vi oss at vi snitter røret (beholderen) på midten og påfører de krefter som virker på den avkappede halvdelen, se figuren under.
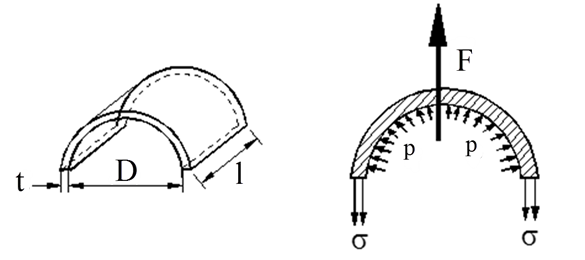
Samlet vertikal kraft F på en rør- eller beholderlengde på l m blir lik samlet trykk-kraft mot den innvendige flatens vertikalprojeksjon (D ⋅ l).
Vi får angrepskraften F:
F = p(Pa) ⋅ D(m) ⋅ l(m) (N) [1]
Denne kraften vil materialet i de 2 rør- eller beholderveggene mobilisere krefter mot. Samlet kraft nedover utgjør derfor mobilisert spenning ganger «strukket» areal:
F = 2 ⋅ σ(Pa) ⋅ t(m) ⋅ l(m) (N) [2]
Vi setter [1] = [2] og får opptredende spenning (σ):
σ = $\frac{{pD}}{{2t}}$ (Pa) eller tnødv = $\frac{{p \cdot D}}{{2 \cdot {\sigma _{till}}}}$ (m) [3]
Her er tnødv = nødvendig godstykkelse i meter.
Eksempel 1
En sylindrisk beholder av stålplater skal tåle et innvendig trykk p = 10 bar og ha en innvendig diameter D = 1 m.
Tillatt strekkspenning i stålplaten er σtill = 120 N/mm2.
Bestem nødvendig godstykkelse.

Innsetting i ligning [3] gir nødvendig godstykkelse:
tnødv = $\frac{{p \cdot D}}{{2 \cdot {\sigma \_{till}}}}$ = $\frac{{{{10}^6}(Pa) \cdot 1(m)}}{{2 \cdot 120 \cdot {{10}^6}(Pa)}}$
tnødv = 4,17 ⋅ 10−3 m = 4,17 mm
Beregnet godstykkelse er altså 4,17 mm og beholderen bør derfor lages av 5 mm plater.
Eksempel 2
En sylindrisk beholder har innvendig trykk p = 1,2 N/mm2 og diameter D = 1,4 m.
Tillatt spenning σtill = 90 N/mm2.
Bestem nødvendig godstykkelse.
Ligning [3] gir nødvendig godstykkelse:
tnødv = $\frac{{p \cdot D}}{{2 \cdot {\sigma \_{till}}}}$ = $\frac{{1,2 \cdot {{10}^6}Pa \cdot 1,4m}}{{2 \cdot 90 \cdot {{10}^6}Pa}}$ = 9,3 ⋅ 10-3 m
Beregnet godstykkelse blir altså 9,3 mm og beholderen bør derfor lages av 10 mm plater.
Trykkbelastning mot ende-flater i beholdere
Trykk mot ende-flaten i en beholder vil gi langsgående strekkspenninger i beholderveggene.
For å studere dette snitter vi en beholder på tvers av lengderetningen og påfører den avkappede beholderen de krefter som virker på den.
Likevekts betingelsen: (ΣFx = 0), gir oss grunnlag for å finne strekkspenningen.
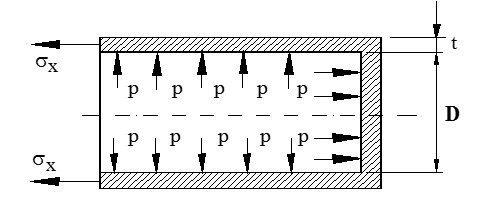
Angrepskraften blir lik trykkresultanten mot ende-flaten:
Fx = p(Pa) ⋅ $\frac{{\pi \cdot {D^2}}}{4}$(m2) (N)
Godsets «forsvars kraft» er lik mobilisert spenning ganger strukket areal.
Strukket areal A = t ⋅ π ⋅ D (m2)
ΣFx = 0 ⇒ Fx = σx ⋅ A = σx ⋅ t ⋅ π ⋅ D $ \Rightarrow $
σx ⋅ t ⋅ π ⋅ D = p ⋅ $\frac{{\pi \cdot {D^2}}}{4}$
Dette gir strekkspenning (σx) :
σx = $\frac{{p \cdot \frac{{\pi \cdot {D^2}}}{4}}}{{\pi \cdot D \cdot t}}$ = $\frac{{p \cdot D}}{{4 \cdot t}}$ (Pa)
Av formelen over ser vi at strekkspenning i beholderens lengderetning er halvparten av hva den var på tvers av beholderen.
Herav følger at dersom trykket blir stort nok, vil sprekker alltid oppstå på langs av rør og beholdere.
1.3.3 Strømning i rør
Bernoullis ligning
Bernoullis ligning uttrykker energiloven for et vilkårlig kontrollvolum (system). Om vi ser bort fra tap, gjelder ifølge energiloven, at det totale energiinnholdet i to punkter på samme strømlinje er konstant.
I figuren under er vist et strømrør med kontrollvolum eller system avgrenset av snittflatene A1 og A2. Vi ser bort fra tap og skriver opp energibalansen for kontrollvolumet:
$\frac{\mathrm{p}_{\mathrm{1}}}{\mathrm{\rho}}$ + $\frac{c_{1}^{2}}{2}$ + g ⋅ h1 = $\frac{\mathrm{p}_{\mathrm{2}}}{\mathrm{\rho}}$ + $\frac{c_{2}^{2}}{2}$ + g ⋅ h2 (J/kg)
Dette er Bernoullis ligning for tapsfri strømning, uttrykt i Joule per kg strømningsmedium.
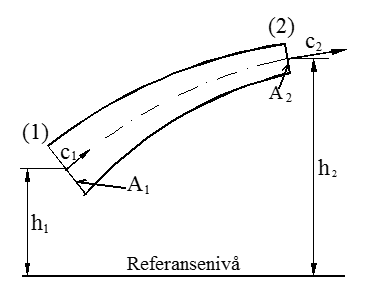
Kontrollvolum (systemgrense)
p1 og p2 = manometertrykk (Pa)
c1 og c 2 = middelhastigheter (m/s)
h1 og h2 = stedshøyder (m)
ρ = tetthet (kg/m3)
g = 9,81 (m/s2)
For væskeberegninger er det praktisk å uttrykke Bernoullis ligning i meter væskesøyle. Omregning fra energienheten J/kg til meter væskesøyle får vi ved å dividere på begge sider av ligningen med tyngdeakselerasjonen (g).
Vi dividerer alle ledd i ligning (1) med (g) og får:
$\frac{\mathrm{p}_{\mathrm{1}}}{\mathrm{\text{ρg}}}$ + $\frac{\mathrm{c}_{\mathrm{1}}^{\mathrm{2}}}{\mathrm{2g}}$ + h1 = $\frac{\mathrm{p}_{\mathrm{2}}}{\mathrm{\text{ρg}}}$ + $\frac{\mathrm{c}_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2g}}$ + h2 (m)
For væskeberegninger velger vi gjerne referansenivået slik at enten h1 eller h2 blir null, og for horisontale rør får vi: h1= h2 = 0.
For trykk velger vi normalt atmosfæretrykket som referansetrykk, dvs. alle trykk lik atmosfære- trykket blir da lik null.
Kontinuitetsligningen
Ved strømning i rørledninger regner vi vanligvis med middelhastigheten i tverrsnittet. Om strømningen er kontinuerlig, må det passere en konstant væskemengde per tidsenhet gjennom ethvert tverrsnitt. Dette uttrykker vi ved kontinuitetsligningen:
Kontinuitetsligningen
qv = A1 ⋅ c1 = A2 ⋅ c2 = A ⋅ c (m3/s)
Her er (qv) volumstrøm i m3/s, (A) er tverrsnitts arealet i m2 og (c) er middelhastigheten i m/s.
Ved å multiplisere med mediets tetthet (ρ) i kg/m3, får vi massestrømmen:
$\dot{\mathrm{m}}$ = qv ⋅ ρ = A ⋅ c ⋅ ρ (kg/s)
Eksempel - Bernoulli og kontinuitetsligningen
Olje strømmer gjennom et horisontalt rør med jevnt økende tverrsnitt, se skisse.
Oppgitt: d1=100 mm, d2 = 150 mm, p1= 126 kPa, p2 = 140 kPa og tetthet (ρ) = 800 kg/m3.
Bestem volumstrømmen i m3/s.
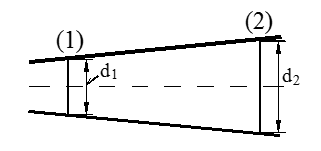
A1 = $\frac{\mathrm{\pi}}{\mathrm{4}}$ ⋅ 0,12 = 7,854 ⋅ 10-3 m2
A2 = $\frac{\mathrm{\pi}}{\mathrm{4}}$ ⋅ 0,152 = 17,7 ⋅ 10-3 m2
Kontinuitetsligningen gir:
$\frac{{{c_1}}}{{{c_2}}}$ = $\frac{{{A_2}}}{{{A_1}}}$ ⇒ c1 = $\frac{{17,7}}{{7,85}}$ ⋅ c2 $ \Rightarrow $ c1 = 2,25 ⋅ c2
$\frac{\mathrm{p}_{\mathrm{1}}}{\mathrm{\text{ρg}}}$ + $\frac{\mathrm{c}_{\mathrm{1}}^{\mathrm{2}}}{\mathrm{2g}}$ + h1 = $\frac{\mathrm{p}_{\mathrm{2}}}{\mathrm{\text{ρg}}}$ + $\frac{\mathrm{c}_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2g}}$ + h2 (m)
$\frac{{126 \cdot {{10}^3}}}{{800 \cdot 9,8}}$ + $\frac{{c_1^2}}{{2 \cdot 9,8}}$ + 0 = $\frac{{140 \cdot {{10}^3}}}{{800 \cdot 9,8}}$ + $\frac{{c_2^2}}{{2 \cdot 9,8}}$ + 0 ⇒
${c_1^2}$ − ${c_2^2}$ = 35 ⇒ (2,25c2)2 − ${c_2^2}$ = 35 ⇒ c2 = 2,94 m/s
Volumstrøm (qv):
qv = A2 ⋅ c2 = 17,7 ⋅ 10-3 (m2) ⋅ 2,94(m/s) = 0,052 m3/s
Strømningstap i rørsystem
Ved strømning i rør og kanaler vil det opptre energitap som følge av friksjon mellom fluid og rørvegger. Ved passering gjennom ventiler og annen armatur tapes det også energi. Slike tap beregner vi ved hjelp av empiriske formler.
Tap i rørsystem inndeles praktisk i rørfriksjonstap og enkeltmotstander.
Rørfriksjonstap
Friksjonstap i rør uttrykkes ved:
hFR = $\frac{\mathrm{}\mathrm{\ \cdot}\mathrm{\ }\mathrm{l\ \cdot \ }\mathrm{c}^{\mathrm{2}}}{\mathrm{2}\mathrm{\ }\mathrm{\cdot}\mathrm{\ }\mathrm{\text{g }}\mathrm{}\mathrm{\ }\mathrm{d}_{\mathrm{h}}}$ (m)
hFR = friksjonstap i meter væskesøyle
λ = rørfriksjonskoeffisient (dimensjons løs)
l = rørlengde (m)
dh = hydraulisk diameter (= diameter for rør) (m)
c = middelhastighet (m/s)
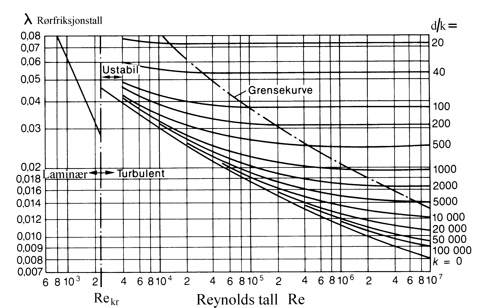
Rørfriksjon (Moodys diagram)
Friksjonskoeffisienten (λ) kan vi beregne ved hjelp av empiriske formler eller ved avlesning i diagram, som for eksempel Moodys diagram for rørfriksjon, se figuren under. I diagrammet er (λ) fremstilt som funksjon av Reynolds tall (Re). Relativ ruhet d/k langs høyre vertikalakse. For stålrør varierer k typisk fra ca. 0,05 til 0,2.
Eksempel - Friksjonstallet
En oljeledning har innvendig diameter 500 mm. I ledningen strømmer det olje med kinematisk viskositet 50 ⋅10-6 (m2/s). Strømningshastigheten er 1,8 m/s, k = 0,05 mm.
Bestem friksjonstallet.
Reynolds tall:
Re = $\frac{\mathrm{c \bullet d}}{\mathrm{\nu}}$ = $\frac{\mathrm{1,8}\frac{\mathrm{m}}{\mathrm{s}}\mathrm{\ \bullet 0,5m}}{\mathrm{50 \bullet 10}^{\mathrm{- 6}}\mathrm{\ }\frac{\mathrm{m}^{\mathrm{2}}}{\mathrm{s}}}$ = 18 ⋅103
$\frac{\mathrm{d}}{\mathrm{k}}$ = $\frac{\mathrm{500mm}}{\mathrm{0,05mm}}$ = 10000
I Moodys diagram avleser vi: λ = ca. 0,027
Enkeltmotstander
Enkeltmotstander i ventiler og bend er bestemt ved:
hte = Σ ζ ⋅ $\frac{\mathrm{c}^{\mathrm{2}}}{\mathrm{2g}}$ (m)
Der ζ (zeta) er en motstandskoeffisient. For overslagsberegninger kan vi bruke følgende verdier:
ζ ≈ 4 - 6 for åpne tallerkenventiler
ζ ≈ 0,5 for 90 grader rørbend
Det samlete tapet er summen av friksjons- og enkelttap:
ht = hFR + hte (m)
Tapene uttrykt i trykkenheter får vi ved å multiplisere med faktoren (ρg)
Δpt (Pa) = ρ(kg/m3) ⋅ g(m/s2) ⋅ ht(m) (Pa)
Bernoullis ligning med tap kan vi nå skrive slik:
$\frac{\mathrm{p}_{\mathrm{1}}}{\mathrm{\text{ρg}}}$ + $\frac{\mathrm{c}_{\mathrm{1}}^{\mathrm{2}}}{\mathrm{2g}}$ + h1 = $\frac{\mathrm{p}_{\mathrm{2}}}{\mathrm{\text{ρg}}}$ + $\frac{\mathrm{c}_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2g}}$ + h2 + ht (m)
Eksempel Tap i rørledninger
Et rør med diameter 200 mm transporterer 70 liter vann pr sekund. Røret består av en rett rørlengde l = 45 m, der friksjons koeffisienten λ = 0,019, fire bend der ζ = 0,35 for hvert, og to ventiler der ζ = 4 for hver. Vannets tetthet ρ = 1000 kg/m3.
Bestem tapene i rørledningen.
Løsning:
Kontinuitetsligningen gir strømningshastigheten:
c = $\frac{\mathrm{q}_{\mathrm{v}}}{\mathrm{A}}$ = $\frac{\mathrm{70 \bullet 10}^{\mathrm{- 3}}\mathrm{\bullet 4}}{\mathrm{\pi \bullet 0,2}^{\mathrm{2}}}$ = 2,2 m/s
Vi velger å beregne tapene uttrykt i trykkenheter.
Trykkfall på grunn av friksjon:
ΔpFR = $\frac{\mathrm{\lambda \bullet \rho \bullet c}^{\mathrm{2}}\mathrm{\bullet l}}{\mathrm{2 \bullet d}}$ = $\frac{\mathrm{0,019 \bullet 1000 \bullet 2,2}^{\mathrm{2}}\mathrm{\bullet 45}}{\mathrm{2 \bullet 0,2}}$ = 10340 Pa
Trykkfall på grunn av enkeltmotstander:
ΔpE = ∑ ζ ⋅ $\frac{\mathrm{c}^{\mathrm{2}}\mathrm{\bullet \rho}}{\mathrm{2}}$ = (0,35 + 4 ⋅ 2) $\frac{\mathrm{2,2}^{\mathrm{2}}\mathrm{\bullet 1000}}{\mathrm{2}}$ = 19360 Pa
Det totale trykktapet er summen av alle tap:
Δptap= 10340 Pa + 19360 kPa = 29700 Pa
Beregnet trykktap kan omregnes til meter væskesøyle ved å dividere med faktoren (ρg).
Dette gir totalt tap i m:
htap = $\frac{\mathrm{p}}{\mathrm{\rho \bullet g}}$ = $\frac{\mathrm{29700}}{\mathrm{1000 \bullet 9,8}}$ = 3,0 m (= væskesøylehøyde)
1.3.4 Strømning i dyser
Figuren under viser en konvergerende dyse skjematisk, og et hs-diagram for strømningen gjennom dysen.
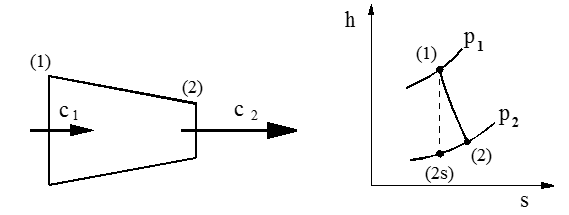
For strømningsprosesser gjelder energiligningen:
h1 − h2 = ($\ \frac{1}{2}c_{1}^{2}$ – $\ \frac{1}{2}c_{2}^{2}\ )$ ⋅ 10−3 (kJ/kg)
Ved strømning i dyser er innløpshastigheten (c1) som regel, så liten at vi kan sløyfe den. Ved å innføre c1 = 0, får vi utløpshastigheten (c2):
c2 = $\sqrt{\mathrm{2}\left( \mathrm{h}_{\mathrm{1}} - \mathrm{\ }\mathrm{h}_{\mathrm{2}} \right)\mathrm{\bullet \ }\mathrm{10}^{\mathrm{3}}}$ (m/s)
h1 − h2 = entalpiendring (kJ/kg)
Om vi antar at strømningen i dysen er isentropisk, kan det vises at vi oppnår maksimal utløpshastighet når mottrykket (p2) er null. Maksimal (teoretisk) hastighet blir da:
cmaks = $\sqrt{\mathrm{2}\frac{\mathrm{\kappa}}{\mathrm{\kappa\ - \ 1}}\mathrm{R}\mathrm{T}_{\mathrm{1}}}$ (m/s)
κ = isentropeksponent for mediet
Eksempel - Maksimal teoretisk utløpshastighet:
For vanndamp er gitt: Innløpstemperatur t1 = 400°C, gasskonstanten R = 460 J/kgK, κ = 1,3.
Bestem maksimal utløpshastighet.
Ligningen over gir maksimal utløpshastighet (cmaks):
cmaks = $\sqrt{\mathrm{2}\frac{\mathrm{1,3}}{\mathrm{1,3\ - \ 1}}\mathrm{\ 460\ }\mathrm{}\mathrm{\ 673}}$ (m/s) = 1638 m/s
Merk at den teoretiske hastigheten har liten praktisk interesse, da de fleste gasser vil kondensere eller sublimere lenge før vi når trykket (p2) = 0.
Kritisk hastighet (lydhastighet)
Når mottrykket når en bestemt verdi, det såkalte kritiske trykk, stopper ekspansjonen opp i vanlige dyser og ved lekkasjer. Dette kritiske trykkforholdet (pk/p1) er et karakteristisk forholdstall for alle (ideelle) gasser, definert som følger:
Kritisk trykkforhold: pk/p1 = $\left( \frac{\mathrm{2}}{\mathrm{\kappa\ - 1}} \right)^{\frac{\mathrm{\kappa}}{\mathrm{\kappa\ - 1}}}$
For (p2/p1)$ \le $ (pk/p1) stopper ekspansjonen når trykket p2 = pk og hastigheten er da lik kritisk hastighet ck:
ck = $\sqrt{\mathrm{2}\frac{\mathrm{\kappa}}{\mathrm{\kappa\ - \ 1}}\mathrm{R}\mathrm{T}_{\mathrm{1}}}$ (m (m/s)
Den kritiske hastigheten (ck) er lik lydhastigheten i gassen.
Eksempel – Damphastighet i dyse
Mettet damp av 10 bar skal ekspandere i en dyse til p2 = 6 bar og massestrømmen er 1 kg/s.
Bestem teoretisk hastighet og utløpsarealet. For mettet damp er κ = 1,3.
Kritisk trykkforhold:
$\frac{\mathrm{p_k}{}}{\mathrm{p_1}}$=$\left( \frac{\mathrm{2}}{\mathrm{\kappa\ - 1}} \right)^{\frac{\mathrm{\kappa}}{\mathrm{\kappa\ - 1}}}$ = $\left( \frac{\mathrm{2}}{\mathrm{1,3\ - 1}} \right)^{\frac{\mathrm{1,3}}{\mathrm{1,3\ - 1}}}$ = 0,577
Virkelig trykkforhold:
$\frac{\mathrm{p2}{}}{\mathrm{p}}$ = $\frac{6}{10}$ = 0,6
Trykkforholdet p2/p1 = 0,6 er altså større enn det kritiske. I dette tilfellet slutter derfor ekspansjonen før det kritiske trykket og kritisk hastighet er nådd. Teoretisk hastighet er da bestemt av:
c2 = = $\sqrt{\mathrm{2}\left( \mathrm{h}_{\mathrm{1}} - \mathrm{\ }\mathrm{h}_{\mathrm{2}} \right)\mathrm{\bullet \ }\mathrm{10}^{\mathrm{3}}}$ = = $\sqrt{\mathrm{2}\left( 2780 - 2680\mathrm{\ } \right)\mathrm{\bullet \ }\mathrm{10}^{\mathrm{3}}}$ = 440 m/s
Fra Mollier-diagram: v2 = 0,305 m3/kg $ \Rightarrow $ ρ = $\frac{1}{{0,305}}$ = 3,279 kg/m3
Av kontinuitetsligningen får vi utløpsarealet (A2):
A2 = $\frac{\dot{\mathrm{m}}}{\mathrm{ρ\ \cdot\ }\mathrm{c}_{\mathrm{2}}}$ = $\frac{\mathrm{1}}{\mathrm{3,279\ \bullet \ 440}}$ = 6,9 ⋅10-4 m2
Lavaldysen
Maksimal hastighet i vanlige dyser er som nevnt, begrenset til lydhastigheten. Dette innebærer at dersom mottrykket er lavere enn det kritiske trykket, vil ekspansjonen likevel stanse ved det kritiske trykket. Figuren under illustrerer dette, når trykket er sunket til (pk) vil videre ekspansjon gå med til virveltap og støy mv.
Lavaldysen er utformet slik at gassen, ved bestemte mottrykk, kan ekspandere helt ned til det aktuelle mottrykket. Utløpshastigheten vil da kunne øke utover den kritiske hastigheten.
Dette er illustrert i figuren under.
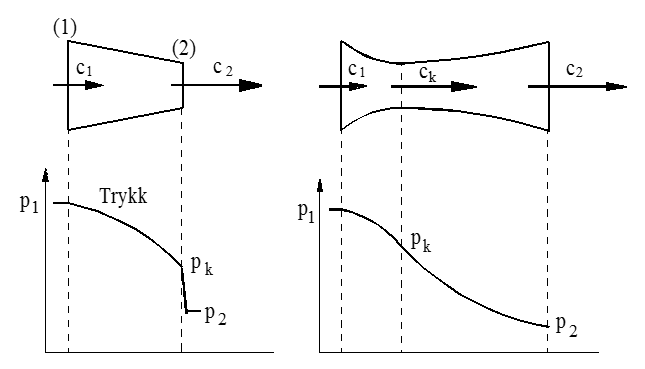
Konvergerende dyse Lavaldyse
Teoretisk utløpshastigheten fra en Lavaldyse er bestemt ved:
c2 = $\sqrt{\mathrm{2}\left( \mathrm{h}_{\mathrm{1}} - \mathrm{\ }\mathrm{h}_{\mathrm{2}} \right)\mathrm{\bullet \ }\mathrm{10}^{\mathrm{3}}}$ (m/s)
Utløpshastigheten fra en lavaldyse kan som nevnt, være større enn lydhastigheten, men massestrømmen gjennom Lavaldysen er likevel begrenset av kritisk hastighet, som opptrer i det minste tverrsnittet.
Merk at ved bestemte trykkforhold kan det oppstå såkalte kompresjonsstøt i dysen, som medfører at hastigheten plutselig skifter fra supersonisk til subsonisk. Strømningsforholdene blir da vesentlig mer komplekse og blir ikke behandlet her.
Slike kompresjonsstøt forekommer for eksempel i forbindelse med overlydsfly og er årsak til de ekstremt høye "lydsmell" som oppstår når overlydsfly passerer i vår nærhet.
Eksempel – Damphastighet i Lavaldyse
Tørrmettet damp av 10 bar skal ekspandere til 1 bar mottrykk i en dyse. Massestrøm gjennom dysen er 1 kg/s.
Bestem de teoretiske hastigheter.
Løsning:
Vi bestemmer trykkforholdet:
$\frac{\mathrm{p}_{\mathrm{2}}}{\mathrm{p}_{\mathrm{1}}\ }$ = $\frac{1}{10}$ = 0,1
For tørrmettet damp (κ = 1,3) får vi kritisk trykkforhold:
$\frac{\mathrm{p}_{\mathrm{k}}}{\mathrm{p}_{\mathrm{1}}\ }$ = $\left( \frac{\mathrm{2}}{\mathrm{\kappa\ - 1}} \right)^{\frac{\mathrm{\kappa}}{\mathrm{\kappa\ - 1}}}$ = $\left( \frac{\mathrm{2}}{\mathrm{1,3\ - 1}} \right)^{\frac{\mathrm{1,3}}{\mathrm{1,3\ - 1}}}$ = 0,577
Trykkforholdet er her lik 0,1 som altså er mindre enn det kritiske trykkforholdet på 0,577 og dysen må derfor utformes som en Lavaldyse, idet vanlige dyser kun kan ekspandere til kritisk trykk, dvs. i dette tilfellet til 5,77 bar.
Dysens minste tverrsnitt er bestemt av kritisk trykkforhold og kritisk hastighet, dvs. ved en tenkt ekspansjon fra begynnelsestrykket p1 = 10 bar, til kritisk trykk pk = 5,77 bar.
ck = $\sqrt{\mathrm{2}\left( \mathrm{h}_{\mathrm{1}} - \mathrm{\ }\mathrm{h}_{\mathrm{k}} \right)\mathrm{\bullet \ }\mathrm{10}^{\mathrm{3}}}$ (m/s)
Innsatt verdier (fra Mollier diagram) gir:
ck = = 450 m/s
ck = hastighet i minste tverrsnitt
Utløpshastighet (c2) i Lavaldysen er bestemt ved «hele» entalpifallet, dvs. vi får:
c2 = $\sqrt{\mathrm{2}\left( \mathrm{h}_{\mathrm{1}} - \mathrm{\ }\mathrm{h}_{\mathrm{2}} \right)\mathrm{\cdot \ }\mathrm{10}^{\mathrm{3}}}$ (m/s)
Innsatt verdier fra Mollier-diagram gir utløpshastigheten (c2):
c2 = $\sqrt{\mathrm{2}\left( 2780 - 2390\mathrm{\ } \right)\mathrm{\cdot \ }\mathrm{10}^{\mathrm{3}}}$ = 880 m/s
1.3.5 Pumpesystem
Leveringshøyde H
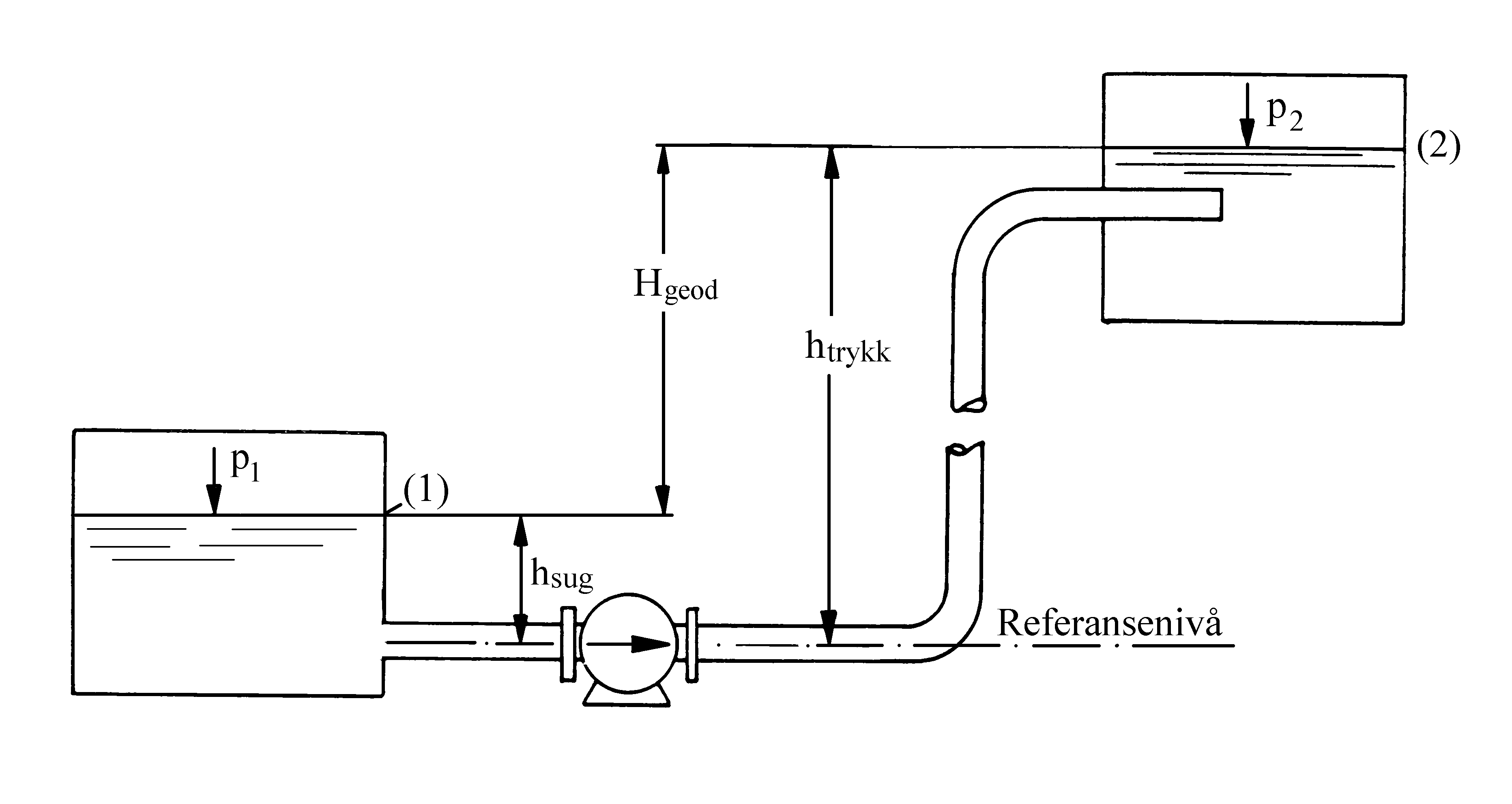
En pumpe transporterer væsker ved at energi (arbeid) overføres til pumpemediet. Ofte er pumpens oppgave å transportere væsker fra et lavere til et høyere nivå, derved øker væskens stillingsenergi. I andre tilfeller er oppgaven å trykke en væske inn i en tank eller beholder med høyere trykk enn omgivelsene, da øker væskens trykkenergi etc. Figuren under viser et pumpesystem der væske blir pumpet fra en tank til en annen.
Pumpesystem
Nødvendig pumpeenergi for en bestemt transportoppgave beregner vi enklest på grunnlag av Bernoullis ligning. Vi har da følgende sammenheng:
H = Hgeod + $\frac{\mathrm{p}_{\mathrm{1}}\mathrm{}\mathrm{\ }\mathrm{p}_{\mathrm{2}}}{\mathrm{\text{ρ g}}}$ + $\frac{\mathrm{c}_{\mathrm{1}}^{\mathrm{2}}\mathrm{\ }\mathrm{}\mathrm{\ }\mathrm{c}_{\mathrm{2}}^{\mathrm{2}}}{\mathrm{2}}$ + htap (m)
H = leveringshøyde = pumpeenergi uttrykt i meter væskesøyle
Hgeod = htrykk − hsug = geodetisk (statisk) høydeforskjell (m)
p1,p2 = væsketrykk inn/ut (av kontrollvolumet) (Pa)
c1, c2 = væskehastighet inn/ut (av kontrollvolumet) (m/s)
ρ = væskens tetthet (kg/m3)
htap = summen av alle tap (i kontrollvolumet) (m)
For systemet vist i figuren over er c1 og c2 lik væskeoverflatenes hastighet, som i praksis er liten i forhold til rørhastigheten. Vi kan derfor sette c1 = c2 = 0. Vi får da:
H = Hgeod + $\frac{{\mathop p\nolimits_1 - \mathop p\nolimits_2 }}{{\rho g}}$ + htap (m)
Eksempel - Pumpesystem
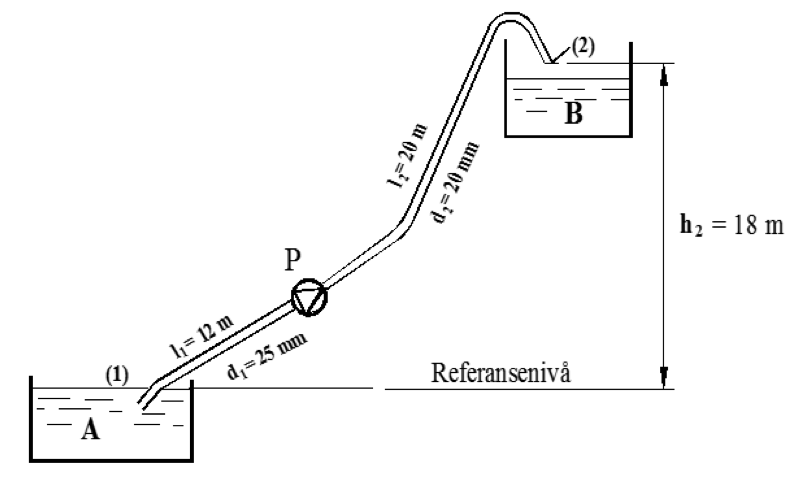
Pumpen P skal pumpe qv = 4 dm3 vann pr sekund fra beholder A og opp i beholder B. Rørledningen har mål som vist på figuren og består av et sugerør (1) og et trykkrør (2). Vi skal beregne hvor stor effekt pumpen må yte.
Pumpesystem
Vannet som starter i kar A, vil tape energihøyde etter hvert som det beveger seg oppover sugerøret. Men når det passerer pumpen, vil det motta energi fra pumpen og energihøyden øker da med en verdi tilsvarende pumpetrykket.
Økningen i energihøyde må være stor nok til at vannet kan fortsette gjennom trykkrøret til utløpsåpningen over kar B.
Pumpeeffekten er bestemt av:
Pp = $\frac{{\rho \cdot g \cdot {q_v} \cdot H}}{{{\eta _p}}}$ (W)
ρ = væskens tetthet (kg/m3)
qv = volumstrøm gjennom pumpen (m3/s)
H = total energihøyde (leveringshøyde) (m)
ηp = pumpens virkningsgrad
For å beregne effekten må vi altså beregne leveringshøyden H.
Vi måler stedshøyder i forhold til et horisontalplan langs vannspeilet i kar A, og kaller dette snitt (1). Vannet i karet har da energihøyde h1 = 0. Trykket ved innløp (1) og utløp (2) er lik atmosfæretrykket, dvs. trykkhøydene er null. Det nødvendige pumpetrykk for at vannet skal strømme som forutsatt blir:
H = h2 + $\frac{{c_2^2}}{{2g}}$ + htap (m)
Her er htap lik summen av alle tap mellom karet A og utløpsåpningen (2). Vi bestemmer vannhastighetene:
Hastighet i trykkledningen:
c2 = $\frac{\mathrm{q_v(m^3/s)}}{\mathrm{\frac{{\pi}\cdot{d_2^2}}{4}}}$ = $\frac{{4 \cdot {{10}^{ - 3}}}}{{\frac{{\pi \cdot {{0,2}^2}}}{4}}}{}$ = 1,28 m/s
Hastighet i sugerøret:
c1 = c2 ⋅ $\mathrm {\left( {\frac{{{d_2}}}{{{d_1}}}} \right)^2}$= 1,28 ⋅ ${\left( {\frac{{{20}}}{{{25}}}} \right)^2}$ = 0,82 m/s
Av enkeltmotstander i rørledningen skal vi her bare ta med motstanden fra en sil, som vi forutsetter er plassert foran innløpet til sugerøret. Tapskoeffisienten settes til 2. For rørfriksjonen regner vi med λ = 0,03 og pumpevirkningsgraden settes til 0,8.
Tap i sugerøret: ζ ⋅ $\frac{{c_1^2}}{{2g}}$ + $\frac{{\lambda \cdot c_1^2 \cdot {l_1}}}{{2 \cdot g \cdot d}}$ = 2 ⋅$\frac{{{{0,82}^2}}}{{2 \cdot 9,81}}$ + $\frac{{0,03 \cdot {{0,82}^2} \cdot 12}}{{2 \cdot 9,81 \cdot 0,025}}$ = 0,56 m
Tap i trykkrøret: $\frac{{\lambda \cdot c_2^2 \cdot {l_2}}}{{2 \cdot g \cdot {d_2}}}$ = $\frac{{0,03 \cdot {{1,28}^2} \cdot 20}}{{2 \cdot 9,81 \cdot 0,020}}$ = 2,5 m
Samlet tap i rørledningen: ht = 0,56 + 2,5 = 3,06 m
Dette gir leveringshøyden: H = 18 m + $\frac{{{{1,28}^2}}}{{2 \cdot 9,81}}$ + 3,06 = 21,1 m
Vi kan nå beregne pumpeeffekten:
Pp = $\frac{{\rho \cdot g \cdot {q_v} \cdot H}}{{{\eta _p}}}$ = $\frac{{1000 \cdot 9,81 \cdot 4 \cdot {{10}^{ - 3}} \cdot 21,1}}{{0,8}}$ = 1035 W = 1,035 kW
Sugehøyde og kavitasjon
Leveringshøyden H kan inndeles i suge- og trykkhøyde:
H = Hsug + Htrykk
Sugehøyden Hsug er da lik summen av statisk sugehøyde (hsug), motstandstap i sugeledning og trykkforskjell fra atmosfæretrykket. Figurene under viser to vanlige arrangement på sugesiden i et pumpesystem.
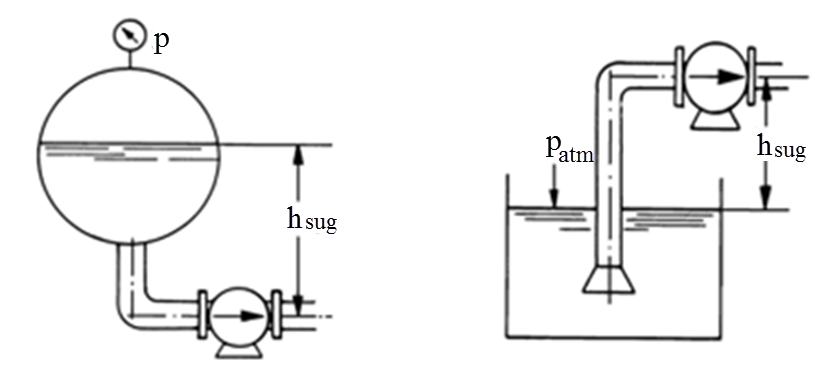
Dersom trykket på sugesiden av en pumpe blir lavere enn væskens damptrykk, oppstår det såkalt kavitasjon. Det dannes da luftbobler som vil implodere når trykket igjen øker. Dette medfører uheldige trykksvingninger og mekaniske belastninger på gods mm, som i verste fall kan skade pumpe og ventiler i systemet.
Det laveste trykket i et pumpesystem opptrer på sugesiden av pumpen. Figuren under viser suge siden av et pumpesystem. Vi anvender Bernoullis ligning for systemet og får:
ps = p1 − (hs ⋅ ρ ⋅ g + htap ⋅ ρ ⋅ g + $\frac{{\rho \cdot c_s^2}}{2}$) (Pa)
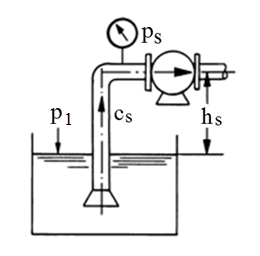
ps = trykk på sugeside av pumpen (Pa)
p1 = trykk over væskeflaten (Pa)
hs = statisk sugehøyde (m)
htap = sum tap på sugeside (m)
cs = hastighet på sugesiden (m/s)
(c1 = væskeflatens hastighet er sløyfet)
Dersom sugetrykket (ps) blir mindre eller lik væskens damptrykk (pD) ved en gitt temperatur, oppstår det kavitasjon.
NPSH
Vi er kjent med at atmosfæretrykket er ca. 1 bar (100 kPa). Dette tilsvarer ca. 10 meter vannsøyle og utgjør den «hjelpen» en pumpe har til å suge opp væske. Imidlertid er det flere faktorer som spiller inn og motvirker denne hjelpen. En av disse faktorene er væskens damptrykk (pD) som øker sterkt med temperaturen, se tabell.
Omtrentlige damptrykk for vann
| Temperatur (oC) | 10 | 20 | 30 | 40 | 50 | 70 |
| Damptrykk (m Vs) | ≈ 0 | ≈ 0 | 0,5 | 0,8 | 1,3 | 3,2 |
For vanlig kaldt vann er altså damptrykket neglisjerbart, mens det for vann ved 100°C er økt til atmosfæretrykket. Vann ved 100°C kan derfor ikke suges fra en åpen tank.
Grensetrykket for kavitasjon angis ofte som NPSH (Net Positive Suction Head). Vi skiller mellom nødvendig og tilgjengelig
Nødvendig NPSHNV (også kalt holdetrykk) har med pumpens konstruksjon å gjøre og representerer den minimale nødvendige margin mellom totaltrykket på sugesiden (Hsug) og damptrykket ved en gitt kapasitet:
Nødvendig NPSHNV kan defineres ved:
NPSHNV = Hsug − $\frac{{\mathop p\nolimits_D }}{{\rho \cdot g}}$ (m)
NPSHNV oppgis av pumpefabrikanten.
Tilgjengelig NPSHTG har med systemet der pumpen arbeider å gjøre og er lik differansen mellom trykket på sugesiden av pumpen og damptrykket ved den aktuelle temperaturen.
Tilgengelig NPSH kan defineres ved:
NPSHTG = $\frac{{\mathop p\nolimits_1 }}{{\rho \cdot g}} - \frac{{\mathop p\nolimits_s }}{{\rho \cdot g}} - \mathop h\nolimits_{tap} - \frac{{\mathop p\nolimits_D }}{{\rho \cdot g}}$ (m)
p1 = trykk over væskeflate (sugeside) (Pa)
ps = sugetrykk v/innløp pumpe (Pa)
pD = væskens damptrykk (Pa)
ρ = væskens tetthet (kg/m3)
htap = sum tap på sugeside (m)
Eksempel - kavitasjonskontroll
Fra datablad for en neddykket brann saltvannspumpe har vi følgende:
Saltvannstemperatur = 6 - 11 °C
Tetthet ρ = 1026 kg/m3
Damptrykk pD = 0,013 bar (overtrykk)
Sugetrykk ved pumpen ps = 1,27 bar (overtrykk)
Leveringshøyde H = 176,3 m
Kapasitet qv = 740 m3/h
NPSH - nødvendig = 3 m
NPSH - nødvendig v/150 % kapasitet = 4,5 m
Vi skal kontrollere om det er fare for kavitasjon i pumpen.
Beregner tilgjengelig NPSH:
NPSHTG = $\frac{{\mathop p\nolimits_s }}{{\rho \cdot g}} - \frac{{\mathop p\nolimits_D }}{{\rho \cdot g}}$
NPSHTG = $\frac{\mathrm{(1,27 – 0,013)\cdot{10^5}(Pa)}}{\mathrm{1026(m^3/kg)\cdot{9,81(m/s^2)}}}$ = 12,5 m
Vi ser at det er god margin med hensyn til kavitasjon.
Kavitasjonskontroll for ekstreme forhold:
Vi antar at pumpen må kjøres med 150 % kapasitet, dvs. NPSH nødvendig er 4,5 m. Videre antas at det har oppstått et oljeutslipp og at pumpen begynner å suge olje.
Data for oljen er: pD = 0,6 bar, ρ = 860 kg/m3
NPSHTG = $\frac{\mathrm{(1,27 – 0,6)\cdot{10^5}(Pa)}}{\mathrm{860(kg/m^3)\cdot{9,81}(m/s^2)}}$ = 7,9 m
Også i dette tilfelle er NPSH tilgjengelig > NPSH nødvendig.
Systemkurver og pumperegulering
Av det foregående følger at friksjonsmotstand og enkeltmotstander øker (tilnærmet) proporsjonalt med kvadratet av hastigheten. Totalmotstanden eller leveringshøyden (H) kan derfor uttrykkes ved:
H = konstant ⋅ $q_v^2$
qv = volumstrøm (m3/s)
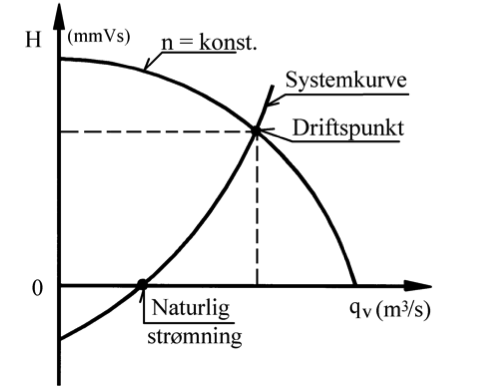
Herav følger at leveringshøyden (H) i prinsippet er proporsjonal med annen potens av volumstrømmen.
I figuren til høyre er vist en typisk systemkurve for kjølevannssystem på skip. I figuren er også inntegnet en turtallskurve (pumpekurve) for en sentrifugalpumpe.
Systemets driftspunkt er skjæringspunktet mellom pumpens turtallskurve og system- kurven.
Pumperegulering
Ved konstant omdreiningstall vil en stempelpumpe levere tilnærmet konstant væskemengde, uansett leveringstrykk. For sentrifugalpumpen vil derimot væskemengden øke når leverings- trykket reduseres. Slike data oppgis gjerne av fabrikanten i form av en pumpekurve, der løftehøyden (H) er gitt som funksjon av volumstrømmen i f.eks. m3/min, m3/s eller m3/h.
Struperegulering
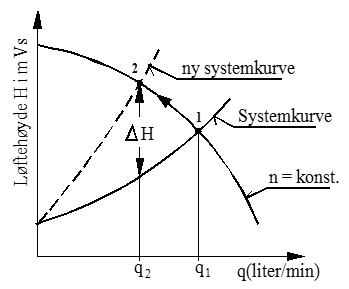
Ved struperegulering innføres et ekstra trykktap (ΔH) i systemet og dermed får vi en "ny" systemkurve.
I figuren til venstre er prinsippet for struperegulering vist, driftspunktet flyttes fra (1) til (2) langs turtallskurven.
Strupetapet ΔH må tilpasses slik at skjæring mellom ny systemkurve og pumpekurven er lik ønsket leveringsmengde.
Struping medfører et unyttig energitap, idet pumpen må yte omtrent samme effekt uansett leveringsmengde.
Retur - regulering
Ved denne reguleringsformen ledes en del av væskestrømmen forbi hele eller deler av systemet i en egen tilbake-ledningsgren. På denne måten reduseres trykktapet i systemet og væskemengden gjennom systemet reduseres, se figur.
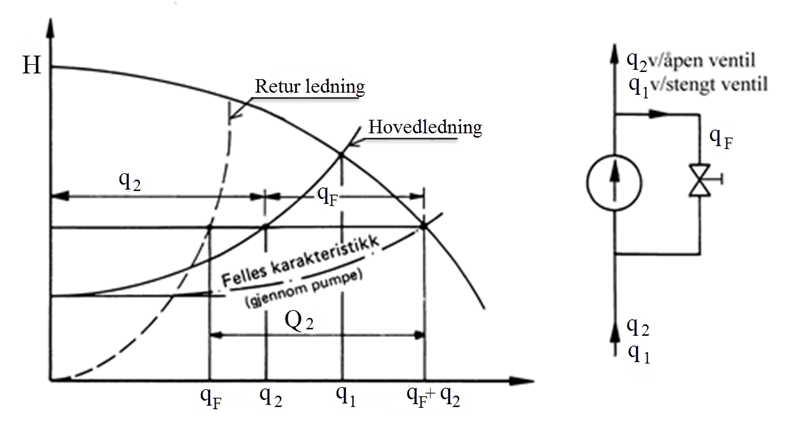
Ved å åpne retur-ventilen flyttes driftspunktet langs systemkurven som vist i figuren. Denne reguleringsformen gir også et "unyttig" energitap ved struping i returledningen.
Turtallsregulering
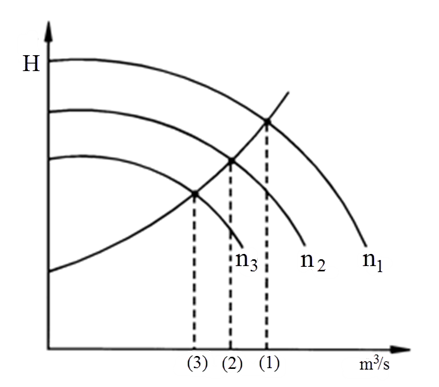
Turtallsregulering
Ved å endre pumpeturtallet, endrer vi også pumpekurven.
I figuren til høyre er vist pumpekurver for tre ulike turtall, der (1) tilsvarer full leveringsmengde mens (2) og (3) tilsvarer leveringsmengden ved lavere turtall.
Energitapet er lite for denne regulerings- formen og vesentlig mindre enn for strupe- og retur-regulering.

