1.2 Mekanikk
1.2.1 Kraft og bevegelse
Sammenhengen mellom kraft og bevegelse bygger på Newtons bevegelseslover:
Newtons 1. lov (Treghetsloven):
Et legeme er i ro eller beveger seg med konstant hastighet langs en rett linje når summen av de ytre kreftene på legemet er lik null.
Newtons 2. lov (Kraftloven)
Når et legeme med masse m blir påvirket av en kraft F, får legemet en akselerasjon a som er proporsjonal med kraften og omvendt proporsjonal med legemets masse.
Newtons 2. lov: F = m ⋅ a (N)
F = resultantkraft (N = kgm/s2)
m = masse (kg)
a = akselerasjon (m/s2)
Merk
Vi uttaler loven slik: Kraft er lik masse ganger akselerasjon.
Stempelbevegelse
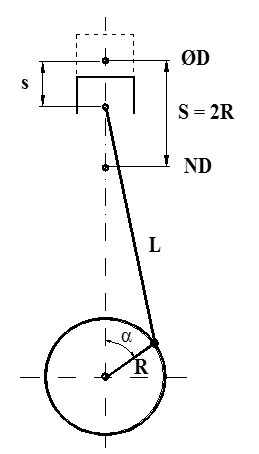
Stempel veiv-system, skjematisk.
For stempelbevegelsen gjelder følgende:
Stempelveien (s):
s = R ⋅ (1 – cos α + $\frac{\lambda }{2}$sin2α) (m)
Stempelhastighet (c):
c = Rω (sin α + $\frac{\lambda }{2}$sin 2α) (m/s)
Stempelakselerasjon (a):
a = Rω2 (cos α + λ ⋅ cos 2α) (m/s2)
s = stempelvei (regnet fra ØD) (m)
R = veivradius (m)
α = veivvinkel (regnet fra ØD)
ω = 2πn = vinkelhastighet (s-1)
L = veivstangslengde (m)
λ = $\frac{R}{L}$= veivstangs-forholdet
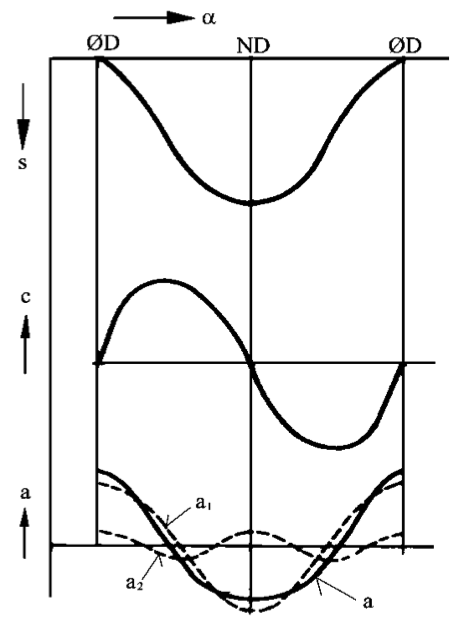 stempelbevegelsen
stempelbevegelsen
Figuren over viser stempelbevegelsen for en hel omdreining av veivakselen.
Merk at akselerasjonen har sitt maksimum når stempelet passerer ØD og ND, mens hastigheten er null i ØD og ND.
På nederste figur er akselerasjonen (a) vist som hel-trukket linje. Men (a) kan også uttrykkes som summen av to ledd, kalt første og andre ordens akselerasjon:
a1 = R ⋅ ω2 ⋅ cos α (1. orden)
a2 = R ⋅ ω2 ⋅ λ ⋅ cos 2 α (2. orden)
På figuren er a1 og a2 vist stiplet.
Stempelets hastighet og akselerasjon varierer altså i perioder på 360° (2π rad.).
Eksempel - stempelbevegelse
En 2-takts motor har slaglengde S = 420 mm, veivstangslengde L = 900 mm og rotasjons-frekvens n = 5,83 s-1. Bestem stempelhastigheten ved α = 30°, 60°, 82° og 138° og stempel- akselerasjonen ved α = 0°, 60°, 82° og 138°.
R = $\frac{S}{2}$ = $\frac{{0,42}}{2}$ = 0,21 m λ = $\frac{R}{L}$ = $\frac{{0,21}}{{0,9}}$ = 0,23 ω = 2π ⋅ 5,83 = 36,6 s−1
Stempelhastighet: c = Rω (sin α + $\frac{\lambda }{2}$sin 2 α)
30° : c = 0,21 ⋅ 36,6 ⋅ (sin 30° + 0,115 ⋅ sin 60°) = 4,6 m/s
60° : c = 0,21 ⋅ 36,6 ⋅ (sin 60° + 0,115 ⋅ sin 120°) = 7,4 m/s
82° : c = 0,21 ⋅ 36,6 ⋅ (sin 82° + 0,115 ⋅ sin 164°) = 7,8 m/s
138° : c = 0,21 ⋅ 36,6 ⋅ (sin138° + 0,115 ⋅ sin 276°) = 4,2 m/s
Akselerasjon: a = Rω2 (cos α + λcos 2 α)
0° : a = 0,21 ⋅ 36,62 ⋅ (1 + 0,23) = + 346 m/s2
60°: a = 0,21 ⋅ 36,62 ⋅ (cos 60° + 0,23 ⋅ cos 120°) = + 108 m/s2
82°: a = 0,21 ⋅ 36,62 ⋅ (cos 82° + 0,23 ⋅ cos 164°) = − 23 m/s2
138°: a = 0,21 ⋅ 36,62 ⋅ (cos 138° + 0,23 ⋅ cos 276°) = − 202 m/s2
1.2.2 Friksjon
Når et legeme glir mot et annet, opptrer det alltid i berøringsflaten en motstand mot bevegelsen, som vi kaller friksjon. Den er ikke begrenset til bevegelse mellom faste legemer eller mellom faste legemer og væsker, men opptrer også der væske- eller gass-lag med forskjellig hastighet berører hverandre, såkalt indre friksjon. Også ved formforandring av faste legemer opptrer det energi-forbrukende krefter som virker som indre friksjon.
Læremål
- Glidefriksjon (statisk og dynamisk).
- Rullemotstand (også kalt rullefriksjon).
- Hydrodynamisk- eller væskefriksjon.
Glidefriksjon
Hvis vi skal trekke et legeme langs en flate trengs det en kraft F som er større enn friksjons- kraften mellom legemet og underlaget, se figuren under. Øker vi kraften F gradvis, vil vi finne at kraften F må være noe større for å få bevegelsen i gang enn for å holde den ved like. Vi snakker om statisk friksjon og dynamisk- eller glidefriksjon.
Friksjonskraften er alltid rettet mot bevegelses- retningen og blir uttrykt ved:
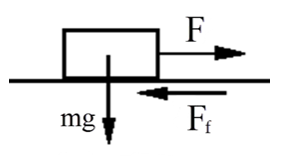
Ff = µ ⋅ FN (N)
Ff = friksjonskraften (N)
FN = mg = normalkraft mot underlaget (N)
µ = friksjonskoeffisient
Forsøk har vist at friksjonskoeffisienten (µ) er tilnærmet uavhengig av berøringsflatenes areal og av normalkraftens størrelse. Tallverdier for (µ) finner vi i ulike håndbøker. Tabellen under viser noen eksempel.
| Materiale | Statisk friksjon | Dynamisk friksjon |
|---|---|---|
| Glass mot glass | 0,9 | 0,4 |
| Stål mot is | 0,03 | 0,02 |
| Stål mot bronse | 0,18 | 0,16 |
| Gummi mot is | 0,03 | 0,02 |
Av tabellen fremgår at glatte flater som glass gir høy friksjonskoeffisient. Ved svært glatte flater, for eksempel høypolerte metaller uten oksidbelegg, kan friksjonen teoretisk bli større enn normalkraften. Grunnen til dette er i korthet at flere molekyler kommer nær hverandre slik at det oppstår tiltrekningskrefter, såkalte adhesjonskrefter, mellom dem.
Lagre og grensesmøring
I lagre gjelder det å ha minst mulig friksjon. Dette kan vi i prinsippet oppnå på to måter, ved smøremidler, og ved kule- eller rullelager. Smøremidler er væsker, særlig oljer, som danner et sammenhengende lag mellom de to flatene. Det blir da bare indre friksjon i smøremidlet som kommer i betraktning, dvs. vi har såkalt hydrodynamisk friksjon.
Gode smøremidler må ha en bestemt molekylform, slik at molekylene lett glir forbi hverandre.
Smøremidlets viskositet må dessuten tilpasses trykk og temperatur mv.
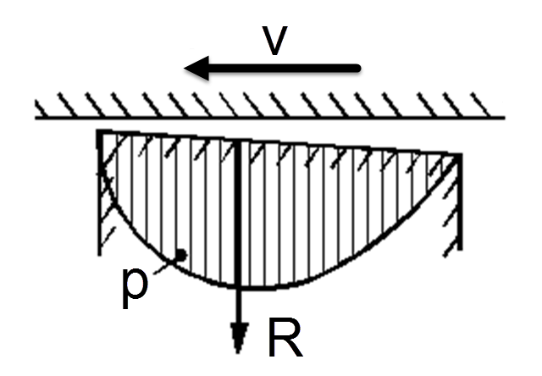
En viktig betingelse for at det skal holde seg en bærende oljefilm mellom to glideflater, er at flatene danner en «liten» vinkel med hverandre, som vist (overdrevet) på figuren til høyre.
Et legeme beveger seg med hastighet (v) i pilens retning. Mellom legemet og det stillestående underlaget får vi et varierende trykk (p) i oljen, som antydet på figuren.
Trykkresultanten R er som regel litt forskjøvet fra midten til nærmere spissen av olje-kilen.
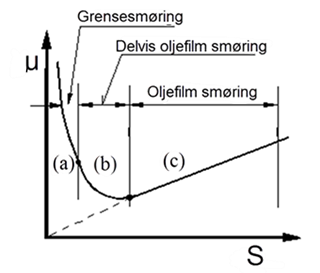
Figuren over viser hvordan friksjons- koeffisienten (µ) varierer som funksjon av Sommerfelds tall[^4] (S):
S = $\frac{\mathrm{\text{υ ⋅ n}}}{\mathrm{p}}\ \left( \frac{d}{C} \right)^{2}$
ν = oljens viskositet
n = rotasjonsfrekvens
p = spesifikk lagerbelastning
C = lagerklaring
I område (c) er smøreoljefilmen sammenhengende. Friksjonen øker da proporsjonalt med S, dvs. med økende viskositet og rotasjonsfrekvens. Slike forhold har vi på smurte lager-flater i en motor.
For parameterverdier i område (a) øker friksjonen sterkt. Oljefilmen er da borte og direkte kontakt mellom flatene hindres bare av overflateaktive molekyler i oljen.
Ved dette kritiske belastningstallet inntrer en sterk økning av friksjonskoeffisienten. En liten økning i belastningen gir en stor økning av (µ). I dette grenseområdet er lagerets sikkerhet mot rivning helt avhengig av smøreoljens kvalitet og egenskaper.
Grensesmøreprosessen ved høye spesifikke belastninger er en labil tilstand. Små endringer i driftstilstanden, skeivheter, slitasje og dårlig smøreolje, kan føre til temperaturøkning i lagerflaten som resulterer i nedsatt fasthet av metallet eller varmgang og i verste fall havari.
1.2.3 Spenninger i aksler og gods
Vridning av aksler
En konstruksjonsdel som blir påvirket av et vridningsmoment, blir vridd. I et vilkårlig snitt normalt på konstruksjonsdelen vil det da bli mobilisert indre krefter i materialet som søker å utbalansere vridningsmomentet.
For en sirkulær homogen aksel vil de mobiliserte vridningsspenningene ha sin største verdi langs periferien og avta lineært til null i senter av akselen, se figur.
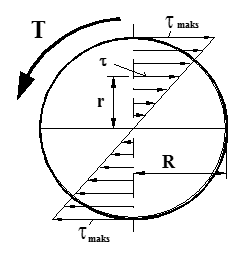
Sammenhengen mellom vridningsmoment og maksimal vridningsspenning kan vi derfor uttrykke slik:
τmaks = $\frac{T}{{{W_p}}}$
T = vridningsmoment (Nm)
Wp = $\frac{\mathrm{\text{πD}}^{\mathrm{3}}}{\mathrm{16}}$ = polart motstandsmomentet (m3)
τmaks = maksimal vridningsspenning (N/m2)
Vridningsvinkel
Hvis en aksel med lengde (l) blir utsatt for et vridningsmoment (T), vil den vri seg en viss vinkel.
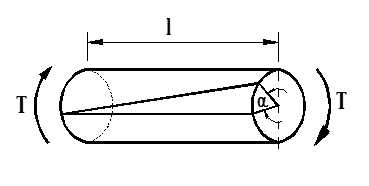
Vridningsvinkelen (α) er bestemt av:
α = $\frac{{T \cdot l}}{{{W_p} \cdot G \cdot r}}$
α = vridningsvinkel (rad)
T = vridningsmoment (Nm)
l = aksellengde (m)
G = skjærmodul (N/m2)
r = akselradius (m)
Skjærmodulen G er en materialkonstant som blir brukt ved vridningsberegninger på samme måte som elastisitetsmodulen E blir brukt ved strekk- og trykk beregninger. Sammenhengen mellom G og E er gitt ved:
G = $\frac{E}{{2 \cdot (1 + \mu )}}$
Her er (µ) = Poissons tall. For stål er µ ≈ 0,31. Dette gir skjærmodulen for stål (G):
G = $\frac{{210 \cdot {{10}^3}}}{{2 \cdot (1 + 0,31)}}$≈ 80 ⋅ 103 N/mm2 = 80 ⋅ 109 N/m2
Eksempel 1 – Vridning av aksler
En aksel med lengde l = 3 m blir belastet med et vridningsmoment T = 1500 Nm. Akselen er av stål og diameteren d = 80 mm. Bestem maksimal vridningsspenning og vridnings-vinkelen.
Polart motstandsmoment: Wp = $\frac{{\pi \cdot {d^3}}}{{16}}$ = $\frac{{\pi \cdot {{0,080}^3}}}{{16}}$ = 1,005 ⋅ 10-4 m3
Maksimal vridningsspenning:
τmaks = $\frac{T}{{{W_p}}}$=$\frac{{1500}}{{1,005 \cdot {{10}^{ - 4}}}}$ = 14,9 ⋅ 106 Pa = 14,9 N/m2
Vridningsvinkelen:
α = $\frac{{T \cdot l}}{{{W_p} \cdot G \cdot r}}$ = $\frac{{1500(Nm) \cdot 3(m)}}{{1,005 \cdot {{10}^{ - 4}}({m^3}) \cdot 80 \cdot {{10}^9}(Pa) \cdot 0,04(m)}}$ = 0,014 rad = 0,8°
Sammenhengen mellom dreiemoment og effekt er gitt ved:
T = $\frac{{{P_e}}}{{2 \cdot \pi \cdot n}}$ (Nm)
T = midlere dreiemoment (Nm)
Pe = akseleffekt (W)
n = rotasjonsfrekvens (s-1)
Eksempel 2 – Vridning av aksler
En maskinaksel skal overføre 30 kW ved n = 6,67 s-1.
a) Beregn nødvendig diameter når tillatt skjærspenning τtill = 50 N/mm2.
b) Bestem vridnings-vinkelen (α) når lengden l = 1 m.
Dreiemoment (T) = $\frac{{{P_e}}}{{2\pi n}}$= $\frac{{30 \cdot {{10}^3}(W)}}{{2 \cdot \pi \cdot 6,67({s^{ - 1}})}}$ = 716,2 Nm
Vi har at vridningsspenningen τtill = $\frac{T}{{{W_p}}}$ ⇒
Nødvendig motstandsmoment Wp = $\frac{T}{{{\tau _{till}}}}$= $\frac{{716,2 \cdot {{10}^3}}}{{50}}$= 14324 mm3
Wp = $\frac{{\pi \cdot {d^3}}}{{16}}$ = 14324 mm3 ⇒ d = $\sqrt[3]{{\frac{{16 \cdot 14324}}{\pi }}}$ $ \approx $42 mm
c) Vridningsvinkel (α) :
α = $\frac{\mathrm{T \cdot l}}{\mathrm{{W_p} \cdot G \cdot r}}$= $\frac{\mathrm{716,2(Nm)\cdot 1(m)}}{{\mathrm{14,3\cdot {{10}^{ - 6}}{(m^3)}}}\mathrm{\cdot{80}\cdot{10^9}{(N/m^2)}\cdot 0,021(m)\cdot}}$= 0,0298 rad. = 1,7°
Temperatur-spenninger
Ved oppvarming blir en maskindel større, og ved avkjøling krymper den. Dette utnytter vi i krympeforbindelser, der vi for eksempel krymper fast en aksel i et nav.
Figuren under viser en stålstang med lengde l som akkurat passer inn mellom to ufor-skyvbare avsteng. Stangen blir plassert mellom disse og så varmet opp 70°C.
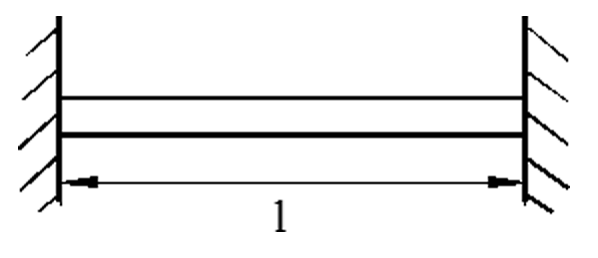
Dersom stangen kunne forlenge seg fritt, ville den få en forlengelse (Δl):
Δl = α ⋅ l ⋅ (t2 – t1)
Da av-stengene ikke kan forskyves, kan vi tenke oss at disse trykker stangen tilbake den samme strekningen (Δl).
Da kan vi sette:
Δl = α ⋅ l ⋅ (t2 – t1) = $\frac{{F \cdot l}}{{A \cdot E}}$ = σ ⋅ $\frac{l}{E}$ $ \Rightarrow $
Av dette finner vi spenningen som molekylene i stålstangen mobiliserer, når de blir påført trykk fra av stengene:
σt = α ⋅ E ⋅ (t2 – t1) (N/mm2)
Vi setter vridnings vinkelen α = 11⋅10-6 og elastisitetsmodulen E = 210 ⋅103 N/mm2.
Ved å varme opp stangen 70°C blir altså trykkspenningen:
σt = 11 ⋅ 10-6 ⋅ 70 ⋅ 210 ⋅ 103 = 161,7 N/mm2
Hvis stangen var fastholdt i endene og ble avkjølt 40°C, ville det på samme måte oppstå strekkspenninger i stangen.
Ved avkjøling (40°C) blir strekkspenningen:
σs = α ⋅ E ⋅ (t2 – t1) = 11 ⋅ 10-6 ⋅ 40 ⋅ 210 ⋅ 103 = 92,4 N/mm2
Temperaturspenning
Et varmtvannsrør av stål har godstykkelse 3 mm og er festet mellom to vegger A og B.
Monteringen av røret skjer ved romtemperatur + 20 °C. Røret skal transportere vann med temperatur + 90°C. Festet i veggene kan utføres på to måter:
1) Hull som er større en røret, (fritt opplagt).
2) Hull som er noe mindre enn rørets ytterdiameter, (fast innspent).
Ved 1) forlenges røret, mens det ved 2) oppstår en trykkspenning i materialet på grunn av den faste innspenningen. Beregn:
a) Forlengelsen i tilfelle 1)
b) Varmespenningen i tilfelle 2).
c) Kraften som gir like stor påkjenning som varmespenningen. (α = 12⋅10-6 per °C).
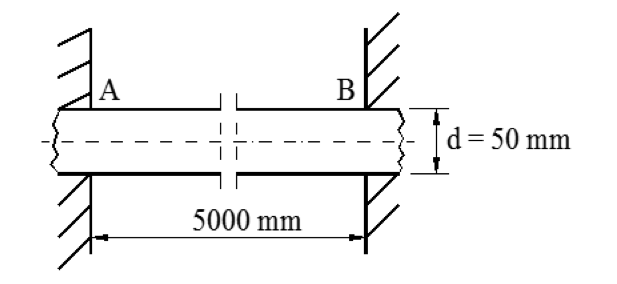
a) Fritt opplagt rør
Forlengelse av røret:
Δl = α ⋅ l ⋅ (t2 – t1) = 12 ⋅ 10-6 ⋅ 5000 ⋅ (90 – 20) = 4,2 mm
b) Fast innspent rør
Temperaturspenning i røret:
σt = α ⋅ E ⋅ (t2 - t1) = 12 ⋅ 10-6 ⋅ 210 ⋅ 103 ⋅ (90 – 20) = 176 N/mm2
c) Kraften (F) får vi av: σt = $\frac{F}{A}$ $ \Rightarrow $
F = σt ⋅ A = 176 ⋅ $\frac{{\pi \cdot ({{50}^2} - {{44}^2})}}{4}$ = 78 ⋅ 103 N = 78 kN
Anmerkning
I praksis vil temperaturen ikke bli 90°C i hele røret, men kanskje omkring 55°C (middelverdi). De virkelige spenningene blir derfor omtrent halvparten av det vi fant i eksempelet.
Måling av spenning - Strekklapper
Strekklapper blir brukt ved måling av spenninger i gods og dreiemoment på propellaksler mv. I prinsippet består strekklapper av tynne elektriske motstandselement, orientert i måleretningen.
Motstands-elementene er festet på et tynt underlag av epoksy, akryl eller bakelitt e.l., og blir limt fast på akselens overflate.
Virkemåten til strekklapper bygger på prinsippet om at resistansen i en elektrisk leder varierer når den strekkes, fordi tverrsnitts-arealet blir mindre og lengden større, men også fordi den spesifikke resistansen blir endret ved mekaniske deformasjoner.
Den elektriske resistansen endrer seg i prinsippet proporsjonalt med endring av lederens lengde, og vi får følgende sammenheng:
$\frac{\mathrm{R}}{\mathrm{R}}$ = $\mathrm{k}\frac{\mathrm{L}}{\mathrm{L}}$
R = strekklappens resistans
ΔR = endring av resistans
L = strekklappens lengde
ΔL = lengdeforandring
k = strekklappens følsomhet
Når en aksel blir påført et dreiemoment, vil den vris og det kan vises (sløyfes her) at hoved-spenningene[^5] alltid har en vinkel på 45° i forhold til akselens lengderetning. Det blir da strekkpåkjenning i den ene og trykkpåkjenning i den andre hovedretningen.
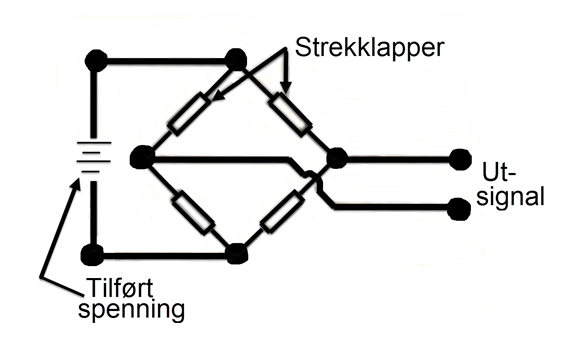
Strekklapper - Wheatstone bro
Et måleelement består vanligvis av flere strekklapper, koplet i en såkalt Wheatstone bro. Se figur.
Ved å tilknytte en ytre spenningskilde, kan vi måle motstandsendringen.
Ut-signalet fra broen blir som regel, overført trådløst til en stasjonær enhet, og basert på dette signalet kan vi beregne momentet når akselens diameter og materiale er kjent.
1.2.4 Utmatting og brudd mekanismer
Utmatting (materialtretthet)
En vanlig årsak til skade på maskinkomponenter er såkalt utmatting eller materialtretthet. Utmatting opptrer i komponenter som er utsatt for vekslende belastning, typiske eksempler er sylinderdeksler, stempelkroner, sylinderforinger, avgassventiler, akslinger og tannhjul mv.
Utmattingsbrudd arter seg ved at det etter en tids belastning (fra timer til år) utvikler seg en mikrosprekk i materialet. Mikrosprekken vokser til en litt større sprekk, og vi kommer over i en stabil sprekkvekst fase, der sprekken for hver belastningsveksling vokser et lite stykke.
Etter hvert som sprekken vokser blir det bærende arealet mindre og da den ytre belastningen er uendret, vil spenningen øke. På et tidspunkt blir spenningen lik materialets bruddgrense, og vi får et såkalt restbrudd. Dette arter seg som et plutselig og ofte uventet brudd i materialet, ofte kalt utmattingsbrudd. Figuren under illustrerer et utmattingsbrudd for en aksel.
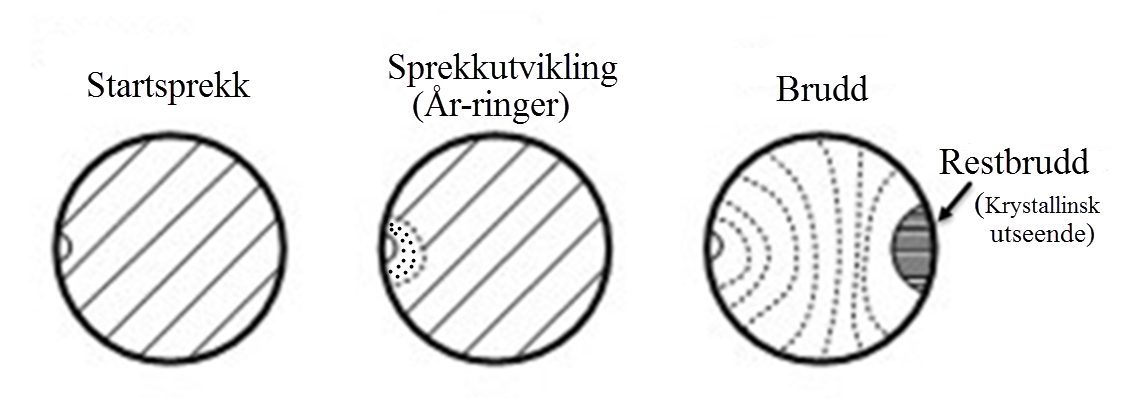
Forutsetningen for et utmattingsbrudd er at delen er utsatt for vekslende belastning og at belastningen setter opp strekkspenninger i materialet. Generelt gjelder at jo lavere spennings amplituden er, desto flere vekslinger vil materialet tåle før det oppstår sprekker eller brudd.
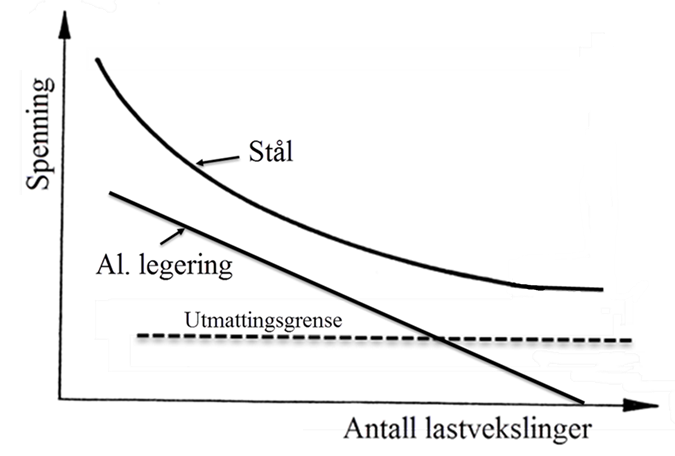
Utmattingsgrense
Sammenhengen mellom antall lastvekslinger til brudd og spenningsamplitude angis ofte ved en utmattingskurve eller «Wøhler» kurve, se figur.
Wøhler kurvens form avhenger av flere forhold, for eksempel:
- Overflate (polert flate gir økt levetid).
- Korrosivt miljø gir redusert levetid.
- Høy temperatur gir redusert levetid.
I enkelte tilfeller vil Wøhler kurven flate ut og bli horisontal for last-vekslingstall over et visst antall. Tilhørende spenningsverdi kaller vi utmattingsgrense. Er spenningen lavere, vil vi altså ikke få utmattingsbrudd i materialet.
En slik utmattingsgrense finner vi vanligvis for stål, men merk at det ikke alltid finnes en utmattingsgrense, dette gjelder for eksempel stål i sjøvann.
Det finnes også materialer som ikke har noen utmattingsgrense, de viktigste av disse er aluminium og aluminiumslegeringer. I slike materialer kan vi få utmattingsbrudd selv om spenningene er lave, bare antall vekslinger er høyt nok.
Elastisk og plastisk deformasjon
I alle metaller og metall-legeringer ordner atomene seg i et regelmessig, tredimensjonalt mønster kalt atomgitter eller krystallstruktur.
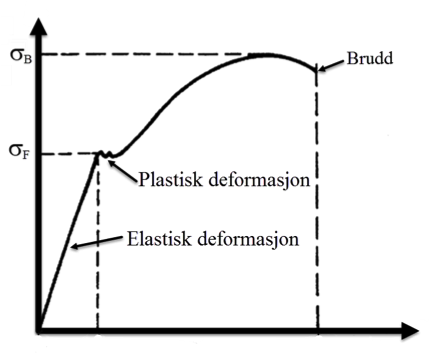
Dersom materialet blir påført belastninger under flytegrensen, oppstår det en deformasjon med bare små forandringer i atomgitteret.
Fjernes belastningen, går forandringen tilbake, deformasjonen er elastisk.
Ved belastninger som overskrider flyte-grensen, men ikke bruddgrensen, deformeres materialet varig. Det kalles plastisk deformasjon. Den metalliske sammenheng i materialet beholdes fortsatt, men forandringen i atomgitteret er større og ikke alltid reversibel om belastningen fjernes.
Økes imidlertid belastningen ytterligere, brytes til slutt den metalliske sammenheng og brudd oppstår, materialet er overbelastet.
Siging og sprøbrudd
Dersom et materiale utsettes for høye temperaturer og konstant strekkbelastning i lengre tid, kan det inntreffe en varig deformasjon eller brudd ved spenninger som er lavere enn flytegrensen (σF). Dette kaller vi siging.
Ved siging skjer deformasjonen både inne i kornene ved gliding mellom atomplanene og ved korngrensegliding. Ved lav temperatur har korngrensene den høyeste fasthet, men om temperaturen stiger, blir korngrensene svakere og kornene kan gli i forhold til hverandre langs korngrensene.
Et seigt brudd kan defineres som et relativt langsomt brudd som er ledsaget av betydelig plastisk deformasjon. Den plastiske deformasjonen skjer på makroskala og sees tydelig på selve bruddet, ved at bruddflatene har et matt utseende.
I motsetning til seigt brudd oppstår det ved sprøbrudd ingen makroskopisk deformasjon, og forplantningshastigheten er stor. Ved sprøbrudd skjer brudd ved kløving langs visse krystall plan og bruddflaten får derfor et krystallinsk utseende. Makroskopisk har bruddflaten også ofte et pil-mønster, der pilspissene peker mot startpunktet for bruddet.
For at et sprøbrudd skal kunne oppstå må følgende vilkår være oppfylt samtidig:
- Høy nominell spenning.
- Lav temperatur.
- Høy tri-aksial spenningstilstand.
- Høy belastningshastighet.
Dette betyr at risikoen for sprøbrudd ikke bare er avhengig av temperaturen, men også av indre og påførte spenninger og kjerver i materialet.
Vanligvis er kjerver, som har vært startpunkt for sprøbrudd, relativt skarpe da slike vil skape store spenningskonsentrasjoner.
Utmattingssprekker og sveisesprekker er de defekter vi vanligvis ser som startpunkter for sprøbrudd.
1.2.5 Innføring om svingninger (vibrasjoner)
Vi skal her kort beskrive og definere noen sentrale størrelser og begrep, brukt i forbindelse med vibrasjonsmåling og analyse av svingninger i maskineri og skrog.
Harmoniske svingninger (vibrasjoner)
Ved studie av vibrasjoner er det praktisk å ta utgangspunkt i såkalte harmoniske svingninger, som vi kan beskrive ved hjelp sinus funksjoner, definert som følger:
y = A ⋅ sin ωt ω = vinkelhastighet (rad/s)
Figuren under viser eksempel på en enkel sinuskurve, der y-aksen kan angis i en valgt enhet, for eksempel hastighet i mm/s, akselerasjon i mm/s2 eller (g).
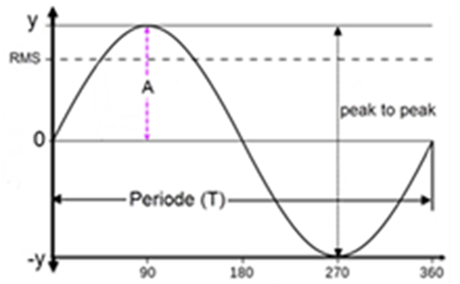
Vinkel i grader
A = amplitude i mm/s eller mm/s2
RMS ⇒ Root Mean Square, på norsk kalt effektiv-verdien.
RMS = $\frac{1}{\sqrt{2}}\mathrm{A}$ = 0,707⋅ A
T = svingetid (s)
f = frekvens (s−1)
RMS verdien eller effektiv-verdien er en karakteristisk størrelse for sinussvingninger, og blir ofte brukt som mål på svingningsutslaget istedenfor amplituden (A).
Egenfrekvens - definisjon
Egenfrekvensen, er den frekvens eller de frekvenser et svingedyktig system svinger med etter å være brakt ut av sin likevektsstilling. For et mekanisk system er egenfrekvensen bestemt ved massen som svinger og de elastiske krefter som driver massen tilbake til likevektsstillingen.
Et enkelt eksempel på egenfrekvens er en stemmegaffel. Når vi slår på gaffelen vil den svinge med en bestemt frekvens, som altså er gaffelens egenfrekvens.
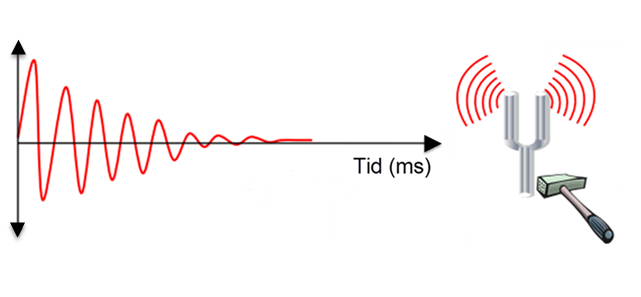
Egenfrekvens - mekaniske system
For å forklare begrepet egenfrekvens for mekaniske system, ser vi på et forenklet svinge-system:
En maskin med masse (m) er lagret til et fundament på to fjærer med fjærstivhet ($\frac{\mathrm{k}}{\mathrm{2}}$) som vist på figuren under. Vi ser bort fra dempning i systemet (d = 0).
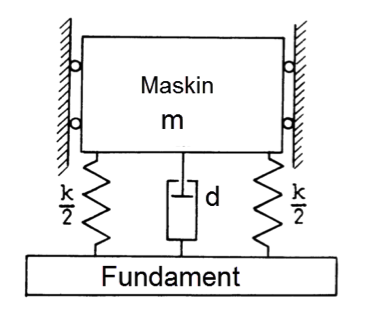
Bevegelsen settes i gang i vertikal retning ved å påføre en impulskraft og systemet blir så overlatt til seg selv.
Egenfrekvensen (fe) er bestemt av:
fe = $\frac{1}{2\pi}\sqrt{\frac{k}{m}}$ (s−1)
fe = egenfrekvensen i s−1 (hertz)
k = fjærstivhet i N/m (sum av 2 fjærer)
m = masse i kg
Dersom maskinen blir påført periodiske krefter med frekvens lik egenfrekvensen, oppstår det resonans, som teoretisk gir uendelig utslag. Men i praksis er det alltid dempning tilstede, slik at utslagene likevel blir begrenset.
Av formelen over ser vi at egenfrekvensen (fe) øker med økt stivhet av innfesting eller opplagring (økt k) og avtar med økt masse (m).
I praksis er det som regel, vanskelig å endre massen av en maskin eller utstyr, mens avstivning ofte er mulig.
Dersom vi for eksempel har sterke vibrasjoner i et skott eller en maskin om bord, kan vi ofte løse problemet ved å montere inn en ekstra stiver på skott eller maskinfeste. Egenfrekvensen blir da endret slik at vi unngår resonans.
Merk imidlertid at dersom vi forsterker et skott e.l. for å stoppe vibrasjonen, så vil impuls-kreftene som forårsaket vibrasjonene, fortsatt være tilstede i skrog og innredning mv., noe som kan føre til at vibrasjonene «flyttes» til en annen maskin eller skott i nærheten.
Egenfrekvensen for virkelige skott og maskiner er ofte vanskelig eller umulig å beregne, men i praksis kan vi likevel ha god nytte av ovennevnte formel som en tommelregel[^6] :
Avstivning gir altså økt egenfrekvens og er et mulig tiltak mot lokale resonans svingninger.
Noter
[4]: S er et karakteristisk belastningstall for lager-smøring.
[5]: Merk at akselbrudd alltid skjer i en vinkel på ca. 45° av lengde-retningen.
|6]: AL har, med hell, brukt regelen i praksis.

