2. Stabilitet (9 sp) ant. arbeidskrav 3
2.1.1 Definere KG, KM, GM og GZ. Vise hvordan de fremkommer og forklare den virkning vektfordelingen om bord og skipets form og fribord har på størrelsene.
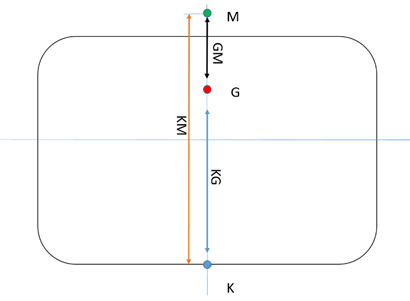

Bildet er hentet fra formelsamlingen på marfag.
Vi deler stabilitetsberegningene inn i statisk og dynamisk stabilitet.
Initialstabilitet
Initialstabilitet er statisk stabilitet som blir beregnet (ved små krengninger) under krengeprøve for å finne lettskips GM0.
Initialstabilitet kan også forklares som «begynnelsesstabilitet» opp til krengevinkel 2-3°. Dette gjelder også beregning av GM0.
Statisk stabilitet
Statisk stabilitet viser hvordan fartøyet oppfører seg når det vært utsatt for statiske krefter, som for eksempel lasting/lossing eller flytting av vekter.
Dynamisk stabilitet
Dynamisk stabilitet viser hvordan fartøyet oppfører seg på grunn av en energi som blir tilført, f.eks.: dersom man mister et lodd på dekk eller ytre krefter som vind og bølger.
Arealet under GZ-kurven viser energien som må tilføyes for å krenge skipet og denne beregnes som dynamisk stabilitet.
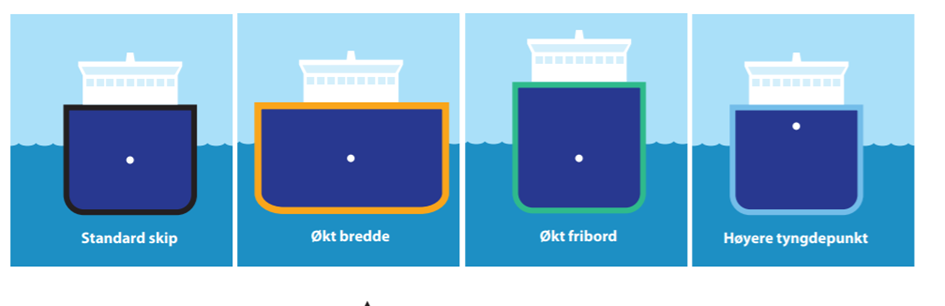
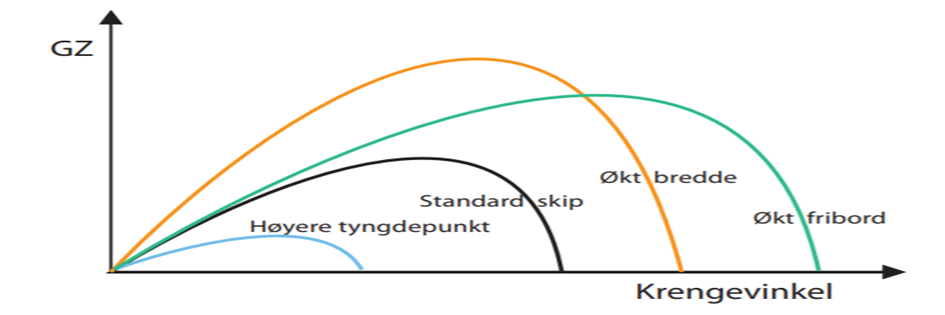
Dersom en ser på figuren av GZ-kurven som indikerer standard skip, økt bredde, økt fribord og høyere tyngdepunkt er det en feil (Bilde tatt fra K 12, Marfag).
Kan du finne feilen?
Svar: Økt bredde er feil
På figurene under ser vi hvordan krengningen vil utspille seg på to like skip med forskjellige bredder og samme krengevinkel.
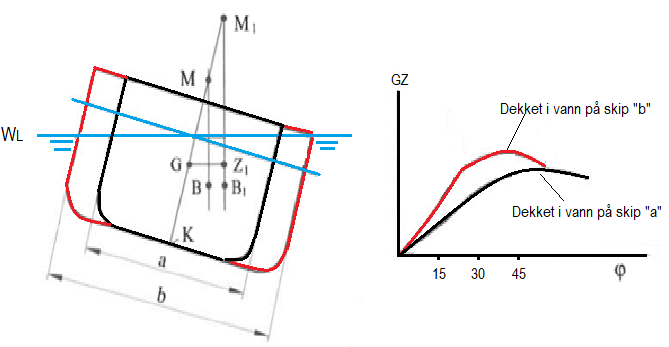
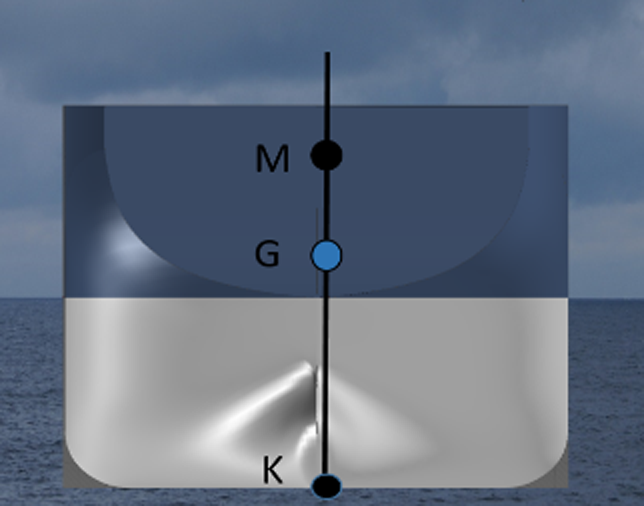
På figuren til venstre kommer det frem dersom skipets bredde a, ville oppdrift senteret flytte seg til B og metasentret ligge i M.
Dersom skipet hadde bredde b, ville oppdriftssenteret gått til B1 og metasentret ligge i M1 - som er mye høyere.

Kasseformet fartøy K = 12 for andre fartøy K<12
Vi ser at GZ-armen øker med økt bredde, inntil dekkshjørnet kommer under vann.
Stor bredde gir altså god formstabilitet.
Desto bredere skipet er jo før kommer dekket i vann. Stabiliteten utstrekning kommer derfor til å minske når bredden øker.
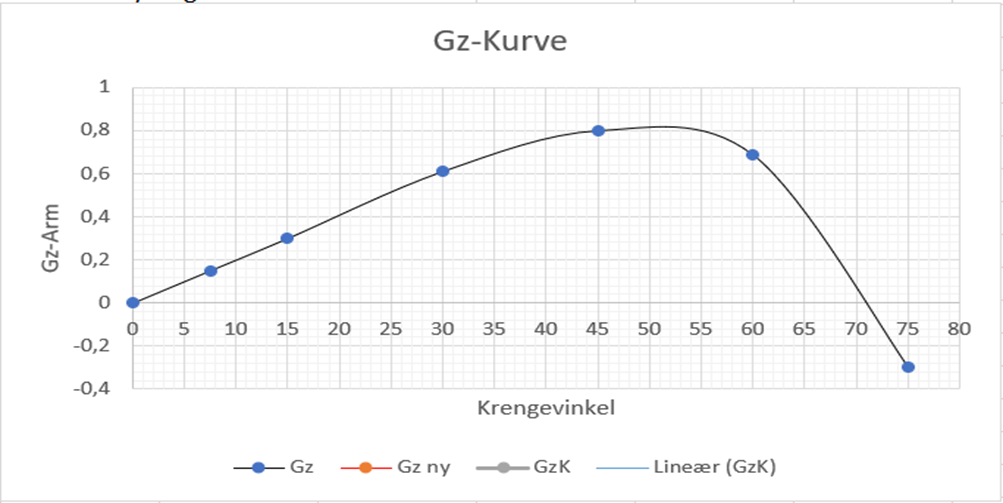
Stabilitetens utstrekning er i dette tilfellet fra 0 - 71°.
Stabilitetskrav:

2.1.2 Beregne GM av: GM = KM - KG
a) Tegn et tverrskips av en lekter med dypgående på 6 meter og fribord 5 meter. Og sett ut KG 5 meter og KM 5.5 m. Sett ut B, finn GM og dybde i riss?
Svar: 0,5 mb) Dersom skipet har en KM 5.60 meter og en KG 5.10 m, hva blir skipets GM?
Svar: 0,5 mc) Et skip har en KM på 7,0 meter og en GM på 0.25 meter hva er skipets KG?
Svar: 6.75 md) Et skip har en KM på 5,40 meter og en KG på 5,50 meter, hva er GM? Hva vil skje med dette skipet? Tilfredsstiller det kravet til stabilitet?
Svar: -0,10 m/Nei
2.1.3. Definere begrepene positiv, negativ og labil stabilitet
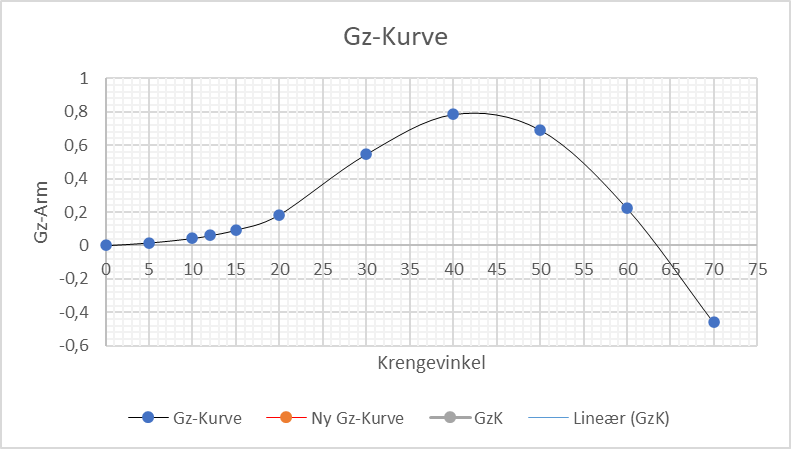
Her vil jeg vise tre alternativer, vi skal vise GZ-kurve med en GM på - 0,20 meter og en GM 0 meter og en GM på 0,20 meter, deplasementet er 50 000 tonn på M/S Sidus.
Labil likevekt GM = 0 m
Ustabil GM < 0 m (-0,20 m)
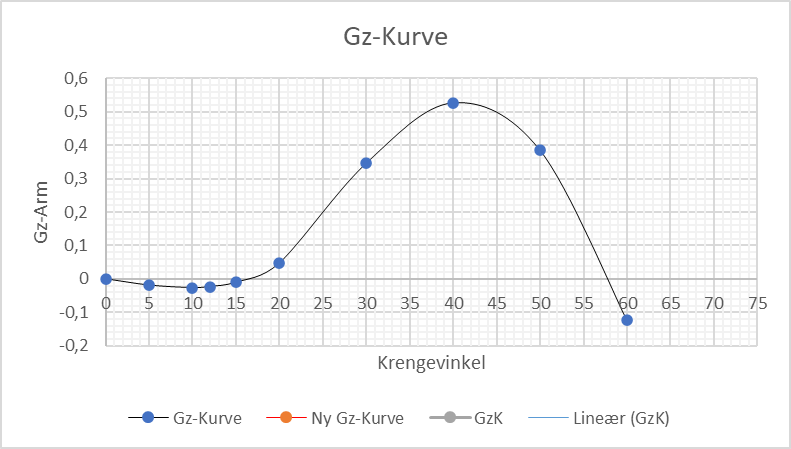
Stabil GM > 0 m (0,20 m)
Oppgave 1.
Hva er stabilitetens utstrekning på de tre eksemplene over (labil likevekt, ustabil GM og stabil GM)?
2.1.4 Forklare hvordan skipets evne til å motstå krengning er avhengig av GM (metasenterhøyden), og hvordan skipets evne til å rette seg under krengning er avhengig av GZ-armen (den rettende arm)
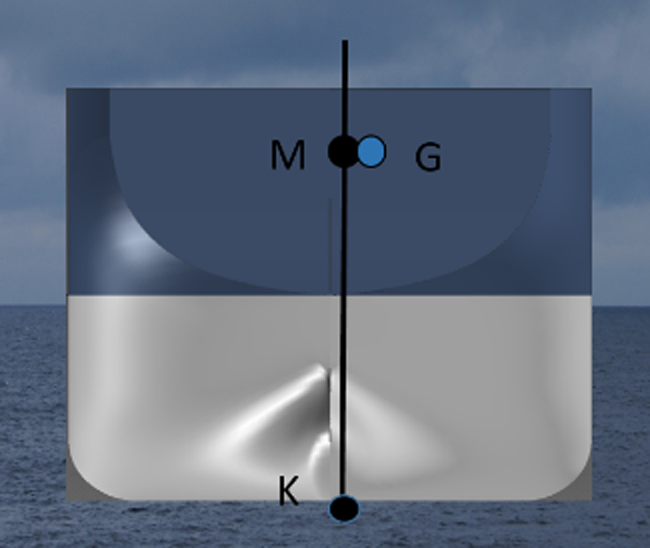
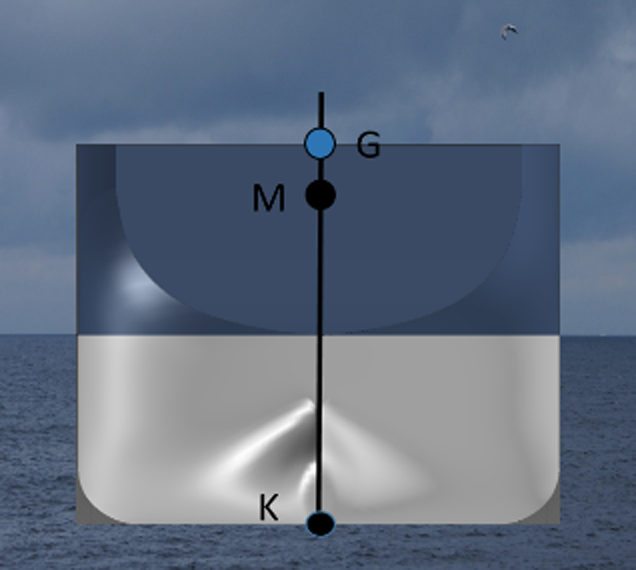
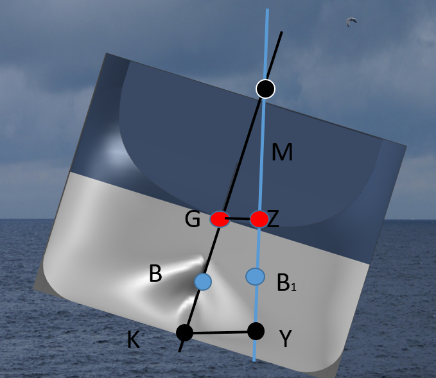
Når vi ser på bilde under, ser vi at det er stor avstand mellom G og M som gir større arm mellom G og Z ved krengning. Det er avstanden mellom G og Z som fortell oss hvor stor kraft skipet har til rådighet for å rette seg opp (MR). Desto større GM desto større GZ- arm.
Rettende moment MR: MR= ∆ x GZ
Eksempel: M/S Sidus, ∆ 50 000 tonn, tar ut verdiene fra GZ-kurven, GZ 30° på stabil GM (GM 0,20 m) under punkt 2.1.3. GZ 30° = 0,58 m. MR= ∆ x GZ = 50 000 tonn x 0,58 m = 29 000 tm (som vil jobbe med å rette opp skipet).
Tar ut verdier fra GZ-kurve, GZ 30° på labil GM (GM 0,0 m) under punkt 2.1.3. GZ 30°. GZ 30° = 0,42 m. MR= ∆ x GZ = 50 000 tonn x 0,42 m = 21 000 tm (som vil jobbe med å rette opp skipet).
Konklusjon er, dersom vi reduserer GM med 0,20 meter så reduserer vi det rettende moment ved GZ 30° med 8 000 tm.
Oppgave 1
M/S Sidus er lastet til ∆ 30 000 tonn og har en GZ-arme ved 30° på 0,30 m
a) Hva blir det rettende moment ved 30° krengning?
Svar: 9000 tm
Oppgave 2
M/S Sidus er lastet til ∆ sommer og har en GZ- arm ved 30 grader krengning på 1,2 meter.
a) Hva blir det rettende moment ved 30° krengning?
Svar: 63817,2 tm
Oppgave 3
a) Hva menes med det rettende moment?
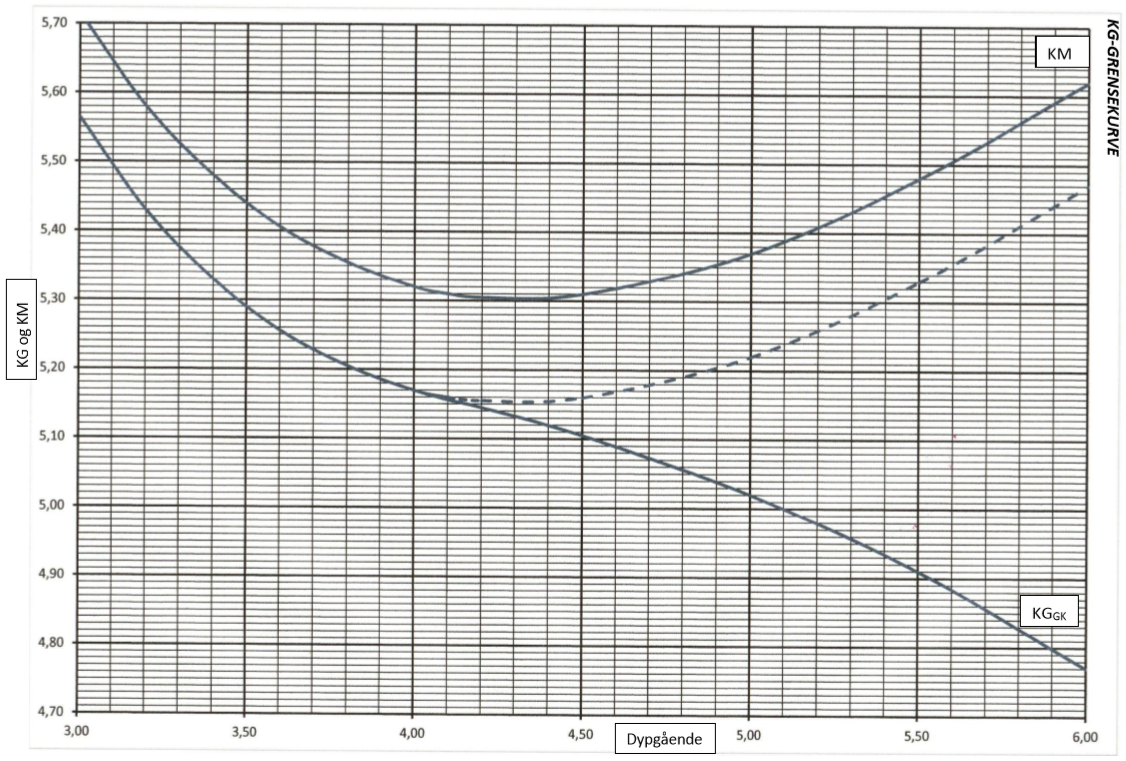
2.1.5 Beskrive bruken av kurver/tabeller for KM, GZ og maksimalt tillatt KG (KG-grensekurver).
Med KG - grenseverdi forstår vi størst tillatte KG for bestemte deplasement eller dypgang, slik KG- grenseverdier blir beregnet av byggeverftet. De er basert på gjeldende stabilitetskrav for skip og blir presentert i form av en tabell eller kurve.
Eksempel på KG - grensekurve laget for M/S Linda
Eksempel på KG og KM grensekurve
Eksempel på plansje for en eldre «Båt» Skip.
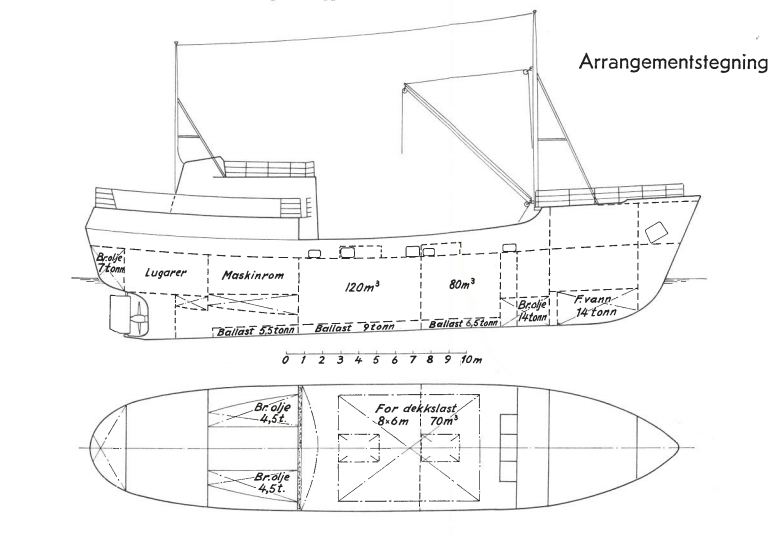
Informasjon om skipet
Informasjon om skipet: LOA 33,90 m
-
LPP 29,85 m
-
Bredde moulded: 7,00 m
-
D 3,90 m
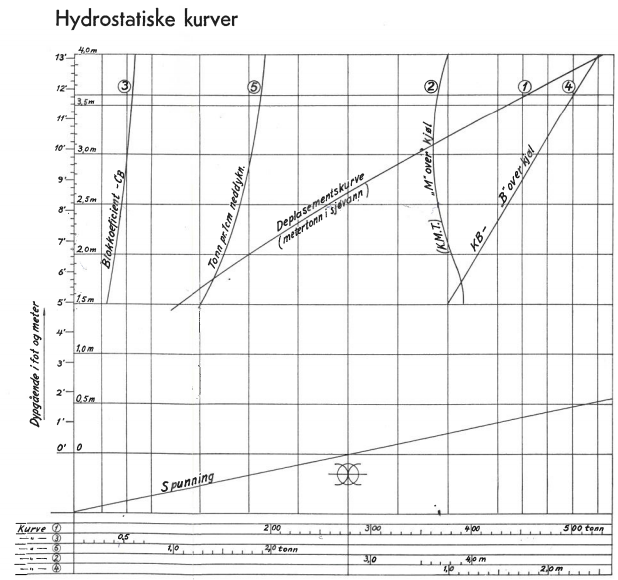
Oppgaver med bruk av Hydrostatisk kurve:
Oppgave 1
Du skal laste til 2,7 meter «even keel».
Ta ut hydrostatisk data for dette dypgående?
Oppgave 2.
a) Finn BM når en har lastet til 3 meter?
b) Hva er ∆ ved denne dypgangen?
c) Hva er CB på denne dypgangen og hvorfor er den så liten?
d) Hva er TPC'en på denne dypgangen?
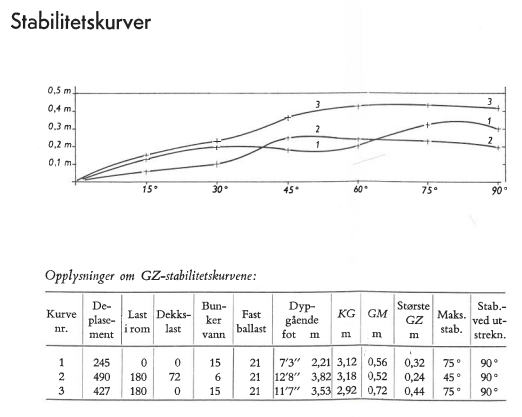
Oppgave 3
Under opplysninger om GZ- stabilitetskurve ser vi at stabiliteten er best på kondisjon 3 (KURVE NR. 3)
Hvorfor er den best her og dårligst på kondisjon nummer?
2.1.6. Beregne KG av formelen: KG = Sum vertikalmomenter / ∆
Oppgave 1 Beregning av KG ut ifra lett skip
Et skip har deplasement som lett skip på 350 tonn, KG 3.5 m.
Følgende vekter blir lastet:
| Diesel | 25 tonn | Tyngdepunktets høyde over kjøl 1,0 m |
| Ferskvann | 5 tonn | Tyngdepunktets høyde over kjøl 1.5 m |
| Last i rom # 1 | 120 tonn | Tyngdepunktets høyde over kjøl 3.8 m |
| Last i rom # 2 | 150 tonn | Tyngdepunktets høyde over kjøl 3.6 m |
| Last på dekk | 25 tonn | Tyngdepunktets høyde over kjøl 7.1 m |
a) Beregne skipets KG og GM etter lasting når KM er 4.15 m?
Svar: KG = 3,6 m, GM = 0,55 mb) Hvordan anser du skipets stabilitet etter lasting?
c) Hvor stor er opprettende moment ved 30° når GZ - armen er 0.275 m?
Svar: 185,6 tm
Oppgave 2 Beregning av KG etter lossing
Et skip ligger ved kai og losser. Deplasement lett skip er 550 tonn og total dødvekt før lossing er 450 tonn. KG er utregnet til 4.25 m før lossing.
Følgende vekter blir losset:
| Rom # 1 | 150 tonn. | Tyngdepunkt (VCG/KG) 4.32 m over kjølen |
| Rom # 2 | 180 tonn. | Tyngdepunkt (VCG/KG) 4.20 m over kjølen |
| Dekkslast | 75 tonn. | Tyngdepunkt (VCG/KG) 7.10 m over kjølen |
a) Beregne skipets KG og GM etter lossing når KM er 4.55 m?
Svar: KG = 3,89 m, GM = 0,66 mb) Hvordan vurderer du stabiliteten etter lossing?
c) Hva ville du gjøre hvis det var aktuelt å forbedre stabiliteten før avgang?
Oppgave 3 Beregning deplasement og felles tyngdepunkt for dødvekten
Et fartøy har følgende data:
Dødvekt ........................... 2650 tonn.
LPP....................................... 70,00 m
Bredde................................. 12.50 m
Dybde i riss........................... 7.50 m
Dypgang lastet....................... 6.75 m
CB lastet................................ 0.61
KG lastet................................ 5.90 m
KG lett skip............................ 5.60 m
KM lastet............................... 6.25 m
a) Beregne skipets deplasement lastet og lett skip?
Svar: ∆ = 3692,9 tonn & L.S = 1042,9 tonnb) Beregne skipets GM lastet?
Svar: GM = 0,35 mc) Hvor høyt over kjølen ligger gjennomsnittlig tyngdepunkt for lasten?
Svar: KG last 6,01 m
Tyngdepunkt i lasterom
Oppgave 4. M/S Sidus
a) Finn vcg/Kg når det er 2000 tonn i hvert av rommene 1 & 10 med en SF 1.28 m³/t.
Svar: # 1 = 9.1728 m # 10 = 15.937 mb) Hva er ullasje, VCG/Kg og høyden på lasten i rom 1 når du har 2000 m³?
Svar: U-8,04 m, H-11,06 m, VCG-7,826 m
Oppgave 5. M/S Linda
a) Finn vcg/Kg når det er 2050 m³ i rom 2 og 6, lasten er bales.
Svar: #2 - 4,875 m, #6 - 4,90 mb) Finn vcg/Kg i rom 1 når rommet er lastet med en løs bulklast som stuer 1,6 m³/t og det skal være 1200 tonn i rommet.
Svar: 5,77 m
2.1.7 Beregne endring i KG når en vekt skiftes vertikalt av formelen: GG1 = (vekt x avstand) / Depl.
Oppgave 1. Flytting av last og forandring i KG
Et skip er ferdig lastet og deplasementet er 3500 tonn. KG beregnet til 4.75 m.
Man ønsker imidlertid å forbedre stabiliteten ved å flytte 5 kontainere a 5 tonn fra dekk og ned i underrommet. Avstand fra dekk til underrommet regnes til 5.5 meter.
a) Hvor mye ble skipets G senket som følge flytting av lasten?
Svar: GG1 = 0,039 mb) Hva ble KG etter flytting?
Svar: KG = 4,711 m
Oppgave 2. Flytting av last og forandring i KG
Det skal flyttes en last på 350 tonn fra dekke ned i lasterommet. Avstanden er beregnet til 10 meter. KG før flytting var beregnet til 8.20 meter og deplasementet er på 9000 tonn.
a) Hva blir KG etter flytting?
Svar: 7,812 m
Oppgave 3. Flytting av last og forandring i KG
Det skal flyttes en last på 150 tonn fra laste rommet opp på dekk grunnet vedlikehold i lasterommet. Lasten Kg før flytting var 2 meter og ny Kg på lasten etter flytting er beregnet til 14 meter. Skipets KG var beregnet til 8 meter før flytting og KM til 8.5 meter. Skipets ∆ 3000 tonn.
a) Har skipet tilstrekkelig med stabilitet etter lasten er flyttet?
Svar -0,10 m/Nei
Oppgave 4. Flytting av last
M/S Linda har et deplasement på 18 300 tonn og VCG/KG på 8,10 meter. Skipet fører dekkslast. En ønsker å flytte 500 tonn av dekkslasten ned i det ene lasterommet som er tomt. Dekkslasten vcg er 13,55 meter. Når lasten flyttes ned i lasterommet vil den få en ny vcg på 4,25 meter.
a) Hvor mye og hvilken vei flytter tyngdepunktet seg?
Svar: GG1 = 0,254 m nedoverb) Hva blir nytt tyngdepunkt?
Svar: KG1 = 7,846 mc) Hva blir ny GM?
Svar: G1M = 0,674 m
2.1.8. Beregne endring i KG når en vekt tas inn eller ut av formelen: GG1 = (vekt x avst. til G) / (Depl +/- vekt)
Oppgave 1. Beregning av GG1 ved lossing av mindre partier
Et skip ankommer havn for lossing av en kontainer. Skipets deplasement er 1250 tonn og KM er lik 5.30 m samt GM 0.55 m. Kontaineren veier 15 tonn og er plassert på dekk slik at Kg er 3.5 m.
a) Beregne skipets KG før lossing?
Svar: KG = 4,75 mb) Finn skipets KG etter lossing?
Svar: KG = 4,77 m
Oppgave 2. Beregning av GG1 ved lasting av mindre partier
Et skip ankommer havn for å laste en kontainer som veier 12.5 tonn. Denne stues på dekk med et tyngdepunkt 8 m over skipets kjøl. Deplasement før lasting var 4000 tonn og KG 5.00 m.
a) Beregne GG1 som følge av lastingen?
Svar: KG = 5,01 mb) Finn ny GM, når KM etter lasting er lik 5.65 m?
Svar: GM = 0,64 m
Oppgave 3.Beregning av skipets G
Et skip har et deplasement på 5000 tonn og en beregnet KG på 9,4 meter. Det skal tas om bord en last på 120 tonn som er plassert 5 meter under skipets tyngdepunkt.
a) Hva blir ny KG etter lasten er tatt om bord?
Svar: 9,28 m
Oppgave 4. Beregning av skipets G
Et skip har et deplasement på 16 000 tonn og et tyngdepunkt (vertikalt) på 8 meter. Vi tar om bord en last på 200 tonn som plasseres 4,5 meter under skipets tyngdepunkt (G)
a) Hva blir skipets KG etter lasting?
Svar: 7.944 m
Oppgave 5. Beregning av skipets G
Et skip har et deplasement på 3000 tonn og en beregnet KG på 9,5 meter. Det skal losses en last på 100 tonn som har en KG på 2.5 meter. KM etter lossing er 10 meter.
a) Hvor mye flytter skipets tyngdepunkt seg?
Svar: 0,24 mb) Hva blir ny KG og GM etter lossing?
Svar: 9,74 m/0,26 m
Oppgave 6. Beregning av skipets KG
M/S Mercandian Importer har et deplasement på 3 500 tonn og skal losse 700 tonn fra Hold no: 1. Skipets KG før lossing er beregnet til 4.94 meter.
a) Hva blir ny KG etter lossing?
Svar: 5,473 mb) Hva er skipets GM etter lossing?
Svar: – 0,163 m
Oppgave 7. Beregning av skipets KG
M/S Linda har et deplasement på 20 150 tonn og KG er beregnet til 8,10 meter. Vi tar om bord en last på 3 000 tonn som plasseres 5 meter under skipets tyngdepunkt.
a) Hva blir ny KG?
Svar: KG = 7,452 m
Oppgave 8. Beregning av skipets KG etter flytting
M/S Linda har et deplasement på 15 010 tonn og KG er beregnet til 8,05 meter. Vi flytter en last på 300 tonn fra lasterommet til dekket. Avstanden er 15 meter.
a) Hva blir ny GG1?
Svar: GG1 = 0,3 mb) Hva blir ny KG1?
Svar: KG1 = 8,35 mc) Hva blir GM?
Svar: GM = 0,2 m
2.1.9 Beregne vekt som må skiftes/lastes/losses i gitt posisjon for ønsket endring av KG.
Oppgave 1. Endring av KG
M/S Linda har et deplasement på 12 380 tonn og KG er beregnet til 8,15 meter, vi ønsker å senke skipets tyngdepunkt med 0,2 meter ved å flytte en last som er plassert 18 meter over kjølen til 8 meter over kjølen.
a) Hvor mye vekt må vi flytte?
Svar: 247,6 tonn
Oppgave 2. Endring av skipets tyngdepunkt ved lossing av dekkslast
Mercandian Importer har et deplasement på 4110 tonn og en GM på 0,16 m. Skipets kaptein ber deg om å losse en del av dekkslasten, da det er ventet dårlig vær på neste reise. Kapteinen ønsker en GM på minimum 0,25 m. Tyngdepunktet til dekkslasten er beregnet til 9,60 meter.
a) Hvor mye må du losse for å oppnå ønsket GM?
Svar: 85,9 tonn
Oppgave 3. Endring av skipets tyngdepunkt ved lasting av dekkslast
Mercandian Importer har et deplasement på 3970 tonn og en GM 0.38 meter. Det skal tas om bord dekkslast. Skipet ligger i sommersone, kapteinen vil ta med så mye dekkslast som mulig. Kg for dekkslasten er estimert til 9,80 meter, kapteinen vil ha minimum GM på 0,25 meter ved avgang.
b) Hvor mye kan du laste, med tanke på kapteinens ønske?
Svar: 113,4 tonn
2.1.10 Beskrive at skipet ligger i stabil likevekt når skipets tyngdepunkt og oppdriftssenter virker i samme vertikal.
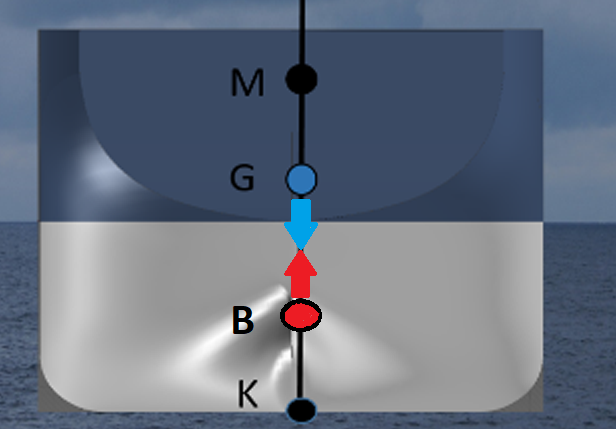
Her ligger skipet i stabil likevekt tverrskips, oppdrift senteret virker opp mens tyngdepunktet virker ned i samme vertikale linje, dette kalles stabil likevekt. Dersom skipet nå begynner å krenge vil B (oppdrift senteret) flytte seg ut til den siden skipet krenger, da vil ikke skipet være i stabil likevekt. Se figur under punkt 2.1.4. I dette tilfelle måles verdien til B og G fra kjølen, derfor kaller vi de KG og KB.
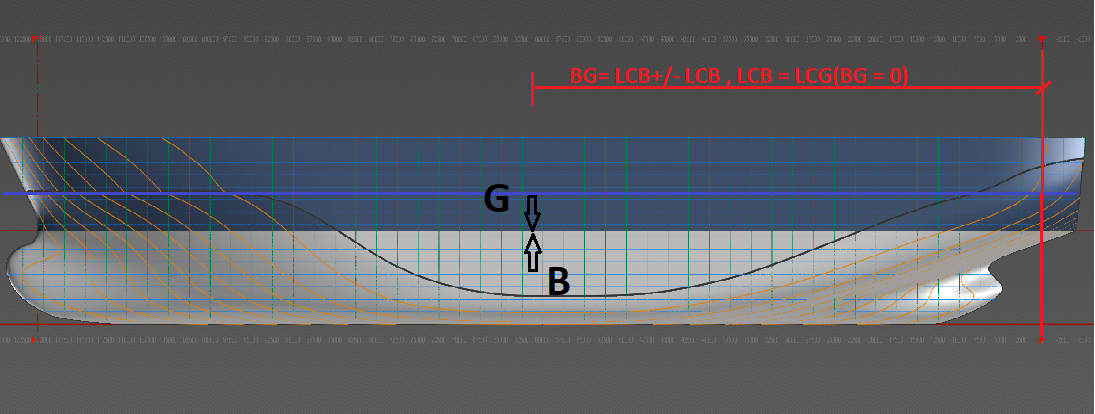
Her ligger skipet i stabil likevekt langskips, oppdrift senteret virker opp mens tyngdepunktet virker ned i samme vertikale linje, dette kalles stabil likevekt. Dersom en nå skal trimme skipet må en flytte G enten forut eller akterut. Dersom G flyttes vil skipet trimme, flyttes tyngdepunktet forut vil skipe få en forlig trim. Men dersom en flytter tyngdepunktet akterut vil en få en akterlig trim og skipet vil ikke være i stabil likevekt lengre. I dette tilfellet måles avstanden fra Ap (Akter perpendikulær) rorstammen. Derfor kalles de LCG og LCB, som står for langskipsenterets tyngdepunkt og langskipsenteret for oppdrift.
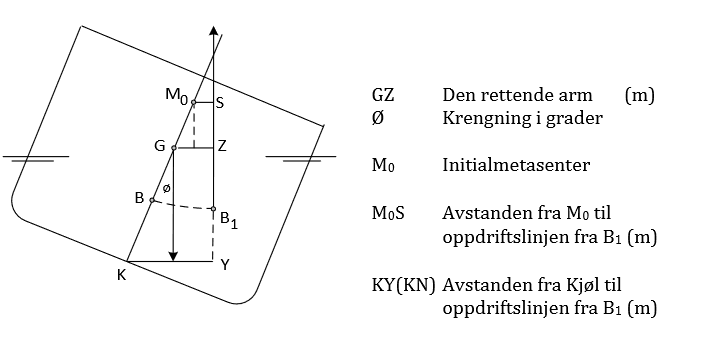
2.1.11 Beregne GZ-kurven av formlene: GZ = KY (KN) - KG • SinØ & GZ = GM • sinØ + M0S
Oppgave 1. GZ-kurve
Et skip har et deplasement på 25 600 tonn. KM er 9,32 meter og GM er beregnet til 1,23 meter. KY - verdier for denne lastekondisjonen er som følgende for krengningene som er angitt i grader under:

a) Hva blir skipets KG?
Svar: KG 8,09 mb) Tegn GZ-kurve for denne lastetilstanden?
c) Hva blir stabilitetens utstrekning?
Svar: 0 - 67°d) Hva blir dynamisk stabilitet?
Svar: 0-30° = 0,11 m.rad, 30 - 40° = 0,116 m.rad & 0 - 40° = 0,228 m.rad
Oppgave 2. M/S Linda GZ-kurve
M/S Linda har et referansedypgående på 8,30 meter og en GM 0,55 meter KY - verdiene i denne kondisjonen er som føler:

a) Lag GZ-kurve for denne kondisjonen.
b) Tilfredsstiller Linda alle stabilitetskravene i henholdt til regelverket?
Svar: Ja
Oppgave 3. M/S Sidus GZ-kurve
M/S Sidus har et deplasement på 30 400 tonn, skipets GM er beregnet til 0,70 meter.
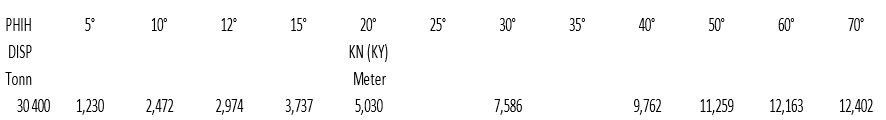
a) Lag GZ-kurve, sjekk at M/S Sidus tilfredsstiller krava til stabilitet?
(Svar: Ja)
Oppgave 4. Mercandian Importer GZ-Kurve
M/S Mercandian Importer har et referansedypgående på 5,64 meter og en GM på 0,68 meter, skipet har følgende M0S verdier.

a) Lag GZ-kurve, sjekk at M/S Mercandian Importer tilfredsstiller krava til stabilitet
Svar: Ja
Oppgave 5. GZ-kurve og dynamisk stabilitet
Et skip har et deplasement på 28 005 tonn med et samlet vertikalmomenet på 225 619 tm. Det skal bunkre og ta om bord stores. Skipet bunkrer følgende:
| Tank | vekt (t) | Vcg (m) |
|---|---|---|
| DB tank 3 | 800 | 0,90 |
| DB tank 5 | 1200 | 0,80 |
| DB tank 6 | 900 | 0,80 |
| Ferskvannstank | 300 | 9,75 |
Det tas om bord 100 tonn stores med en beregnet vcg på 10.05 meter.
På grunn av to slakke tanker må en korrigere for fri væskeoverflate. Denne korreksjonen er beregnet til 0.37 meter. KM etter bunkring og stores tatt om bord er 8,18 meter.
a) Hva blir KG2 etter at stores og bunkringen er ferdig?
Svar: KG2 = 7,779 m
KY- verdiene for denne lastekondisjonen er som følge:
| Krengning i grader | 7,5 | 15 | 30 | 45 | 60 | 75 |
|---|---|---|---|---|---|---|
| KY - Verdier i meter | 1,100 | 2,273 | 4,571 | 6,302 | 7,001 | 7,113 |
b) Tegn GZ-kurve for denne lastetilstanden.
c) Regn ut dynamisk stabilitet og kontroller mot regelkrav.
Svar: 0-30° = 0,157 m.rad, 30-40° = 0,1237 m.rad & 0-40° = 0,285 m.rad
Oppgave 6. GZ-kurve og dynamisk stabilitet
Et skip skal laste til sommermerket. Ved merket er skipets totale dødvekt 26 000 tonn.
Av dødvekten er 21 500 tonn last, som er plassert i lasterom 1, 2, 3, 4, 5 og 6. for lasterom 1 til 5 er det en samlet last 18 700 tonn og vertikalmomentet beregnet til 152 000 tm. Vcg for lasterom 6 er beregnet til 8,00 meter.
Resterende del av skipet dødvekt består av 1 000 tonn tungolje i DB tank 3, 1000 tonn tungolje i DB tank 5, 2000 m³ med dieselolje, som har en tetthet på 0,90 t/m³, på DB tank 6, 500 tonn ferskvann i ferskvannstanken og 200 tonn stores med en beregnet vcg til 10,05 meter.
Opplysninger som gjelder tankene og lettskips (L/S) data:
| Tank | Vcg |
|---|---|
| DB tank 3 | 0,85 meter |
| DB tank 5 | 0,85 meter |
| DB tank 6 | 0,85 meter |
| Ferskvannstank | 10,75 meter |
| Lett skip data: | |
| Deplasement | 5 120 tonn |
| Dypgående forut | 0,62 meter |
| Dypgående akterut | 5,22 meter |
| Dypgående midtskips | 2,92 meter |
| Vcg | 8,65 meter |
På grunn av to slakke tanker må en korrigere for fri væskeoverflate. Denne korreksjonen er beregnet til 0,4 meter. KM er beregnet til 8,20 meter etter lasting.
a) Ta utgangspunkt i lett skip (L/S) og fullfør lastingen og regn ut KG etter lasting
Svar: KG1 = 7,368 m
KY- verdiene for denne lastekondisjonen er som følger:
| Krengning i grader | 7,5 | 15 | 30 | 45 | 60 | 75 |
|---|---|---|---|---|---|---|
| KY - Verdier i meter | 1,130 | 2,251 | 4,322 | 6,008 | 6,750 | 6,901 |
b) Tegn GZ-Kurve for denne lastetilstanden.
c) Regn ut dynamisk stabilitet og kontroller opp mot regelverket.
Svar: 0-30° = 0,121 m.rad, 30-40° = 0,0829 m.rad & 0- 40° = 0,204 m.rad
2.1.12 Korrigere en gitt GZ-kurve: G1Z1 = GZ ± GG1• sinØ, der GG1 er avvik i KG
Oppgave 1. Korrigering av GZ-Kurve på Mercandian Importer
Det skal tas om bord en dekkslast på 100 tonn før skipe går i fra kai, Mercandian Importer har følgende deplasement før restlast tas om bord, ∆ 3731 tonn. Dekkslasten vcg er beregnet til 9 meter.
a) Hva er skipets GM før en tar om bord dekkslasten?
Svar: 0,50 mb) Korriger GZ-kurven ved lasting av ny last. Tilfredsstiller vi stabilitetskrava (se bort ifra dynamisk)?
Svar: Tilfredsstiller ikke alle kravene til stabilitetc) Hva er stabilitetens utstrekning etter en har tatt om bord lasten?
Svar: 0 - 55°d) Er det noe vi kunne gjort for å bedre skipets stabilitet?
Oppgave 2. Korrigering av GZ-kurve grunnet vanninntrenging i lasterom
Det har kommet vann ned i lasterom 1, det er beregnet at det totalt har kommet 200 tonn, og dette utgjør en FS-moment på 1800 tm. Vcg for lasterommet er 3 meter. Skipets deplasement er beregnet til 15 000 tonn før vanninntrenging i lasterom 1. KM er 7 meter før og etter vanninntrenging.

a) Finn cirka GM ut ifra GZ-kurven.
Svar: 1,18 mb) Korriger GZ-kurven, er stabiliteten fortsatt innenfor kravet?
Svar: Ja
2.1.13 Beskrive virkningen av frie væskeoverflater på stabiliteten og beregne stabilitetsreduksjonen av formelen: GG2 = (IT • ρ) / Depl. ρ = væskens densitet
Oppgave 1. Fri væskeoverflate av bunkerstank
Et skip har en slakk tank som er 12 meter langt og 9 meter bred. Tanken inneholder bunkers med tetthet på 0,915 tonn/m³. Skipet har et deplasement på 6 785 tonn.
a) Hvor mye reduseres GM på grunn av denne slakke tanken?
Svar: GG2 = 0,098 m
Oppgave 2. Fri væskeoverflate av ballasttank
Et skip har et volumdeplasement på 5 000 m³ og seiler i brakkvann med en tetthet på 1,017 tonn/m³. Skipet har en slakk tank som er 10 meter bred og 12 meter lang. Det er ballast på tanken.
a) Hvor mye reduseres GM på grunn av denne slakke tanken?
Svar: GG2 = 0,2 m
Oppgave 3. Stabilitetsreduksjon pga fri væskeoverflater
Et skip har et deplasement på 15 520 tonn, et vertikalmoment på 99 301 tm og et FS-moment på 1545 tm. Skipets KM er 7,32 meter.
a) Hvor mye reduseres GM og grunn av den slakke tanken?
Svar: GG2 = 0,099 mb) Hva blir skipets Korrigerte KG?
Svar: KG2 = 6,497 mc) Hva blir skipets korrigerte GM?
Svar: G2M = 0,82 m
Oppgave 4. Stabilitet reduksjon på grunn av fri veskeoverflate på dekk
M/S Linda er lastet til et deplasement på 12000 tonn og GM er 1.4 meter. Det samler seg sjøvann på hoveddekk tilsvarende 8 meter langt og 6 meter bredt. Vannhøyden er ca 1,00 meter.
a) Vis med beregninger og tegn figur.
Svar: KG2 7,57 m, G2M 1,36 mb) Hvordan påvirker dette skipets stabilitet?
c) Hva med virkningen dersom bredden på FS-området var delt i to langskips?
Svar: 144 m4 - 36 m4, G2M = 1,372 md) Beregna GZ-kurven og vis når dekket kommer i vann og når skipet kantrer.
Oppgave 5. Stabilitet reduksjon på grunn av fri veskeoverflate
Vis ved beregning virkningen av fri væskeoverflate på stabiliteten dersom en fyller den ballasttanken som har størst FS og Forepeak tanken. Begge tankene skal være 60% fulle på M/S Sidus.
Gå ut fra at deplasementet på M/S Sidus er 14 000 tonn før fylling og GM er 2.0 meter.
a) Resultatet av beregningene før og etter skal vises på GZ-kurve i to forskjellige farger og G2M etter lasting.
Svar G2M = 0,73 m
Oppgave 6. Fri veskeoverflate
Et skip med deplasement på 5000 tonn har en bunntank i hele skipets bredde. Tanken er 12 meter lang, 16 meter bred og i snitt 1,4 meter høy.
a) Hvor mye påvirker fri væskeflate skipets stabilitet dersom tanken fylles delvis med sjøvann?
Svar: GG2 0.840 m (4096 m4)b) Hva blir virkningen dersom tanken deles med ett tett midtskott (tverrskips)?
Svar: GG2 0.840 m (4096 m4)c) Hva blir virkningen av fri væskeflate i tanken dersom den deles i to langskips?
Svar: GG2 0.21 m (1024 m4d) Hva gir best virkning på stabiliteten, er det å sette inn et langskip- eller tverrskipsskott?
Oppgave 7. Fri veskeoverflate
Et skip har en slakk tank som er 12 meter lang og 9 meter bred. Tanken inneholder bunkers med tetthet på 0,915 tonn/m³. Skipet har et deplasement på 6 785 tonn.
a) Hvor mye reduseres GM på grunn av denne slakke tanken?
Svar: GG2 = 0,098 m
Oppgave 8. Fri veskeoverflate
Et skip har et volumdeplasement på 5 000 m³ og seiler i brakkvann med en tetthet på1,017 tonn/m³. Skipet har en slakk tank som er 10 meter bred og 12 meter lang. Det er ballast på tanken.
a) Hvor mye reduseres GM på grunn av denne slakke tanken.
Svar: GG2 = 0,2 m
Oppgave 9. Fri Veskeoverflate
Et skip har et deplasement på 15 520 tonn, et vertikalmoment på 99 301 tm og et FS-moment på 1 545 tm. Skipets KM er 7,32 meter.
a) Hvor mye reduseres GM og grunn av den slakke tanken?
Svar: GG2 = 0,099 mb) Hva blir skipets korrigerte KG?
Svar: KG2 = 6,497 mc) Hva blir skipets korrigerte GM?
Svar: G2M = 0,82 m
2.1.14. Beskrive virkningen på GM ved fylling/lensing av bunntank, og hensyn å ta
Oppgave 1. Lensing av akterpeak på M/S Sidus
M/S Sidus har et deplasement på 34 364 tonn og skal lense WB akterpeak for å få mindre akterlig trim ved ankomst. GM før lensing er 0,80 m. Akterpeaken er full før du begynner lensning av tanken.
a) Beregna skipets G2M ved 80% fylling?
Svar: 0.386 mb) Beregna skipets G2M ved 50% fylling?
Svar: 0.533 mc) Beregna skipets G2M ved tom akterpeak?
Svar: 0.918 md) Hvorfor blir først stabiliteten verre før den blir bedre?
Se og drøft bilde fra eksamen: FTM02H maskinoffiserutdanning, 2016)
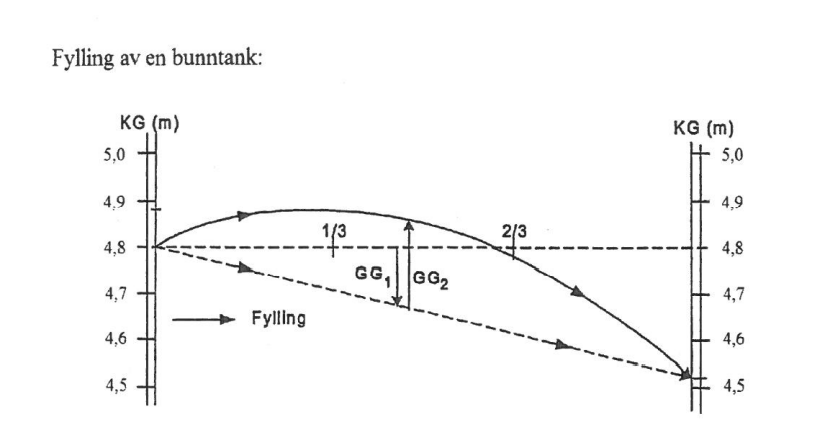
Oppgave 2. Lensing av bunntank på M/S Sidus
M/S Sidus har et deplasement på 49862 tonn og en KG2 på 12,92 meter, det skal lenses WB 1 P og WB 1 S som er lastet til 100%.
a) Beregna skipets G2M ved 80% fylling?
Svar: 0.329 mb) Beregna skipets G2M ved 50% fylling?
Svar: 0.281 mc) Beregna skipets G2M ved tom WB1P/S?
Svar: 0.242 md) Hva er din konklusjon ved lensing av ballast i oppgaven?
Oppgave 3. Fylling av ballast på M/S Sidus
M/S Sidus er lastet til referanse dypgående på 12.00 meter, det er bestemt at hun skal ta in ballast på forepeak tanken. Tanken skal fylles helt opp. G2M før ballasting er på 0,6 meter.
a) Hva blir G2M når tanken halvfull?
Svar: 0.671 mb) Hva blir G2M når tanken er full?
Svar: 0.721 mc) Hvorfor blir stabiliteten bedre med fylling av ballast i forepeak tanken?
2.1.15 Definere dynamisk stabilitet og beregne arealet under GZ-kurven ved Simpsons formel.
Dynamisk stabilitet
En kan bruke uttrykket "momentarbeid" om dynamisk stabilitet. Når en kraft virker på en arm over en gitt vinkel, er det utført et arbeid. Når et skip i opprett tilstand krenges over en viss vinkel, blir det utført et arbeid.
Skipet yter en motstand mot krengningen lik det arbeidet som utføres. Skipet blir tilført energi. Dynamisk stabilitet er definert som den totale krengeenergien som lagres i skipet når det krenges en viss vinkel.
Dynamisk stabilitet
Dynamisk stabilitet nytter man når en vil undersøke et skips bevegelser i bølger, og uttrykker skipets evne til å rette seg opp etter krengning.
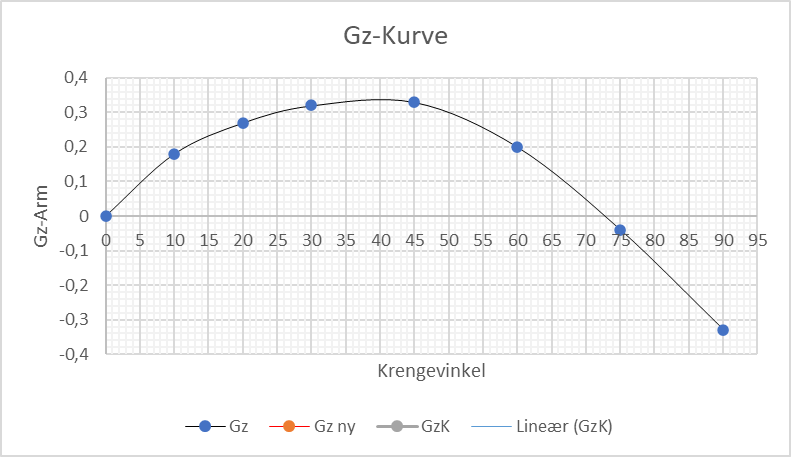
Oppgave 1. Dynamisk stabilitet
Et skip har et deplasement på 5 000 tonn og KG er 5,1 meter. GZ-kurven for skipet er som vist under. KM er 5,7 meter.
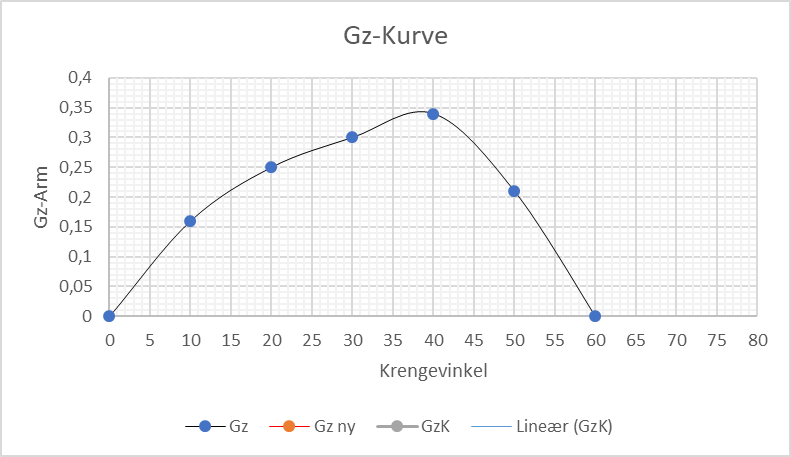
a) Hva blir stabilitetens utstrekning?
Svar: 0 - 60°b) Regn ut dynamisk stabilitet og kontroller alle stabilitetskrav opp mot regelverket?
Svar: 0-30° 0.100 m.rad, 30-40° 0,057 m.rad, 0 - 40° 0,157 m.rad, GM 0,6 m, GZ maks = 37°, GZ 30 = 0,3 m
Oppgave 2. Dynamisk stabilitet
Mercandian Importer har et deplasement på 4115 tonn og en GM på 0,98 meter.
Skipet har følgende GZ-kurve, kan du sjekke om hun følger kravene til stabilitet?
Svar: A 0-30°=0,104 m.rad. A 30-40° = 0,059 m.rad. A 0-40° = 0,163 m.rad
2.1.16 Kontrollere at skipets stabilitet tilfredsstiller stabilitetskravene ved oppslag i forskriftene.
I Sjøfartsdirektoratets "Regler for passasjerskip og lasteskip m.v." 2006, Avsnitt 3.1.2, Kap. 5, "Stabilitet" § 14, er det skrevet følgende:
Intakt stabilitet for skip med bruttotonnasje på 50 og derover
"Intakt stabilitet for skip med bruttotonnasje på 50 og derover":
"Dersom ikke annet er bestemt, skal følgende minimumskrav tilfredsstilles i enhver lastetilstand, jfr. § 15, når krysskurver er beregnet med fri trim:
a) Arealet under kurven for rettende arm (GZ-kurven) skal være:
- minst 0,055 m.rad. regnet opp til en krengevinkel på 30°.
- minst 0,09 m.rad. regnet opp til 40° eller fyllingsvinkelen dersom denne er mindre enn 40°.
I tillegg skal arealet under GZ-kurven mellom krengevinklene 30° og 40°, eller mellom 30° og fyllingsvinkelen dersom denne er mindre enn 40°, være minst 0,03 m.rad.
b) Rettende arm (GZ) skal være minst 0,20 m ved en krengevinkel lik eller større enn 30°
c) Krengevinkelen hvor rettende arm har størst verdi (GZmaks), bør være større enn 30°, og skal aldri være mindre enn 25°.
d) Initialmetasenterhøyden (GM) skal være minst 0,15 m.
e) For passasjerskip skal krengevinkelen ikke overskride 10° når alle passasjerene plasseres i skipets ene side på ugunstigste måte.
I Kap. 8, "Spesielle byggekrav for forsyningsskip og slepebåter", § 43 "Stabilitet" heter det videre:
Stabilitet
a) Arealet under kurven for rettende arm (GZ-kurven) skal være:
- minst 0,070 m.rad. regnet opp til en krengevinkel på 15° når maksimum rettende arm (GZ) opptrer ved 15°
- minst 0,055 m.rad. regnet opp til 30° når maksimum GZ opptrer ved 30° eller mer.
Når maksimum GZ opptrer mellom 15° og 30°, skal arealkravet under GZ-kurven opp til den vinkel hvor maksimum GZ opptrer bestemmes av formelen:
Formel
minimum areal = 0,055 + 0,001· (30° - Ø maks.)
der "Ø maks" er den vinkel hvor GZ-kurven når sitt maksimum.
I tillegg skal arealet under GZ-kurven mellom krengevinklene 30° og 40°, eller mellom 30° og fyllingsvinkelen dersom denne er mindre enn 40°, ikke være mindre enn 0,03 m.rad.
Krengevinkelen
b) Krengevinkelen hvor den rettende arm har størst verdi (GZ-maks), skal aldri være mindre enn 15°.
Fribordet ved akterstevnen
c) Fribordet ved akterstevnen skal aldri være mindre enn 0,005 · L for noen lastetilstand.
Initialmetasenterhøyden (GM)
d) Initialmetasenterhøyden (GM) skal være minst 0,15 m.
2.1.17 Beskrive virkningen av stabiliteten og forholdsregler som må iakttas som følge av:
Lasting/lossing av tunge løft.
Har blitt tatt med i tidligere oppgaver under punk 2. stabilitet.
Forbruk/lensing fra bunntaker.
Har blitt tatt med i tidligere oppgave under punkt 2. stabilitet.
Nedising av overbygg og rigg.
Her vil jeg anbefale å bruke fremføring av skip med navigasjonskontroll av Norvald Kjerstad, Del IV - Is navigasjon.
Følgende algoritmen har blitt utviklet av Overland for å forutse ising på skip som kommer av sjøsprøyt.
Ising på skip som kommer av sjøsprøyt
PPR $= \frac{Va\ (Tf\ -\ Ta)}{1 + 0,3\ (Tw - Tf)}$
PPR = Icing Predictor (Isingsparameter)
Va= Wind Speed/ Vindhastighet (m/s)
Tf = Freezing point seawater (-1.7°C) - (-1,8°C) /Sjøvannets frysepunkt
Ta = Air Temperature/Lufttemperatur (°C)
Tw = Sea Temperature/Sjøtemperatur (°C)

Sjøis har sirka en massetetthet på 0,917 t/m³.
Oppgave med eksempel
Dersom det er vindstyrke på 10 m/s, lufttemperatur på -10°C og sjøvannstemperatur på + 2°C og en forventer at et areal på skipet på 100 m² vil være utsatt for ising.
Hvor mye vil vekten på skipet øke i verste fall de 5 neste timene?
PPR $= \frac{10 m/s\ ( - 1.8\ deg\ C\ -\ - 10deg\ C)}{1 + 0,3\ (2deg\ C - \ - 1,8deg\ C)}$= 38,3
En går inn i tabellen og finner ut at vi har moderat på isparameteret, det vil si at det sannsynlig vil danne seg 0,7 cm til 2 cm is i timen på det utsatte området. Det vil si at etter 5 timer i verste fall har vi 10 cm isdannelse på området.
-
Høyde på isdannelse = 2cm/time x 5 timer = 10 cm = 0,1 meter
-
Vekt = areal x høyde x densitet = 100 m²x 0,1 m x 0,917 t/m³= 9,17 tonn
Detter høres ikke så mye ut, men tenk deg 9,17 tonn på 5 timer på et lite areal, isen kommer som regel på dekk og over, noe som sørger for økt tyngdepunkt.
Oppgave 1
M/S Linda har et AW på sirka 2700 m², tenk deg at 40% av dette arealet er utsatt for isdannelse. Gjennomsnittshøyden på isdannelsen er 13 meter over kjølen. Linda hadde et dypgående på 8,6 meter og en KG2 7,62 meter ved avgang havn. Linda vil bli utsatt for denne type vær i sirka 10 timer før de kommer seg innaskjærs.
Værdata:
- Vindstyrke 18 m/s
- Lufttemperatur -9°C
- Sjøtemperatur 2,3 °C
a) Lag en GZ-kurve for kondisjonen ved avgang.
b) Hvor mye blir vekten av isdannelsen?
Svar: 396.1 tonnc) Hva blir ny G2M etter isdannelsen?
Svar: 0,903 md) Lag ny korrigert GZ-kurve og diskuter forholdene.
e) Hva kan skipet gjøre for å bedre stabiliteten?
Oppgave 2.
M/S Mercandian Importer er på vei til Island og er lastet til WNA, skipet har en G2M på 0,92 meter. Dagen før ankomst skal det blåse opp til nord-vest storm. Sjøvannstemperaturen er målt til 2°C og temperaturen ute er - 12°. Kapteinen forventer bare isdannelse i forkant av midskipskranen, han lurer på hvor stor innvirkning dette vil ha på skipets stabilitet? Og hvilke tiltak en kan gjøre for å bedre stabiliteten?
Vannopptak i dekkslast.
I henholdt til tømmerkoden, punkt 4.1.3 står det at udekket tømmer på dekk kan vekten endres på sjøreisen, mens innpakket tømmer i buntet last ikke endrer seg. Det bør legges særskilt vekt på innvirkningene denne økte vekten kan ha på stabiliteten under reisen. Hvordan vektøkning av tømmerlast skal beregnes finner du i vedlegg C «masseendring av tømmerlast på grunn av vannabsorpsjon».
Dersom en skal beregne massendring (P) av trelast brukes følgende formel:
Massendring (P) av trelast
δP,% = TPl x δPday,%
δP,% = Masseendring av trelast
TPl = Planlagt lengde av sjøreise
δP day = Trelastens masseendring per dag i henholdt til tabell C1.
Oppgave eksempel
Fra St. Petersburg til London, en seilas som tar 5 dager for M/S Mercandian Importer.
Eks 1. Treplanker/sagt tre:
δP,% = TPl x δPday,% = 5 x 0,83 = 4,15
Eks 2. Runde trestokker
δP,% = TPl x δPday,% = 5 x 0,11 = 0,55
Svaret en kommer frem til er masseendring av dekkslasten, dersom en har 100 tonn tømmer på dekk kan en gå utifra at dersom en har plank vil vekten nå være ca 104 tonn ved ankomst London. Dersom en lastet rundstokker i tømmer ville vekten vært ca 100,6 tonn.
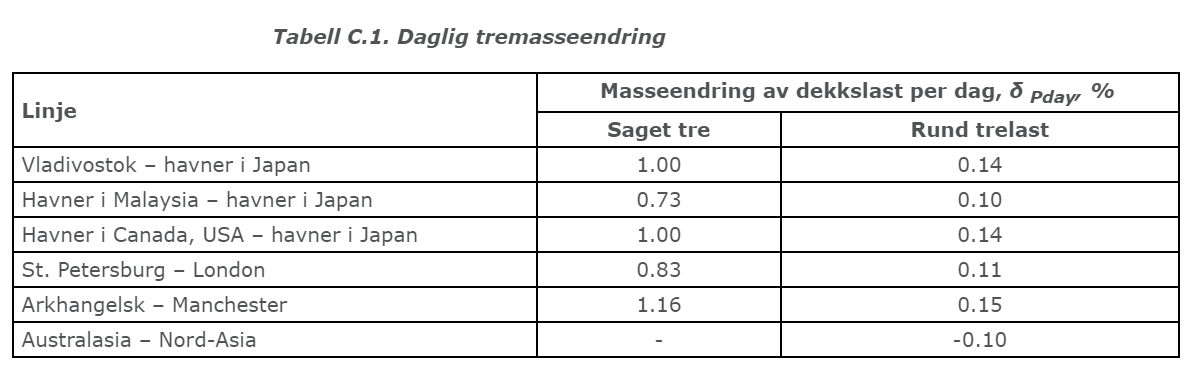
Tabellen C.1 er hentet fra tømmerkoden.
Dersom en får, δP større/eller lik 10% skal en ta med økt vekt av tømmeret med i stabilitets beregningene.
Oppgave 3
Du skal laste tømmer på dekk i Quebec, Canada for Manchester, UK. Distansen er 2903 n. mil, beregnet fart for reisen er 11 knop.
Skipets date før lasting av tømmer på dekk:
- Skipet ligger even keel 4,62 meter
- G2M 1,12 meter før lasting av tømmer i form av sagte treplanker.
- Det er beregnet å ta med 80 tonn tømmer på dekk, lasten vil ha en VCG på 9,3 meter.
a) Gjør en stabilitetsberegning ved avgang for worst kondition.
2.1.18 Være kjent med de spesielle stabilitetsforhold som er knyttet til operasjon av fiskefartøyer og bore-plattformer.
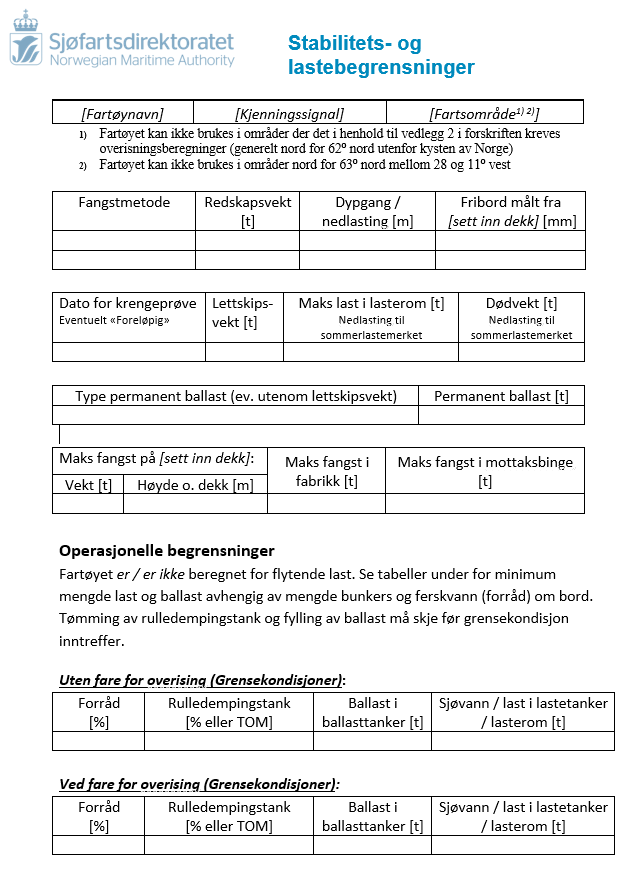
Skjema/bilde ovenfor er hentet fra Sdir.no
Skjema stabilitet og lasteinstruks for fiskefartøy er hentet fra sjøfartsdirektoratet, sjøfartsdirektoratet mener at det er viktig/nyttig å ha et slikt dokument tilgjengelig om bord. Skjema gjelder for fartøy over 15 meter, det oppfordres fra sjøfartsdirektorate at informasjonen sendes inn. Grunnen til utfylling av skjema er at stabilitets- og lasteinstruksen skal være en oppsummering av stabilitetsdokumentasjonen til fartøyet. Stabilitetsdokumentasjonen skal gjøre det oversiktlig for både skipsfører, eier og eventuelt andre som er involverte i skipets stabilitet eller kapasitet beregninger for det gjeldene fartøyet.
Under andre koder på IMO-vege er det utrettet en kode om hvordan en skal beregne stabilitetsplansje for fiskefartøy, koden heter som følgende: Anbefaling om nøyaktighet av stabilitetsinformasjon for fiskefartøy.
Oppgave 1
Gå i den internasjonale koden om intakt stabilitet, 2008, del B
Krav til stabilitet for fiskefartøy:
a) Finn krav til fiskefartøy, dette er et omfattende tema. Prøv å ta med deg så mange punkter som mulig.
Oppgave 2
Bruk den ikke obligatoriske koden: Anbefaling om nøyaktighet av stabilitetsinformasjon for fiskefartøy.
a) Nevn noen anbefalinger som bør være med når en skal utarbeide en stabilitetsplansje til et fiskefartøy.
Hovedfokuset vårt vil være på stabilitetskrava på lovdata, Forskrift om konstruksjon, utstyr og drift av fiskefartøy med lengde 15 meter eller mer, kapittel 3, stabilitet og tilhørende sjødyktighet. Svar på følgende spørsmål fra lovdata.
Oppgave 3
a) Hva er minste kravet til stabilitet for et fiskefartøy på over 24 meter?
b) Hva menes med §3-2.2?
c) Hva menes med permanent ballast?
d) §3-4 Særlige fiskeforhold, hva innebærer dette?
e) Hvilke krav skal et fiskefartøy oppfylle dersom det er utsatt for sterk vind og rulling?
f) § 3-6 Vann på dekk, hvilke stabilitetskrav skal et fiskefartøy oppfylle for å motstå virkningen av vann på dekk?
g) Ifølge § 3-7 Driftstilstand skal fiskefartøy ha noen utregna kondisjon, hva skal disse kondisjonene inneholde?
h) Hvordan skal et fartøy være konstruert som går i område der ising kan forventes?
i) Hvilke stabilitetsopplysninger skal være om bord?
j) Hvilke krav er gjeldene for fiskefartøy over 100 meter i skadet tilstand?
k) Hvilke krav settes til fribord på fiskefartøy?
Oppgave 4
Fiskefartøyet «Elvine» har følgende teknisk data:
- LOA 10,11 m
- Brede 3,6 m
- Dybde i riss 1,60 m
- Byggeår 1991.
For dette fartøyet gjelder følgende regelverk: Forskrift om fiskefartøy med største lengde under 15 meter.
Plansjen til Elvine inneholder følgende intakt kondisjoner:
1: Lettskip,
2: Avg. Havn, 100% på tanker,
3: Ank. Havn, 10% på tankene,
4: På felt, 50% på tanker dk. Last,
5: På felt, 50% på tanker, fullastet,
6: Ank. Havn, 10% på tanker, fullastet.
7: Ank. Havn, 10% på tanker, 20% last.
Krengeprøve og lettskipsdata.
Skrogdatabok som inneholder følgende: Tankdata, hydrostatiske data, kryss kurve, KG-maks. kurve og offset tabeller og plott for skrog, tank og lasterom.
a) Sjekk at fiskefartøyet «Elvine» har alt nødvendig stabilitetsdata om bord i henholdt til regelverket.
Oppgave 5. Stabilitetsforhold boreplattform
Bruk lovdata og se på følgende forskrift og besvar spørsmålene under:
Forskrift om stabilitet, vanntett oppdeling og vanntette/værtette lukningsmidler på flyttbare innretninger
a) Hva sier § 8 angående krengeprøve og lettskipsdata?
b) Hvilke tilstander skal det lages en KG-grenskurve for?
c) Hvilke krav settes til KG-grenskurve i operasjonstilstand?
d) Hva skal være med i de daglige beregninger av lastetilstanden?
e) Hvilke intaktstabilitetskrav er det til boreplattformer?
f) Hva sier kravene til skadestabilitet for boreplattform?
g) Ved antatt skade er det to hovedtyper skade, hvilke skader er dette?
h) Hvor stor skal en gå ut ifra at kollisjonsskaden er på en halvt nedsenkbar innretning?
i) Hva er kravet til fribord på en boreplattform?
2.1.19 Beregne tilnærmet GM av krengeprøve og rulleperiode, og drøfte metodenes begrensninger.
Krengeprøve.
Reglene for krav til krengeprøve finner vi på forskrift om bygging av skip, kapittel 3. Stabilitet § 18 punkt 3.
Krengeprøve er et fysisk eksperiment. Under krengeprøven måles skipets GM i den aktuelle kondisjonen. Hovedmålet med krengeprøven er følgende. Bestemme vertikal plassering av metasentret for lettskip KGwls. Beregne lettskipsvekt WLS og dermed også fartøyets maksimale lasteevne. Krengeprøven foretas under offentlig kontroll. Krengeprøve rapporten er et av fartøyets viktigste dokumenter.
Forberedelse til krengeprøve
Leder sammen med assistenter sørger for at følgende blir gjort før krengeprøven:
- Foreta inspeksjon av tanker og rom.
- Utstyr som ikke tilhører skipet, men som blir værende om bord under krengeprøven må veies og merkes av på arrangement tegning.
- Bestemme massen på krengevekten.
- Bestemme hvor lengde på og plassering av loddsnorene, minst 2 stykk.
- Sørge for at forbindelsen mellom tanker som inneholder væske er stengt dersom mulig.
- Sikre løse vekter.
- Kontroller vekt av krengevekter.
- Fremskaffe værdata.
- Kontakte taubåt dersom nødvendig.
- Kontrollere at kommunikasjonsutstyret fungerer.
- Kontakt sjøfartsmyndighetene.
- Fremskaffe krengerapportskjema fra sjøfartsmyndighetene.
- Sørg for at alt unødvendig utstyr blir tatt på land.
- Kontroller dypgående ved kai og sørg for at du har nok dypgående.
Utførelse av krengeprøve
- Notere sted, dato, tidspunkt, temperatur og værforhold.
- Kontrollere at fortøyningene er slakke.
- Kontrollere at fartøyet flyter uten krengning, ta et draft survey.
- Måle temperaturen på sjøvannet.
- Ta prøver av sjøvannet for å bestemme massetettheten (densiteten).
- Lese av skipets dypgang.
- Flytting av krengevekten, det skal være 8 avlesninger. Dette grunnet «Tilfeldig feil». Då må vi bruke midling som vil redusere eventuelle systematiske feil og feil på utstyret.
- Krengning 2 - 4 °.
Beregning av Wls og KGwls. Korrigering for fremmede vekter.
Beregning
Wls = ∆ - ∑mi
∑mi = summen av alle fremmede vekter, Wls = vekt lett skip og ∆ = er vektdeplasement fra hydrostatiske data, tatt etter draft surveyen.
Korreksjon for EFVO (EFVO = Effekt fri veskeoverflate).
GG'
Beregning av KG under krengeprøven.
KG = KM - G'M - GG'
Beregning av KGwls
∆ x KG = Wls x KGwls + ∑Xi x mi
∑ Xi= felles KG for alle løse lastene (fremmede vekter).
Oppgave 1. Krengeprøve for stabilitetskontroll
Et spesialbygget skip har følgende data:
Skipets dødvekt............................. 3500 tonn
Bredde............................................. 12.57 m
Lengde............................................ 85.04 m
Dybde i riss....................................... 8.50 m
Midlere dypgående lastet.............. 7.38 m
CB lastet............................................ 0.742
KM lastet.......................................... 8.35 m
Før avgang ønsker man å foreta en krengeprøve for å bestemme skipets endelige stabilitet og tar om bord en vekt på 10 tonn som blir plassert med tyngdepunkt 0.5 m over dekk og 5.75 m fra senterlinje. En 7 m lang loddsnor fikk et utslag på 0.15 m. Etterpå ble vekten losset igjen. Ingen slakke tanker under krengeprøven.
a) Beregne skipets deplasement?
Svar: ∆ = 6000 tonnb) Beregne GM og KG lastet skip.
Svar: GM = 0,447 m & KG 7,903 m
I Code of Safe Practice for Ships Carrying Timber Deck Cargoes, 1991 (Tømmerkoden) står det følgende i Appendix B, punkt 5, During the voyage.
«The ship's heeling angle and rolling period should be checked, in a seaway, on a regular basis;»
Oppgave 2. Stabilitet ved rulleperiode
Et skip har følgende data:
Lpp........................... 70.00 m
Bredde..................... 13.00 m
Dypgang..................... 4.50 m
CB lastet ................... 0.70
F (konstant)................ 0.80
Man ønsker å kontrollere skipets stabilitet ved hjelp av rulleperioden.
Fortøyningene er helt slakke og det er vindstille uten strøm. Skipet settes i bevegelse ved å flytte et hiv fra side til side og gjennomsnittlig rulleperiode måles til 12.5 sek.
a) Beregne skipets deplasement?
∆ = 2938,2 tonnb) Finn GM i lastet kondisjon?
GM = 0,692 m
Oppgave 3. Følgende data er gitt:
Skipets dødvekt........ 2200 tonn
LPP.............................. 69 meter
Bredde......................... 12,85 meter
Dypgang. Lastet............. 4,75 meter
CB ...................................... 0,78
F (konstant)....................... 0,80
KM lastet............................ 5,05 m
Rulleperiode gjennomsnittlig måles til 15 sek.
Følgende GZ - verdier gjelder for skip i lastet kondisjon:
GZ - verdier for skip i lastet kondisjon
v/10° = 0,08 m, v/20° = 0,16 m, v/30° = 0,24 m, v/45° = 0,30 m, v/60° = 0,18 m
a) Beregn skipets deplasement lastet og lettskip.
Svar: 3367 tonn/1167 tonnb) Finn skipets GM og KG i lastet kondisjon.
Svar: 0,47 m/4,58 mc) Tegn skipets GZ-kurve og indiker på kurven hvor skipet har størst opprettende moment.
Svar: v/45°
Oppgave 4. Krengeprøve
Et skip har et deplasement på 20 000 tonn og KM på 8 meter. Stabilitet skal kontrolleres ved en krengeprøve. En kontainer på 20 tonn blir flyttet en avstand på 15 meter fra babord side til styrbord side. En loddsnor på 12 meter er hengt opp i masta og loddsnoren gir et utslag på 0,65 meter.
a) Hva blir skipets GM og KG?
Svar: GM = 0,277 m & KG = 7,723 m
Oppgave 5. Krengeprøve
Et skip har et deplasement på 35 200 tonn. Stabilitet skal kontrolleres ved hjelp av en krengeprøve. En loddsnor på 20 meter blir hengt opp. To vekter på 40 tonn hver er blitt tatt om bord og plassert på hver side av skipet. Vektenes høyde over kjølen er 16 meter. Deretter blir den ene vekten flyttet over på motsatt side, en avstand på 20 meter. Loddsnora gjør et utslag på 0,45 meter. KM etter vekten er tatt om bord er 11,25 meter.
a) Hva blir GM og KG?
Svar: GM 1,01 m, KG 10,24 mb) Hva blir GM og KG etter at vekten er tatt i land, når KM nå leses av til 11,30 meter?
KG LS = 10,227 m GM LS = 1,073 m
Oppgave 6. Rulleperiode
Et skip kommer ut for meget dårlig vær og ønsker å kontrollere stabiliteten ved hjelp av en rulleperiode. Etter en gjennomsnittsmåling blir rulleperioden satt til 20 sekunder, skipets bredde er 9 meter.
a) Hva blir skipets GM?
Svar: 0,129 mb) Er skipet sjødyktig med slik GM?
Oppgave 7. Rulleperiode
Et skip skal ut i dårlig vær og kapteinen lurer på om du kan finne rulleperioden, GM er 2 meter og skipets bredde er 18 meter.
a) Hva blir skipets rulleperiode?
Svar: 10.18 sek
Oppgave 8. Rulleperiode
Et skip kommer ut for meget dårlig vær og ønsket å kontrollere stabiliteten ved hjelp av en rulleperiode. Etter en gjennomsnittsmåling blir rulleperioden satt til 10 sekunder, skipets bredde er 9 meter.
a) Hva blir skipets GM?
Svar: GM 0,5184 mb) Er skipet sjødyktig med slik GM?
Svar: Ja
Oppgave 9. Rulleperiode
Et skip skal ut i dårlig vær og kapteinen lurer på om du kan finne rulleperioden, GM er 2 meter og skipets bredde er 18 meter.
a) Hva blir skipets rulleperiode?
Svar: 10.18 sekund
Oppgave 10. Rulleperiode
1. M/S Linda har en GM 0.3 meter.
Hva blir skipets rulleperiode?
Svar: 29,8 sekund
2. M/S Linda har en GM 1.2 meter
Hva blir skipets rulleperiode?
Svar: 14.9 sekunda) Drøft forskjellen på rulleperioden, når Linda har GM på 0.3 meter mot GM 1.2 meter.
2.1.20 Laste/losse/Ballaste skipet til ønsket stabilitet uttrykt ved gitt GM, KG eller ønsket GZ ved 30 grader krengning:
øKG = (KY(KN)- øGZ)/sin30⁰ & øGM = (øGZ-MoS)/sin30⁰.
Oppgave 1. Ønsket GM på M/S Linda.
På M/S Linda gjenstår det å laste dekkslast, skipet er lastet til et deplasement på 21 030 tonn.
- Før restlast var skipets GM beregnet til 0,32 m. Det skal tas om bord så mye restlast som mulig, men kapteinen ønsker å ha en GM på minimum 0,30 meter og at du ikke overstiger sommermerket.
- Dekkslastens VCG er beregnet til 12,5 meter, vi skal fordele lasten mellom dekke og ballasttankene Nedre W/T No 5 P/S.
a) Hvor mye kan vi laste for å beholde en GM 0,30 meter?
Svar: Dekk 323 tonn/ballast 88 tonnb) Hva blir påvirkningen av FS -moment?
Svar: 0.004 m
Oppgave 2. Lastes til ønsket GZ
M/S Linda ligger i havn og har lastet til et deplasement på 18920 tonn og skal laste til sommermerket.
- KG er beregnet til 7,80 meter.
- Resten av ledig dødvekt skal brukes til dekkslast og eventuelt som ballast i dobbelbunntank nr. 1, 2, 3 og 4. Tankene må fylles helt opp dersom de skal brukes.
- Midlere VCG for dekkslasten blir beregnet til 14,50 m, og LCG fra AP blir regnet til 76,00 m.
a) Hvilken KG må skipet laste til for å få en effektiv GZ-arm på 0,461 m ved 30⁰?
Svar: 7,80 mb) Hvor mye dekkslast kan skipet ta maksimalt for å tilfredsstille GZ-armen ved avgang?
Svar: 1176,2 t når vi legger ballasten på DB 3&4c) Beregn og tegn GZ-kurven og kontrollere opp mot gjeldene regelverk, se punkt (2.1.16).
Oppgave 3. Ønsket GZ
M/S Mercandian Importer ankommer Trondheim (N 63°25' E 010°23') for bunkring og utnyttelse av eventuelt ledig deplasement kapasitet til tømmer på dekk. Etter skipet er ferdig lastet i Trondheim, skal det videre til Reykjavik på Island (N 64°09' W 021°56').
- Skipets fart regnes til 12 knop, og det totale forbruket til 12 tonn per døgn.
- Distanse fra Trondheim til E/W 000° er på 336 n.mil.
- Skipets deplasement ved ankomst Trondheim er på 3897,0 tonn, med tilhørende VCG = 4,60 m og FS-mom. = 108,9 tm.
- Det skal bunkres 57,0 tonn Fuel Oil, I FO tk nr. 4 P/S.
- Avgang Trondheim er satt til kl. 1400 den 8.desember.
Eventuell ledig deplasementskapasitet etter bunkring, vil benyttes til lasting av tømmer på dekk.
a) Hva er største felles vcg dekkslasten kan ha, når man vil forsikre seg om at man ikke overstiger en GZv/30° på 0,30 m ved avgang?
Svar: vcg dekkslast 14,21 m
2.1.21 Sammensatte oppgaver på stabilitet samt retting av dypgående.
Oppgave 1. Beregne dypgående M/S Sidus (T referanse/plansje/dref og T avlest)
Dref/Tref = T skala = T plansje
a) Hva er skala dypgående når avles er Tf 7.45 m T¤ 8.39 m Ta 9.49 m?
Svar: Dref 8.3556 mb) Hva er skala dypgående når avles er Tf 6.85 m T¤ 8.39 m Ta 9.99 m?
Svar: Dref 8.3144 mc) Hva er skala dypgående når avles er Tf 8.45 m T¤ 8.00 m Ta 7.49 m?
Svar: Dref 7.998 md) T skala er 8.25 m, trimmen er 3 meter akterlig. Hva er avlest dypgående?
(Svar: Tf 6.842 m T¤ 8.333 m Ta 9.833 m)e) T skala er 10.20 m, trimmen er 1 meter forlig. Hva er avlest dypgående?
(Svar: Tf 10.719 m T¤ 10.222 m Ta 9.722 m)f) T skale er sommer merket, trimmen er 1.23 meter akterlig. Hva er avlest dypgående?
(Svar: Tf 11,419 m T¤12,031 m da12,646 m).
Oppgave 2. Beregne dypgående M/S Mercandian Importer
(Tref og T avlest)
a) Hva er skala dypgående når avlest er Tf 2.28 m T¤ 3.30 m Ta 4.31 m?
Svar: 3.28 mb) Hva er skala dypgående når avles er Tf 4.45 m T¤ 4.00 m Ta 3.49 m?
Svar: 3,99 mc) T skala er 4.12 m, trim er 2.02 meter akterlig. Hva er avlest dypgående?
Svar: df 3.098 m d¤ 4.109 m da 5.119 m
Oppgave 3. Hva er deplasement og hvor mye hogg eller sagg har M/S Sidus?
a) Dypgang avlest Tf 7,00 m, T¤ 7,56 m og Ta 8,00 m
Svar: 0.0615 m sagg/∆ 31160 tb) Dypgang avlest Tf 8,00 m, T¤ 7,38 m og Ta 7,00 m
Svar: 0.1215 m Hogg/∆ 30615 tc) Dypgang avlest Tf 10,98 m, T¤ 10,63 m og Ta 9,98 m
Svar: 0.1485 m Sagg/∆ 50694 t
Oppgave 4. Fra Tref til avlest, når vi tar med hogg eller sagg.
a) M/S Sidus Tref 9 m skipet har 40 cm trim akterlig og sagg på 15 cm. Hva er avlest dypgående?
Svar: df 8.711 m d¤ 9.06 m da 9.11 mb) M/S Sidus Tref 12 m skipet har 1,5 meter trim akterlig, hogg på 12 cm. Hva er avlest dypgående?
Svar: df 11.318 m d¤ 11,944 m da 12.814 mc) M/S Sidus har avlest dypgående på Tf 7.939 m Ta 8.084 m og sagg på 0.15 meter hva er TRef?
Svar: 8,0921 md) M/S Sidus har avlest dypgående på Tf 5.00 m Ta 6.40 m og hogg på 10 cm hva er TRef?
Svar: 5,5652 m
Oppgave 5. Stabilitet M/S Sidus slakke tanker og GZ-kurve.
Du har et avlest dypgående på Tf 7.95 m T¤ 8.20 m Ta 8.47 m. Skipets KG er beregnet til 9.69 m og vi har et samlet FS-mom på 2800 tm grunnet slakke tanker.
a) Hva er skala dypgående?
TRef = 8,175 mb) Hva er G2M før lossing og lasting av ballast?
Svar: 3.818 m
Du skal losse rom 1 og 2 som er fulle med bomull (bales) som stuer 1.8 m³/t.
Følgende ballast skal lastes:
- Forepeak 60% full.
- WB 2P og WB 2S til 98% full.
c) Hva blir ny G2M etter lossing og ballasting?
Svar: 4.871 md) Tegne GZ-kurve?
Oppgave 6. Stabilitet, bulk og kontainer med M/S SIDUS.
M/S Sidus ligger i Oslo i juni og skal laste for Barcelona. Før lasting har vi inne 100% List of storres departure. Alle rom skal lastes opp med korn i sekk (Bales) som stuer 1.58 m³/t. Det skal lastes 10 (TEU) kontainere i BAY 01 med egenvekt på 12 tonnes hver.
a) Gjør en fullstendig stabilitetskontroll og se at M/S Sidus overholder alle kravene til stabilitet.
Svar: G2M=1.417 m, GZ30°=1.097 m, GZmax = 44°, Areal 0-30=0,242 m.rad. Areal 30-40=0,226 m.rad. Areal 0-40=0,468 m.rad
Avstand Oslo Barcelona 2000 n.mil. Vi regne med at bunkersforbruker tas fra HFO tank 21P/S. Ved ankomst Barcelona skal rom 3 og 7 losses.
b) Hva er ny G2M etter lossing i Barcelona?
Svar: 1,204 m
Oppgave 7. Stabilitet M/S Mercandian Importer
M/S Mercandian Importer ankommer Haugesund med følgende avlest dypgående.
- Tf 3.35 m T¤ 3.23 m Ta 3.05 m.
- I Haugesund skal TD 1 & TD 2 lastes fulle med stykkgods last som stuer 1,20 m³/t.
- Og en kontainer på 20 tonn på Tier 12 Bay 03.
-
FS- mom før bunkring er 165 tm.
-
I tillegg skal det bunkres HFO 60 tonn på Fuel oil tank No 4 P/S.
- KG beregnet til 3.75 m før lasting.
a) Hva er Tref før lasting?
Svar: 3.223 mb) Hvor mye last skal det lastet i hvert rom?
Svar: 691,6 t & 718,3 tc) Hva blir KG2 etter lasting?
Svar: 4,491 md) Hva blir G2M etter lasting?
Svar: 0.909 m
Etter lasting har skipet akterlig trim på 30 cm og sagg på 6 cm.
e) Hva blir avlest dypgående etter lasting?
Svar: df 4,954 m d¤ 5,164 m da 5,254 m
Oppgave 8. Stabilitet M/S Mercandian Importer
M/S Mercandian Importer ligger og laster i en havn i midten av juli. Det er saltvann (1,025 t/m³) i havnen.
Skipet har inne før lasting 180 tonn bunkersolje og 61,9 tonn ferskvann. 22 tonn med proviant/stores og lub-oil tanken er full. Dette gir et vertikalmoment på 322,5 tm.
Fuel-oil tank # 7 er slakk, og FS-mom for denne tanken er ikke tatt med i beregningene.
Skipet skal laste full med last i underrommene av bulk med stuingsfakter på 1,32 m³/tonn.
Skipet skal laste full med last i mellomdekkene med stykkgods av stuingsfaktor på 1,16 m³/tonn. Lukene skal være tomme. Til slutt skal det tas med 4 kontainere (TEU) som plasseres på dekk. Hver av disse kontainerne veier 6 tonn. Vi regner med at kontainerne vil få en VCG på 9,53 m.
a) Finn skipets avgangskondisjon med hensyn til regelkravene for stabilitet?
Svar: GM 0.986 m, GZ 30° 0.385 m, GZmaks 43°, A 0-30° 0.121 mrad, A 30-40° 0.071 mrad, A 0-40° 0,192 mradb) Vis med beregning at dekket tåler belastningen av en kontainer (TEU) på 6 tonn.
Svar: 1,5 t/m²>0,38 t/m²
Oppgave 9. M/S Sidus ligger i New Orleans i juni og skal laste.
Avlest dypgående df 7.50 m d¤ 8.24 m da 8.90 m ved kai i New Orleans.
Du skal laste resterende 4000 tonnes med last i rom 1 og 10. Restlasten er Bulk (Grain) som stuer 1.35 m³/t. KG er beregnet før lasting til 10.57 m. Det totale FS-mom 1820 tm før lasting.
Last først opp rom 10 så resterende last i rom 1.
a) Hva er skala dypgående før lasting?
Svar: 8.178 m ≈8.18 mb) Regn ut full stabilitetsoppgave i henholdt til krava for stabilitet?
Svar: G2M - 2.461 m, GZ 30° - 1.856 m, A0-30° - 0.422 m.rad, A30-40° - 0,380 m.rad, A0-40° - 0,802 m.rad.
Oppgave 10. M/S Linda stabilitet og lasting til sommer sone
M/S Linda ligger i sommersone og skal ta om bord så mye last som mulig. Før lasting hadde M/S Lindas følgende deplasement, beregnet KG og FS -moment:
- ∆ 6028 tonn.
- KG 8.19 meter.
- FS - moment 986 tm.
Følgende last skal lastes:
- Rom 1, 3, & 5 skal lastes fulle med stykkgodsas som stuer 1.86 m³/t.
- Rom 2, 4 & 6 skal lastes med bulk last som stuer 0.75 m³/t. Full opp rom 4, deretter fordel restlasten likt mellom rom 2 og 6. (PS: ikke last over sommer merke).
a) Hvor mye kan skipet laste før det er på sommermerket?
Svar: 15413 tonnb) Oppfyller M/S Linda alle stabilitetskravene?
Svar: G2M - 1,741 m
Linda har 1 meter akterlig trim etter lasting.
c) Hva er Lindas avlest dypgående ferdig lastet?
Svar: df 8.461 m, d¤8.961 m, da 9.61 m
Oppgave 11. Full stabilitets beregning med M/S Mercandian Importer
M/S Mercandian Importer har følgende avlest dypgående Tf 2,85 m T¤ 3,21 m Ta 3,65 m.
Det gjenstår å laste TD 1 og TD 2 med pallelast som stuer 1,86 m³/t, samt to konteinere på 20 tonn som har en vcg på 9,6 m (disse konteineren plasseres på dekk).
Før lasting er KG beregnet til 4.71 meter og det er et FS -mom 251 tm.
a) Hva er skipets ∆ før lasting?
Svar: 2126 tb) Hva er skipets G2M før lasting?
Svar: G2M 0,7469 mc) Hvor mange tonn går det i hvert lasterom (TD 1 og TD 2)?
Svar: 446,2 t/463,4 td) Hva blir deplasementet og G2M etter lasting?
Svar: 0,216 me) Lag en GZ-kurve og fin GZ v/30°og GZ-maks?
Svar: GZ v/30°-0,273 m, GZ-maks 38°
2.2 Krengning
2.2.1. Beregne krengemoment og krengearmen (TCG) av usymmetriske vektfordeling og beskrive at skipet krenger inntil den rettende arm (GZ) = krengearmen.
- Krengearm (krengemoment) = Vekt x Arm (Tcg)
- Rettende moment = Rettendearm (GZ) x deplasement (∆)
Skipet vil krenge til skipet har utlignet kraften påført av krengemomentet. Skipet vil stoppe krengningen når krengemomentet er likt det rettende moment (dynamisk stabilitet).
Eks: På beregning av krengemoment og krengearm M/S Mercandian Importer
Det skal tas et tungløft på M/S Mercandian Importer, men før løfte skal tas velger styrmannen å fylle ballast på motsatt side av der løfte skal tas. Du skal fylle ballast på ballasttank No. 3 P og 5 P helt fulle for å unngå «FS-mom».
Deplasementet før ballasting var 3600 tonn og KG 4,6 meter.
a) Hva blir det krengende moment etter ballasting?
Svar: Krengende moment = Ballast x 4,4 m = (78,9 t + 69,1 t) x 4,4 m = 651,2 tmb) Hva blir krengningen og det rettende moment? (bruk GZ-kurve)
*NB: ser i ettertid at oppgaven har blitt beregnet ut ifra at en fyller tankene fulle, skal egentlig dele tankenes volum på to dersom man skal fylle styrbord eller babord side av tanken, da plansjen viser både styrbord og babord tank i et (sammenslått). Dette gjelder kun for M/S Mercandian Importer plansjen.

KG$\ = \ \frac{16666\ tm}{3748\ t}$ = 4,447 m GM = KM - KG = 5,430 m - 4,447 m = 0,983 m
TCG $= \frac{651,2\ tm}{3748\ t}$ = 0,1737 m (TCG er hvor mye G'en tyngdepunktet trekker seg utfra senterlinjen).

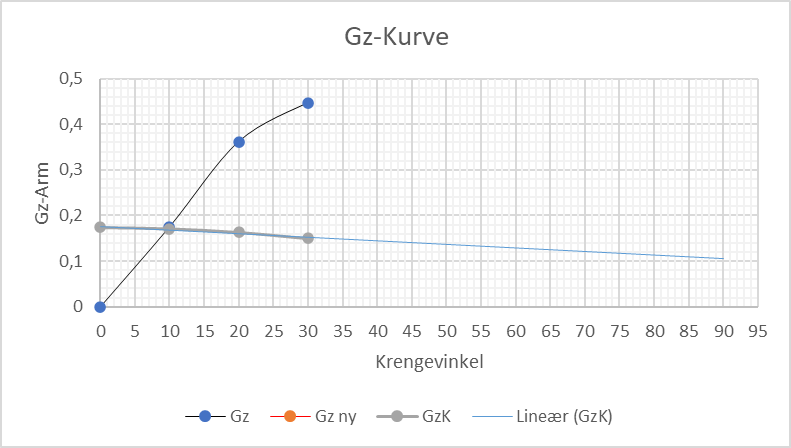
Her ser vi at GzK krysser GZ-kurven ved ca 9,5 grader. Dette gir oss en GZ-arm ved 9,5° på 0,173 m
- Rettende moment = ∆ x GZ -arm = 3748 t x 0,1730 m = 648,4 tm
Som betyr at rettende moment = krengende moment
Oppgave 1. Beregning av krengemoment og krengearm på M/S Sidus
M/S Sidus skal ta et tungløft, det ønskes fra kapteinen at det kompensere for noe av denne krengningen. Han foreslår at du kan fyller opp ballasttanken WB 2 P. Deplasementet før fyllingen begynte er 42848 tonn og en KG på 11,23 meter.
a) Hva blir skipets TCG eller fylling av ballasten?
Svar: 0.0882 mb) Hvor mye krenger skipet?
Svar: 2,38°
Oppgave 2. Beregning av krengemoment og krengearm på M/S Mercandian Importer
M/S Mercandian Importer ligger med babord side til kai og er ferdig utlosset i Rotterdam. Kaien før losset hun med styrbord side til. Da de ankom første kaien hadde MI en litt høy fart, det er nå mistanke om skade ved styrbord side midtskips rett over slagplaten.
Kapteinen tror at skaden best kan inspiseres uten dykker, da det er dårlig sikt i sjøen og samt sterk strøm. For at skipet skal kunne inspiseres må det krenges 12 - 15°.
Før operasjonen skal begynne har du følgende data:
- ∆ 1600 tonn
- G2M 0,9 meter
- TCG 0,05 m (port)
Kapteinen vil at du skal fylle opp ballast tank No. 3 og 5 port
a) Hva blir skipets TCG etter ballasten er tatt om bord?
Svar: 0.2425 mb) Hvor stor krengning vil dette gi skipet?
Svar: 13,67°c) Vis med GZ-kurve hvor stor krengningen blir.
Oppgave 3. Beregne krengemoment på M/S Linda
M/S Linda har fått noe inn i det øvre sjøvannsinntaket på styrbord side, skipet ligger til ankers. Kapteinen ønsker å krenge skipet, han tror at 10 graders krengning til babord vil være tilstrekkelig for å få inspisere eller eventuelt gjøre rent sjøvannsinntaket fra utsiden med MOB-båten. Lindas deplasement er på 15 900 tonn og KG2 = 7,90 m.
Ballasttankene om bord er slakke, så det skal kun transferes ballast slik at vi får en krengning på 10°, da kapteinen tror dette er tilstrekkelig. Vi går ut ifra at det er liten eller ingen endring i skipets G2M. Ballast tankene som skal brukes har en tcg på 8,7 meter
a) Hvor mye ballast må vi transfere fra øvrevingtank No 3 S til øvrevingtank No 3 P?
Svar: 98,29 tonnb) Hva er skipets TCG og krengemoment etter transferingen?
Svar: 0,1076 m/1710.2 tmc) Hva blir skipets dypgående midtskips på babord og styrbord etter transfering, vi går ut ifra at vi lå even keel og uten list før transfering?
Svar: dp 8.58 m/ds 5.24 m
Oppgave 4. Hendelse: Notat fra skipets dekksdagbok M/S Mecandian Importer:
Ankomst Terminalen Delta med avlest dypgående Tf 5,51 m og Ta 5,40 m. Seltgehalt/densitet var tatt av sjøvannet ved terminal og målt til 1,025 t/m³. GM ved ankomst beregnet til 0.80 m. Klokken 14:02 ferdig fortøyd styrbord side til kai. Loddskudd foretatt midtskips, målt til 0,45 m under kjøl. Kun ballast på FP (Fore Peak) som var helt full, det slippes ballast fra FP til ballasttank 3 P slik at skipet ligger even keel og babord list.
Hendelsesforløp:
Kl. 14:30 ankommer lastebil med kontainer, sjåføren beslutter å plassere kontaineren 3 meter inne på kaien til tross for at skipet mannskapet ønsket den plassert mye nærmere. Det var anslått at det var 3 m i fra skutesiden til nærmeste sidevegg på kontaineren, den ble plassert i samme lengderetning som skipet, vekt av kontainer var oppgitt til å være 26 tonnes, bredde av kontaineren er 2,44 meter og med tyngdepunkt i senter. Skipet brukte sin egen kran midtskips til å foreta løftet, SWL = 30 tonnes, på dekk under operasjonen var overstyrmannen og to av dekksbesetningen, hvor en av dem opererte kranen.
a) Foreta beregninger og kom til en konklusjon.
Svar: Dypgående ved løfte m, p.g.a krengning maks dypgående ved kai
2.2.2 Ta krengevinkel av GZ-kurven og beregne omtrentlig krengning av formelen: tan Ø = TCG/GM.
Oppgave 1. Ta krengevinkel, GM og TCG ut av GZ-kurve
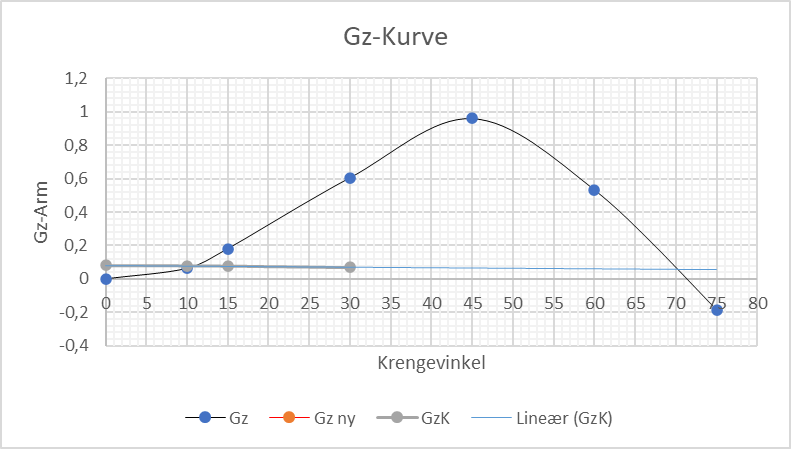
a) Finn kreng vinkelen ut ifra GZ-kurven.
Svar: 10°b) Finn G2M på GZ-kurven.
Svar: 0,40 mc) Bruk GM og TCG, for å finn krengning ved hjelp av formel.
Svar: TCG 0,08/11,31°
Oppgave 2. Ta krengevinkel, GM og TCG ut av GZ-kurve
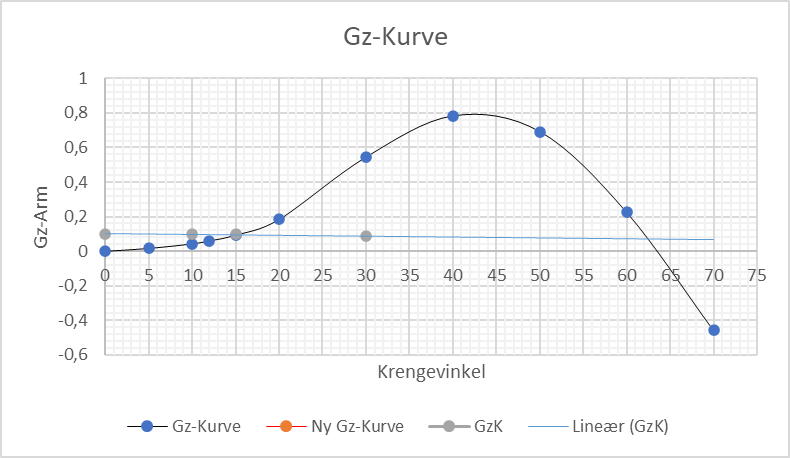
a) Finn kreng vinkelen ut ifra GZ-kurven.
Svar: 15°b) Finn GM på GZ-kurven. G2M 0.32 m
c) Bruk GM og TCG, for å finn krengning ved hjelp av formel.
Svar: TCG 0,1 m/17.35°
2.2.3. Beskrive faremomenter ved lastforskyving og de forholdsregler som må iakttas for å unngå dette.
Faremomenter med lasteforskyvning kan være skader på skip, mannskap, miljø, forskyvning av last og tyngdepunkt, faller over bord, osv.
Dersom lasten forskyver seg tverrskips, har dette en påvirkning på stabiliteten på like linje med oppgavene under punkt 2.2.1. En har mistet stabiliteten opp til det krengende punktet til den siden skipe krenger.
Forholdsregler som må iakttas for å hindre lasteforskyvning er å følge skipets «CARGO SECURING MANUAL» (CSM), se K 12 kapittel 6. Dersom en skal lage en CSM skal punktene nevnt i CSS Code «CODE OF SAFE PRACTICE FOR CARGO STOWAGE AND SECURING» i annex 14 følges. Dersom lasten har forskjøvet seg skal en følge kapittel 7 i CSS coden «Actions which may be taken once cargo has shifted».
Oppgave 1. Lasteforskyvning på M/S Mercandian Importer
M/S Mercandian Importer ankommer Bergen med 5° slagside til styrbord. Dette skyldes at lasten på mellomdekket har forskjøvet seg, NO 3 BB ble fylt opp for å redusere slagsiden til 5°. Tcg for denne tanken er 4,00 meter.
Vekten av forskjøvet last er beregnet til 350 tonn. KG før uhellet inntraff var beregnet til 4,30 meter og deplasementet var 3500 tonn.
a) Hvor langt hadde lasten forskjøvet seg tverrskips retning?
Svar: 1.43 meter
Oppgave 2. Lasteforskyvning på M/S Mercandian Importer
M/S «Mercandian Importer» er ute i meget dårlig vær på en reise fra London til Reykjavik og surringene har begynt å løsne på lasten som ligger på mellomdekket, de har kalkulert med at risikoen er for stor å sette på flere stropper, dersom ikke høgst nødvendig for skipets stabilitet. Du har fått i oppgave å beregne om stabiliteten er tilfredsstillende dersom lasten løsner helt og legger seg i en av siden på tween dekket. Ifølge kapteinen er lasten vekt beregnet til 70 tonn og en forventer en maks forskyvning på 4 meter. Skipets KG2 er 4,87 meter og deplasementet er beregnet til 3937 tonn.
a) Hva blir skipets krengning dersom surringene løsner?
Svar: 6.57°
b) Lag en GZ-kurve med denne krengningen og drøft stabiliteten.
6 timer seinere ligger skipet med krengning og lasten ligger til styrbord side, du er i Nord Atlanteren og det er januar måned. Været har bedret seg, lasten sures fast på nytt. Kan vi rette opp skipet før vi ankommer Reykjavik.
c) Hvor mye ballast må du fylle på WB 3 P & 5 P for å rette opp skipet?
Svar: 63,6 tonnd) Hva blir ny G2M etter fyllingen?
Svar: 0.678 m > 0.15 m
Oppgave 3. Teori i henholdt til Kapittel 6, K 12 Koder og regelverk
a) Hva er CSS koden og hvorfor har vi den?
b) Fortell kort om hva den omhandler?
c) Hva er en lastesikringsmanual?
d) Hvilke skip skal ha en lastesikringsmanual?
e) Hva skal en lastesikringsmanual innhold av informasjon i henholdt til CSS koden?
f) I K 12 er det et utdrag av M/S Sidus sin CSM (Cargo Securing Manual). Hvordan skal du sikre konteinere under dekk i henholdt til M/S Sidus sin CSM?
Sikring av last
Vi vil gå mer inn på sikring av last i punkt 6. Sikring og behandling av last.
Oppgave 4. Krengning M/S Linda
M/S Linda har last i rommene som forskyver seg og skipet krenger 8 ° til styrbord. Kondisjon er som følgende: Deplasement 12000 tonn og GM 1,00 meter.
a) Hvor stort er det krengende moment?
Svar: 1686 tmb) Dersom du fyller øvre vingtank No 4 P med en tcg 9 meter, vil det da være tilstrekkelig for å rette opp slagsiden?
Svar: Ja, du må fylle 187,4 tonn for å ligge uten list.c) Hvor mye ballast måtte du flyttet mellom vingtank 4 styrbord og 4 babord?
Svar: 93,7 tonnd) Hvorfor trenger du bare flytte halvparten av mengden du må fylle?
2.2.4. Beregne krengearm av tverrskipsmomentene om senterlinjen: TCG1 = Σ T.M./∆
Oppgave 1 - lasteforskyvning.
M/S Mercandian Importer er på vei til Haugesund og har vært ute i dårlig vær. Noe av lasten som er lastet på mellomdekket har forskjøvet seg, lastens vekt er beregnet til 50 tonn. Deplasementet før ankomst er beregnet til 3182 tonn og G2M før lasten forskjøv seg var 0,92 meter. Skipet lå uten krengning før lasten forskjøv seg. Vi går utfra at lasten har flyttet seg 3 meter til styrbord.
a) Hva blir krengearmen?
Svar: 0,047 m
Oppgave 2. Krengning med lossing
M/S Sidus skal losse konteinere, kranen på land er i stykker og de har fått inn mobilkraner for å hjelpe til med lossingen. Grunnet lengden på kranene kan de kun losse Row'ene på styrbord side før skipet skal turnes rund å losse Row'ene på babord side. Det er kun Tier 82 som har konteinere, den er full. Skipet ligger uten list og har et deplasement på 42868 tonn. Felles Tcg på konteinerne som er på styrbord side er beregnet til 6,2 meter og vekten per konteiner er beregnet til 9 tonn. GM før lossing er beregnet til 0,90 meter.
a) Hva blir krengearmen og ny GM etter lossing?
Svar: 0,13 m/1,128 mb) Lag et tverrsnitt av et skip og vis hvordan G'en flytter seg.
Oppgave 3. Sprekk i ballast tank
M/S Sidus går i den Engelske kanalen og det er oppdaget en sprekk i fra ballasttank WB WT 5P inn på lasterom 9. M/S Sidus har losset deler av lasten i Le Haver og er på vei til Rotterdam. Ballasttanken er beregnet til å være full, når styrmannen ser i toppen av lasteromsluken ser han at huller er sirka i midten av ballast tankens høyde, så han kalkulerer med at sirkla halvparten av vannet vil renne over i lastrom 9 i løp av de neste timene. Det har begynt å danne gass (Hydrogen) i lasterommet, siste last i rommet var Siliconmanganese. Vannet kan heller ikke pumpes ut, da det kan føre til forurensning. Skipet lå uten list før vannet begynte å renne ut fra ballasttanken og inn på lasterommet.
Skipsdata: ∆ 36 215 tonn og en KG2 12.71 meter.
a) Kapteinen lurer på om du kan beregne listen/krengningen skipet vil ha dersom halvparten av vannet renner over?
Svar: 7,75°Vi går ut ifra at skipet lå uten trim og at den er uforandret etter lekkasjen.
b) Hva er nå skipets dypgående på grunn av krengningen?
Svar: 10,627 mc) Hvor mye må eventuelt fyllest i WB WT 4P for å kompensere for krengningen?
Svar: 250,6 tonn
Oppgave 4. Dekkslast med M/S Sidus
M/S Sidus laster dekkslast på babord side, vekt på 35 tonn, vcg 32 meter, tcg 14 meter, ∆ før lasting er 35000 tonn og KG er beregnet til 12 meter.
a) Beregn hvor mange grader skipet krenger.
Svar: 0.53° til babord
Dersom en bunkrer 200 tonn HFO på FO 21 SB (styrbord) bunkerstanken, gå ut ifra at tanken var tom før bunkring.
b) Hva blir krengningen etter bunkring?
Svar: 0.5° til Styrbordc) Hvordan ville du kompensere for å få skipet uten (list) krengning?
Svar: Ved å fylle ballast i WB 3 WP 33 tonn
2.2.5. Finne tilnærmet krengevinkel av: tan Ø = TCG1 / GM & GZ-kurven der GZ = TCG1 & økt dypgående grunnet krengning.
Oppgave 1. Økt dypgående grunnet krengning
Et skip har en bredde på 18 meter, og dypgående uten Krengning på 12.85 meter.
a) Hvor dypt stikker skipet når det krenger 5°?
Svar: d1 = 13,586 m
Formel
$d1 = \frac{B}{2\ }$ x sin Ø + d x cos Ø
Oppgave 2. Økt dypgående grunnet krengning på M/T Millennium
M/T Millennium har et dypgående uten krengning på 22.33 meter.
a) Hvor dypt stikker skipet når det krenger 5°?
Svar: d1 = 24,77 m
Oppgave 3. Økt dypgående grunnet krengning på M/S Sidus
M/S Sidus har et dypgående uten krengning på 12.05 meter.
a) Hvor dypt stikker skipet når det krenger 5°?
Svar: 13,35 m
Oppgave 4. Krengning, økt dypgående og kontravekt på M/S Mercandian Importer.
MI har et dRef på 5.07 meter og TCG 0.03 meter port og skal laste en konteiner på 20 tonn med en tcg 4 meter port. Skipets KG er beregnet til 4.8 meter og lastens Kg er 8 meter. Gå ut ifra at MI har en bredde på 13.02 meter.
a) Hvor mye krenger MI og hva blir det nye dypgående med krengningen?
Svar: Krengning 5,2° & d1 5,663 mb) Hvor mye kontravekt må vi fylle i ballasttank No. 3 styrbord for å ligge uten list etter lasting?
Svar: 42,5 tonn
Oppgave 5. Krengning, økt dypgående og kontravekt på M/S Mercandian Importer.
MI har et T Ref på 4.05 meter og TCG 0.10 meter port og skal ta om bord et tungløft på 80 tonn med tcg på 3.5 meter port. Skipets KG er 4 meter og lastens kg er 8 meter. Skipet har en samlet FS på 156 tm. Gå ut ifra at bredden på MI er 13.02 meter.
a) Hvor mye krenger MI og hva blir det nye dypgående med krengningen?
Svar: 9,8° & d1 5.20 mb) Hvor mye kontravekt skal en fylle i ballasttank 3 og 5 styrbord for å ligge uten list?
(Svar: 125 tonn/ikke plass)
Oppgave 6. Krengning og kontravekt M/S Mercandian Importer
MI har et T Ref på 5.20 meter og TCG 0.03 meter port og skal laste 2 kontainere på 12 tonn hver med en tcg 2.0 meter styrbord. Skipets KG er 4.8 meter og lastens Kg er 7.8 meter.
a) Hvor mye kontravekt må du bruke for å holde skipet uten krengning. Bruk ballast WT 3 S TCG 2,25 meter?
Svar: 27,6 tonn
Oppgave 7. Krengning med M/S Linda
Det er tatt om bord en last med en 20 tonns kontainere på Linda. Kontainerne blir plassert på dekk med tyngdpunkt 14 m over kjøl. Etter lasting er skipet tilnærmet even keel og har et deplasementet 15000 tonn og en VCG på 8,00 m. For å bedre stabiliteten flyttes 10 av kontainerne ned i lasterommene, slik at vcg for kontainerne som flyttes er 10 m lavere.
a) Beregn KG og GM etter at kontainerne er flyttet.
Svar: KG1 7.867 m, GM 0.683 m
Etter at kontainerne er flyttet krenger skipet. Du kontrollerer plasseringen og finner ut at 5 kontainerne er plassert 9 m fra senterlinjen til fartøyet (alle var i senterlinjen før de ble flyttet).
b) Hvor stor er krengevinkelen?
Svar: 5,02°c) Hva blir dypgående etter krengning?
Svar: 7.427 m
2.2.6. Beskrive og beregne hvordan skipet rettes opp ved: Skifte vekter om bord, ta inn ballast & ta inn/ut vekt i gitt posisjon.
Dersom en kan transfere ballast fra den ene siden til den andre vil en redusere tiden og vekten en eventuelt bruker på å laste lasten:
Eks:
Dersom en skal rette opp et skip som ligger med et kr-mom på 440 tm, kan en ta kr-mom delt på avstanden fra punktet skipet krenger rund (normalt CL). Dersom en ser for seg at dette skipet er M/S Mercandian Importer vil en normalt velge den ballast tanken med størst tcg. Tank 3 og 5 P/S har en tcg på 4,4 meter. Da tar vi kr -mom (tm)/ avstand (m) = vekt som må fyllest (t). Dersom en har ballast inne er det lettest å transfere/flytte ballasten dersom en kan flytte fra 3 p til 3 s vil armen bli dobbelt så lang, og en flytter bare halvparten av mengden (momentet blir det samme).
Eks: Fylling av ballast =$\ \frac{440\ tm}{4,4\ m}$ = 100 tonn
Eks: Flytting av ballast =$\frac{440\ tm}{8,8\ m}$ = 50 tonn
Oppgave 1. Rette opp krengning/list med fylling/flytting av ballast
M/S Sidus ligger med 3° list til babord side og deplasementet er 43357 tonn. Skipets GM er 1,20 meter.
a) Hvor mye ballast må en fylle i WB 4 S for å kompensere for listen?
Svar: 192.56 tonnb) Dersom en heller hadde valgt å transfere ballast mellom WB 4P til WB 4S, hvor mye måtte en transfere?
Svar: 96.3 tonn
Når en skal endre trimmen på et skip brukes normalt trimtankene, dette er normalt de to ballasttankene som er lengst vekke fra hverandre i langskipsretning som blir benyttet for å trimme skipet. På tankskip er det ofte normalt å bruke lastetankene og transfere last mellom de to tankene, på M/T Millennium ser jeg for meg at C.O.T 1 C og C.O.T 5 C blir brukt.
Oppgave 2. Flytte ballast for å oppnå ønsket trim på M/S Sidus
M/S Sidus har en trim på 62 cm akterlig når hun ankommer kaien i Rotterdam, skipets deplasement før lastingen av siste partiet med konteinere kan begynne er 39489 tonn. Du har fått i ansvar å legge skipet uten trim. Akterpeaken er fylt opp med sjøvann, mens forepeaken tanken er tom.
a) Hvor mye må transferes for å ligge uten trim (even keel)?
Svar: 193,9 tonn
Når en skal rette opp skipet for trim ved å fylle ballast eller lense ballast, må en ha i bakhode at CF (LCF) flytter seg.
Dersom en fylle mye ballast vil CF (LCF) flytte seg, dette er p.g.a at vannlinjearealet endrer seg når deplasementet øker på et skip. En vil ha samme problemstilling dersom en lenser ballast for å oppå ønsket trim, men da vil normalt vannlinjearealet avta.
Oppgave 3. Rette opp skipet som ligger med trim, ved å fylle ballast
M/S Sidus ligger med en trim på 12 cm akterlig, du skal legge skipet uten trim ved å fylle sjøvann i forepeaken. Skipets deplasement før fylling var 40 022 tonn.
a) Hvor mye må man fylle for å ligge even keel?
78.5 tonn
Først må vi finne trimmomentet og dele det på avstanden fra CF (LCF) til forepeaken tanken.
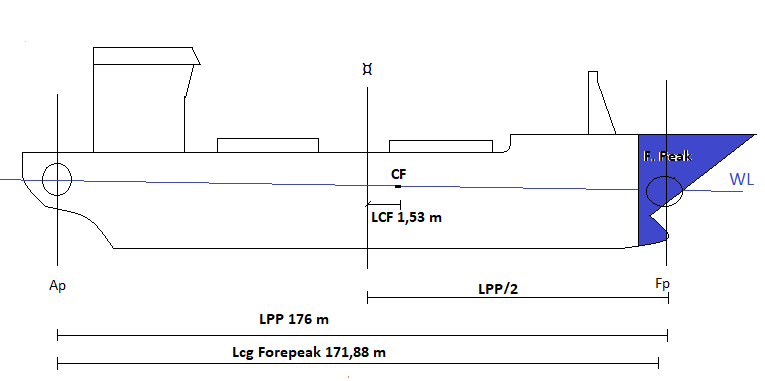
- Trimmoment = Trim x MTC = 12 cm x 538,40 tm/cm = 6460,8 tm
- Avstand CF til Forepeak = Lcg - L/2 - LCF = 171,88 m - 176/2 - 1,53 m = 82,35 m
Vekt å fylle i forepeak for å komme even keel = 6460,9 tm/82,35 m = 78,5 tonn
b) Dobbeltsjekk trimmen med å laste lasten du kom frem til og finn nøyaktig trim etter fylling av ballasten.
Svar: 0.08 cm
Oppgave 4. Legge M/S Sidus uten trim ved å fylle ballast
M/S Sidus ankommer New York lastet til et deplasement på 37 000 tonn, med en akterlig trim på 120 cm. Du skal legge skipet even keel ved å fylle ballast i forepeak tanken.
a) Hvor mye må du fylle for at skipet er even keel ved avgang?
Svar: 753 tonnb) Kontroller opp mot tradisjonell metode, der du laster lasten du har kommet frem til for å finne nøyaktig trim. Diskuter hvorfor skipet ikke ligger helt even keel.
Svar: 0,39cm
2.2.7. Angle of Loll
Hvis et skip har negativ GM, vil ikke skipet ha et opprettende moment på små vinkler, og den rettende armen, GZ, vil være negativ. Angle og loll er de gradene på GZ-kurven som er negativ, som vi ser på figuren under, er fra 0ᵒ til cirka 10ᵒ. Hvis en ytre påvirkning gjør at skipet krenger til en vinkel hvor skipet ikke har et rettende moment, vil ikke skipet rette seg opp av seg selv før krengningen blir like stor som når GZ-armen er positiv igjen. På figuren vil det være ved 10ᵒ. Vi ser at skip som har negativ begynnelsesstabilitet og negativ GZ-arm likevel kan ha positiv stabilitet ved større krengninger.
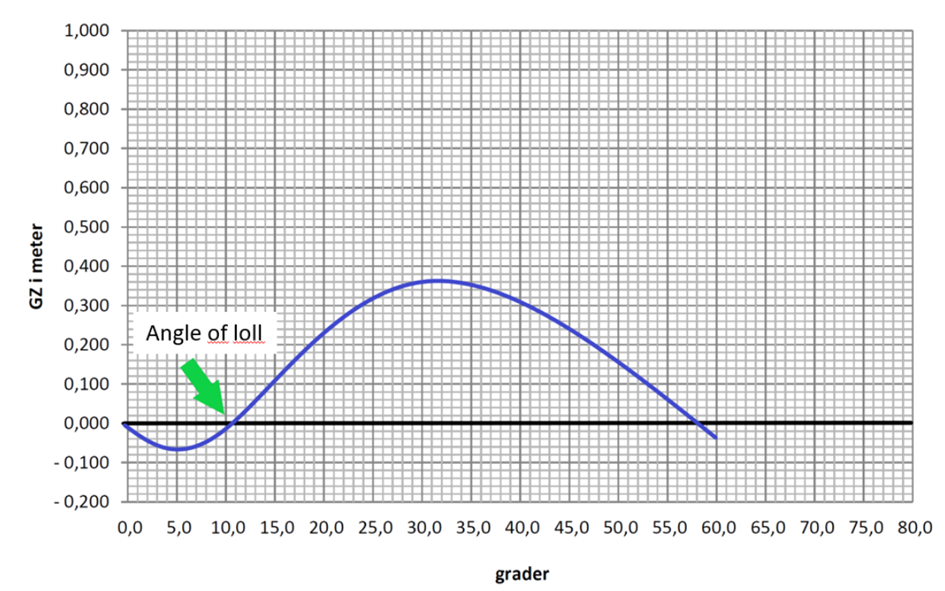
Grunnen til at stabiliteten blir positiv ved krengning i dette tilfellet er at når skipet krenger, øker bredden til skipet. Når bredden øker, vil skipets BM øke. Når BM øker blir avstanden mellom skipets G og M større og skipet slutter å krenge når det har oppnådd en labil GM på 0.
Test av GZ-kurve med M/S Sidus ved positiv og negativ stabilitet for å finne GM0.
- ∆ 40 931 tonn, KMT = 13,24 m, KG2 = 12,74 m
- G2M = KM - KG2 = 13,24 m - 12,74 m = 0,50 m
- Bruker 40 900 tonn for å finne KN.
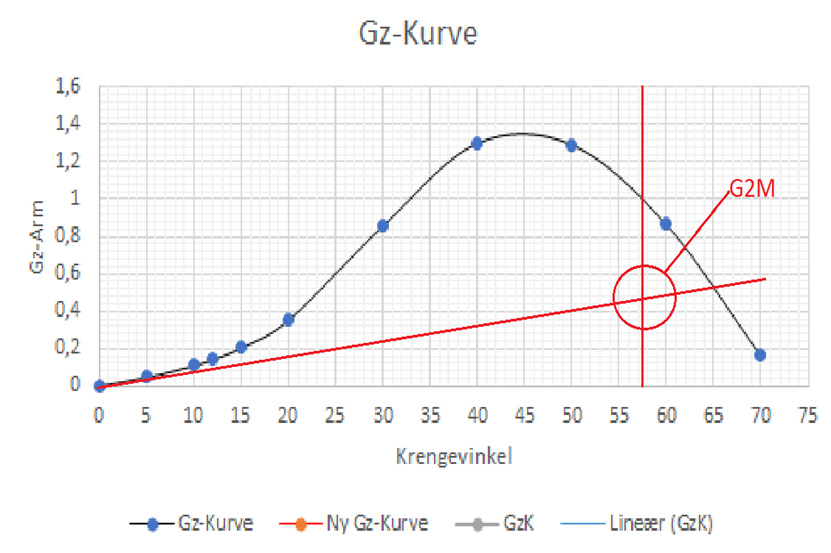
- ∆ 40 931 tonn, KMT = 13,24 m, KG2 = 12,74 m
- G2M = KM - KG2 = 13,24 m - 13,34 m = -0,10 m
- Bruker 40 900 tonn for å finne KN
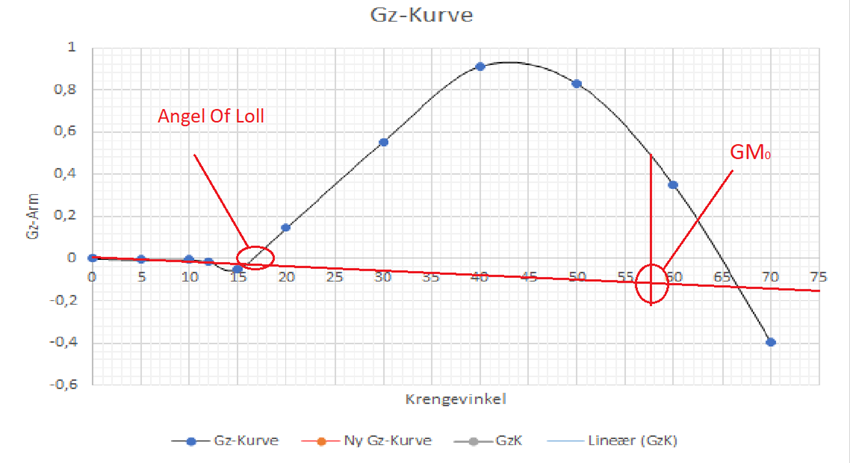
Oppgave 1
a) Hva er angel of loll?
b) Hvordan vil et skip oppføre seg dersom det har negativ begynnelsesstabilitet?
2.3 Tungløft

Bilde av Heerema Sleipnir, som løfter på plass en av delen til Johan Sverdrup. Kapasitet 10 000 tonn på hver krane.
2.3.1 Beregne virkningen på stabilitet og krengning ved lasting, lossing eller skiftning av tunge vekter.
Oppgave 1. Lasting av tungløft
M/S Linda skal ta om bord en lekter på 50 tonn, Linda har et dypgående før løftet på 7,5 meter even keel. Lekteren skal heises om bord med egen krane. Lekteren ligger på kaien med en avstand på 6 meter fra skutesiden til tyngdepunkter på lekteren. Høyden på kranen er beregnet til 22 meter under løftet, skipets GM før løftet skal tas er beregnet til 1,1 meter.
a) Hva er Lindas GM når løfte er klar av kaien?
Svar: 1,058 mb) Hvor mye vil Linda krenge i det løftet er klart av kaien?
Svar: 2,5°
Oppgave 2. Lossing av tungløft
M/S Mercandian Importer er lastet til WNA, med variert stykkgodslast. Det skal stoppes for å losse en gravemaskin type Volvo EC 380E på 40 tonn og en hjullaster type Volvo L110 H på 20 tonn, dette skal losses på et anleggsområde. Grunnet dårlig kai må lasten svinges ut hele 7 meter fra skutesiden. Lasten har stått på lukene som har blitt forsterket i anledning. Vcg på disse anleggsmaskinene var 10,30 meter, GM før lossingen var på 1,2 meter. (Gå inn på side 14 i M/S Mercandian Importer plansje, her finner du VCG'en på kranen).
a) Hva blir skipets GM når siste lasten er losset (gravemaskinen losses sist)?
Svar: 1,274 mb) Hvor mye blir skipets krengning når kranen er svinget helt ut med siste lasten?
Svar: 6,85°
Oppgave 3. Lossing av tungløft
M/S Linda skal losse et tungløft på 100 tonn, Linda ankommer even keel og er lastet til et deplasement på 21 210 tonn. Skipet har en beregnet KG2 på 8,04 meter. Man regner med at lasten vil bli svinget 20 meter ut fra senterlinjen, toppblokken er 22 meter over kjølen. KG på lasten som skal losses er 15 meter.
a) Hva er skipets GM når lasten lettes av dekk?
Svar: 0,557 mb) Hva er maks krengning under lossingen?
Svar: 9,28°
Oppgave 4. Lossing av tungløft, slakke tanker og stabilitet
Et skip har følgende hoveddimensjoner:

Ved en gitt lastekondisjon har skipet følgende data:
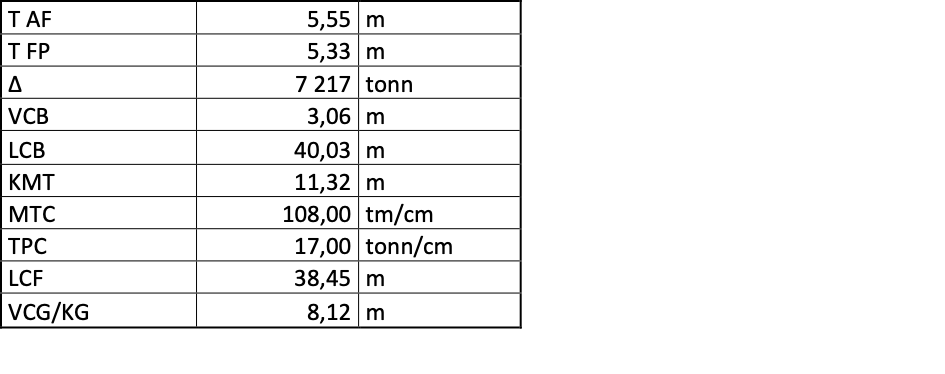
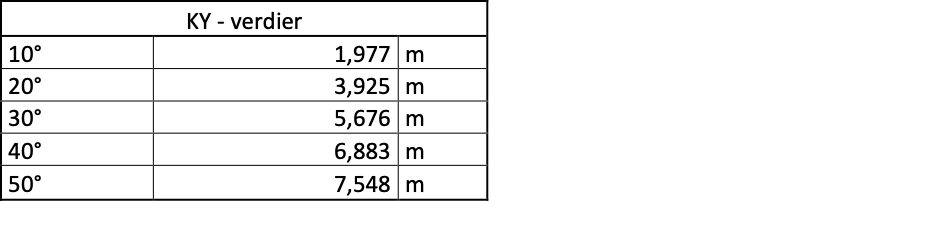
Skipet har "Slakke" tanker med følgende overflater:
- IT (ferskvannstanker: P = 1,0 tonn/m³): 741 m4
- IT (ballast tanker: P = 1,025 tonn/m³): 351 m4
- IT (bunkerstanker: P = 0,86 tonn/m³): 1680 m4
Under overfarten har skipet en ankomst kondisjon som beskrevet.
a) Hva er skipets G2M?
Svar: 2,872 mb) Er denne kondisjonen i overensstemmelse med de generelle kravene til intakt stabilitet for skip på 50 tonn og derover?
Svar: ja
En last som veier 100 tonn losses ved hjelp av skipets egen bom. Bomnokken er 20 m over kjølen, og lasten plasseres på kaien 15 m fra skipets senterlinje. Lastens KG før lossing er oppgitt til 12,5 meter.
c) Hvor mye krenger skipet under denne losse operasjonen?
Svar: 4,34°
Oppgave 5. M/S Mercandian Importer Lasting av tungløft - med kontravekt inne før løfting
MI ligger til kai og har avlest dypgående på følgende dF 4,02 meter dA 4,43 meter. Løftet skal tas om bord på styrbord side. Kapteinen ønsker å redusere krengningen og bedre stabiliteten før løfte skal utføres. Så han vil du skal beregne hva krengningen blir og økning av GM etter du har fylt opp ballasttank No. 3 P. KG2 er beregnet til 4,81 meter før kontravekten tas om bord.
a) Hva blir ny G2M og krengning med kontravekten inne?
Svar: GM=0,548 m, Krengning 6,17° babord
Løftet er på 42 tonn og kranens TCG under løftet er 11 meter, VCG er 16 meter.
b) Hva blir krengningen når løftet er klart av kaien?
Svar: 14° styrbord, beregnetc) Drøft fordeler og ulemper med å bruke kontravekt i dette tilfellet.
2.3.2 Beskrive og beregne bruk av ballast og skiftning av last som «motvekter» for å redusere krengning
Oppgave 1. Tungløft med Mercandian Importer
M/S Mercandian Importer har avlest dypgående Tf 4.77 m Ta 5.67 m og KG utregnet til 4.65 m. Sjøvannets tetthet 1,025 t/m³. Man skal laste et tungløft på 40 tonn som plasseres på styrbord side av luke 1. Man regner med at lasten vil ha en lcg på 50 m og avstand fra senterlinje på 5 m. Skipets eget gir skal brukes og toppblokken er festet 20 m over kjølen, samt bommens utsving 12 m fra senterlinje.
a) Beregne skipets krengning i det løftet henger i kroken.
Svar: Kr.v 11,80°/GZ-kurve kr.v 11,1°.b) Hva blir skipets dypgående ved denne krengningen?
Svar: 6,44 mc) Hvor mange tonn ballast må man fylle på tank #2 og #3 for å få skipet rett i det løftet er plassert på dekk. Ballasten fordeles likt på begge tankene og tyngdepunkt regnes 4,25 m fra senterlinje?
Svar: 47 tonnd) Beregne skipets dypgående etter at man har lastet tungløft og ballast.
Svar: df 5.06 m d¤ 5,333 m da 5,61 m
Oppgave 2. Tungløft med Mercandian Importer
M/S Mercandian Importer dypgående er Tf 2.85 m Ta 3.40 m og KG beregnet til 4.75 m. Man skal ta om bord et tungløft på 25 tonn og det er ingen slakke tanker. Feste for toppblokken er 20 m over kjølen og bommen er svingt 3.5 meter fra skutesiden.
a) Hvor stor krengning fikk skipet idet løftet henger i bommen?
Svar: 10,1°b) Hva ville krengningen blitt dersom man fyller opp tank # 3 på motsatt side? Tanken tyngdepunkt regnes 4,40 m fra diamentralplanet.
Svar: 2,86°
Oppgave 3. Tungløft og maks. Krengning 5°
M/S Mercandian Importer skal laste et tungløft på 50 tonn med eget gir. Dypgående avlest før lasting var Tf 4.80 m og Ta 5.20 m og KG beregnet til 4.50 m. F.O. tank # 4 og F.W. tank # 6 var slakke. Bomløftet var festet 13 m over dekket og lastebommen svinget 4 m utenfor skutesiden idet tungløftet ble tatt om bord.
a) Beregne skipets krengning idet løftet henger i kroken.
Svar: 11,6°b) Hvor mange tonn ballast må man ta inn på motsatt side når tyngdepunktet i tanken regnes 4.25 m fra senterlinje og man ønsker maksimalt slagside 5° under lasting av tungløft?
Svar: 67,2 tonn
Oppgave 4. Lasting tungløft og maksimalt utslag hvis løfte ryker
M/S Mercandian Importer ligger med styrbord side til kai med dypgående avlest F 3.80 m, A 4.50 m og KG beregnet til 4.5 m. Man skal laste et tungløft på 35 tonn og bruker eget gir (gear). Festet for toppblokken er 20 m over kjølen og bommen legges ut slik at avstanden fra skipet senterlinje og til mantelwiren er 10 m.
a) Hvor stor slagside må man regne med skipet vil få i det løftet henger i kroken?
Svar: 11.2°b) Man ønsker imidlertid å fylle ballast på bunntank nr. 2 babord for å unngå altfor stor krengning. Tankens tyngdepunkt (tcg) ligger 4 m fra senterlinjen, hva blir krengningen etter ballasten er tatt om bord?
Svar: 6,34°c) Bestem maksimum utslag dersom løfte ryker ved bommen maksimum utsvingning?
Svar: ca 12°ved kontravekt inned) Gjør rede for forholdsregler man bør passe på ved lasting av tungløft?
Oppgave 5. Tungløft og stabilitet ved lossing
M/S Sidus har avlest dypgående på 9.00 m "Even Keel", Skipets VCG er 12.20 meter før lossing. 175 tonn skal losses med eget gir med en tcg 11 meter (styrbord side) og vcg på 24 meter. FP, AP og WT WB 3P/S er alle 40% fulle.
a) Hva er G2M før lossing?
Svar: 0,836 mb) Hva er G2M i det løftet lettes fra skipet?
Svar: 0.776 m
Toppen av kranen er 37 meter og levering er 11 meter fra skutesiden på babord side.
c) Hva blir størst krengevinkel uten bruk av ballast?
Svar: 10,1° ved GZ-kurve & uten GZ-kurve 12,6°d) Hva blir dypgående ved denne krengningen?
Svar: 11,6 meter
Oppgave 6. Tungløft og trim med lasting
M/S Sidus skal laste 150 tonn med egen krane på styrbord side. Kondisjonen før lasting er "Even Keel" T ref 10.50 meter og KG 11.85 m. Lasten veier 150 tonn, forventes å bli tatt 10 meter fra skutesiden og topp av kranen er 36 m over kjølen. Lasten skal plasseres på luke 5 med en tcg på 10 meter og en vcg på 25 meter. HFO 21 P/S og FW 40 P/S er 40% fulle
a) Hva er krengevinkelen i det løfte tas og etter at det er plassert på luken?
Svar: S 3,8°/ B 1,45°b) Hvor mange tonn må det kompenseres med i WB WT 3P og hvor mye må transferes til WB WT 3S etter løfte er plasser på babord siden?
Svar: kompensere 268 tonn/Vekt å flytte 186,7 tonnc) Hva blir trimmen etter vekten er plassert på luken og ballasten er om bord?
Svar: 4,5 cm forlig trim
Oppgave 7. Tungløft, stabilitet og trim med lasting
M/S Sidus skal laste 180 tonn med egen krane. Lasten tas 12 meter fra skutesiden, toppen av kranen er 38 meter. Lasten skal plasseres på luke 6 med en vcg på 25 meter og en tcg på 10 meter.
Skipets avlest dypgående er TF 10.50 meter og TA 10.05 meter i vann med densitet 1.025 t/m³. KG er 12 meter. Det er følgende slakke tanker FP, AP og WT WB 3P/S er alle 40% fulle.
a) Hva blir krengevinkel i det løftes tas og i det lasten er plassert?
Svar: 7,3°b) Hvor mye ballast må en flytte mellom WT WB 3S til 3P for å holde skipet uten krengning når løfte heves fra kai?
Svar: 173,6 tonn
Oppgave 8. Tungløft med Mercandian Importer
M/S Mercandian Importer er lastet til 5.43 meter even keel (skala) og skal ta om bord to store betongelementer på 29 tonn hver som skal plasseres på luke 2. Du skal bruke ballast tank DB3P/DB3S som har en TCG på 4.4 meter (ha tanken full når du turner rundt skipet).
Etter lastet første betong elementet på babord side, skal skipet tørnes rundt og laste styrbord side. Det er maks dypgående på 5.7 meter ved kai.
TCG før lasting er 0.03 meter babord, VCG på betongelementene er 8.5 meter/ LCG 28 meter/ TCG 4 meter og KG er beregnet til 4,58 meter før lasting og skipet har FSM på 258 tm.
Vi går ut ifra at skipets luker tåler belastningen av betongelementene.
a) Hva blir dypgående når vi tørner skipet rundt forut, akterut og midtskip på styrbord og babord side midtskips?
Svar: df 5.54 m, da5.49 m, d¤S 5,405 m & d¤b 5,623 m
Oppgave 9. M/S Sidus de tre aksene
M/S Sidus har dypgående dRef 9.41 meter og trim på 1 meter akterlig. M/S Sidus skal laste kontainere med en snitt vekt på 12 tonn/kontainer på babord side Tier 82 og 84. Styrbord side er alt lastet ombord. Dypgangen ved kai er satt til maks 10.70 meter. Bruk ballast i WB WT 3S og WB WT 4S for å kompensere for krengning.
TCG/YCG før lasting er 0.03 meter.
M/S Sidus har en samlet FSM på 3628 tm.
TCG/YCG kontainer babord side er 6.2 meter.
KG før lasting er beregnet til 9.29 meter.
a) Se om skipet følger stabilitetskrav i henholdt til GM, GZ V/30 og GZ-maks.
Svar: G2M-3.138 m, GZ-30°- 2.137 m & GZ-max ca - 50°b) Hva blir skipets kondisjon i henholdt til dypgang dersom en kompenserer med ballast i WB WT 3 & 4 S?
Svar: dref 10,14 m & trim 106,5 cmc) Hvordan kan vi ta et enkelt grep og komme oss under maks tillatt dyppende ved kai?
Svar: Hint bruk flotasjonsmetoden i formelsamlingen/dref - 10,29 md) Forklar hvordan du ville gjord dette teoretisk. Og hvorfor det er så viktig og ikke krengning under lasting og lossing av kontainere?
Oppgave 10. M/S Sidus dekkslast
- T referanse (TRef) er 5 m og KG er beregnet til 16 meter før lasting skipet ligger uten trim og list.
En skal laste følgende:
| Hva | vekt | Tcg | Vcg | Lcg |
|---|---|---|---|---|
| FEU -cont. | 30 | 4 m (babord) | 22.98 m | 90.5 m |
| 4 Bulldosere | 75 | 8 m (babord) | 22.98 m | 80.7 m |
| Boretårn | 120 | 3 m (styrbord) | 22.98 m | 120.0 m |
a) Hva blir dypgående etter lasting?
Svar: TF 5.089 m T¤ babord 5.348 m, T¤ Styrbord4.782 m, TA 5.041 mb) Hvor mye ballast må du fylle i WB WT 3 S og AP for å ligge uten list og trim etter lasting?
Svar: WB WT 3 S 25,5 tonn og AP 21,2 tonnc) Hva blir stabiliteten etter du har fylt ballast, full stabilitets kontroll?
Svar: G2M = 0,981 m, GZ 30°= 0,194 m < 0,20 m & GZ-maks før 30° (Stabilitet ikke ok)
Oppgave 11. M/S Sidus krengning
M/S Sidus skal ta et siste løft før det er ferdig lastet. Løftet veier 80 tonn og skal tas med to kraner. Løftet står 8 meter fra skutesiden.
Dypgående før løftet tas er 11,516 m og skipet er «even keel». KG ukorrigert er 12,50 meter og samlet FS-mom er 2900 tm. Kranens toppunkt er 12 meter over dekk.
a) Beregn krengevinkel i det løftet tas.
Svar: 2,9°b) Løftet skal plasseres på luke 4 med tcg 7 meter og vcg 24,3 meter. Hva blir krengevinkel når dekkslasten er plassert på dekk?
Svar: 0,86°c) Hva blir største dypgående under løftet?
Svar: 12.321 md) Hvor mange tonn sjøvann må fylles på DB3 PS for å unngå krengning (skipet skal ligge uten list)?
72.8 tonn
2.3.3 Kjennskap til opplysninger skip utstyres med for å ha kontroll med tungløftsituasjoner
Opplysninger skipet skal ha før tungløftoperasjonen skal gjennomføres:
- Tungløftets vekt, dimensjon.
- Avstand vekten plasseres fra kai.
- Dersom feste/løkker på tungløftet MSL/SWL på festene.
- Dypgang ved kai.
- Værmelding.
- Lastens plassering om bord.
2.3.4 Drøfte faremomenter og forholdsregler, og beskrive faren for store rulleutslag dersom løftet «ryker».
Når løftet ryker uten kontravekt:
(formelhefte, marfag)
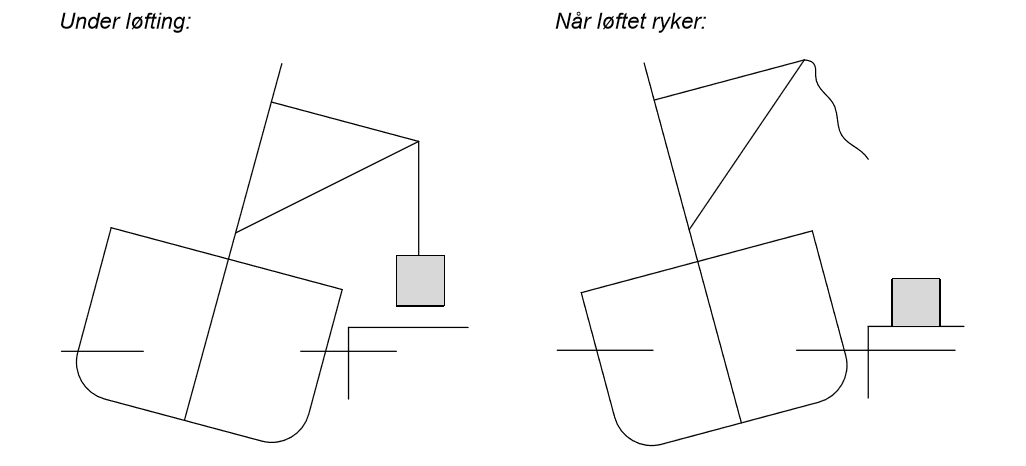
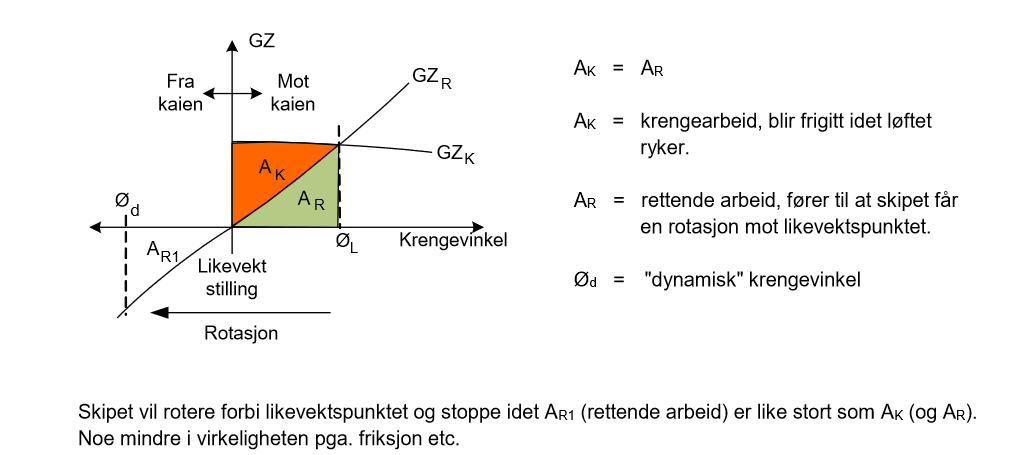
Når løftet ryker med kontravekt:
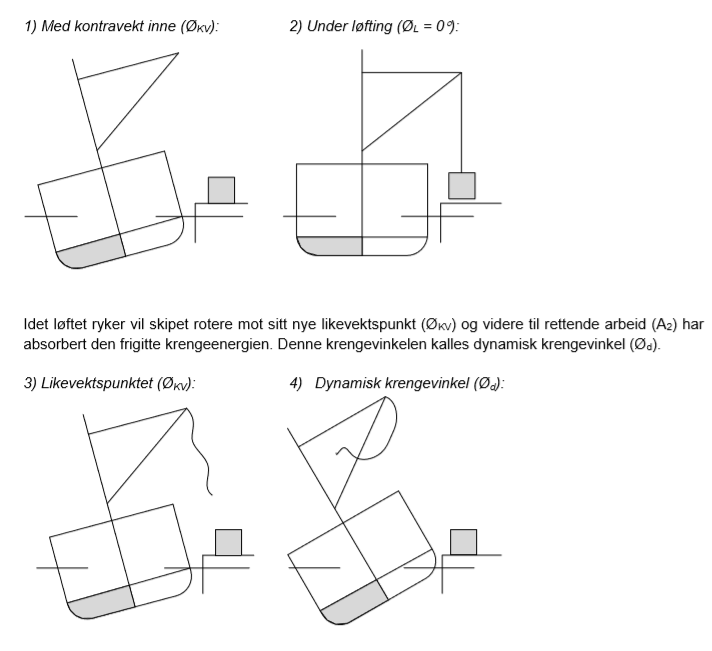
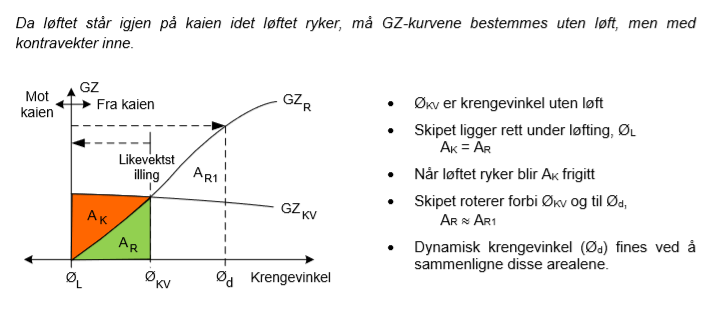
Oppgave 1. M/S Mercandian Importer
MI skal laste 3 moduler i underrom 2. Hver modul veier 50 tonn. Bruk rommets lcg og vcg ved lasting av modulene.
Avlest dypgående er Tf 3,70 m Ta 4,70 m og KG er beregnet til 4,50 m.
a) Hva blir dypgående og KG etter last?
Svar: KG 4,411 m & df 3,716 m, d¤ 4,389 m, da 5,062 mb) Du velger å gjøre en beregning over krengningen i det siste modul kommer om bord. Hva blir krengningen?
Svar: 14,42°
Du vurderer at kranen vil strekke 11 meter ut fra senterlinjen og topp av kran 14 meter over kjølen.
c) Beregn GZ-kurven under løftet.
d) Hva ville hendt dersom løfte røk?
Oppgave 2. Tungløft med Mercandian Importer
M/S Mercandian Importer skal ta et tungløft på 55 tonn. Før løftet tas om bord har skipet et ∆ 3504 tonn og KG 4,3 m. Bomnokken er 21 meter over kjølen, og løftet tas på styrbord side, 8 meter fra diametrialplanet (CL).
a) Hvor mange grader vil skipet krenge når løftet er klart av kaien?
Svar: 8.5° ved beregning 8° ved kurveb) Eks: Hvor mye ballast måtte vi hatt om bord for å være uten list når løfte ble tatt? Bruk ballast tank 3 P og 5 P.
Svar: 100 tonn fordelt likt på 3 P & 5 Pc) Hva vil hende dersom løfte ryker med ballast inne? Lag tegning og forklar.
Oppgave 3. Tungløft med Mercandian Importer
M/S Mercandian Importer skal ta om bord en 40 fots kontainer på 30 tonn. Skipet har et deplasement på 3600 tonn og en KG beregnet til 4,90 m. Når løftet tas er bom-blokkens høyde over kjølen 21,00 m, og bommen er utsvinget 10 m fra senterlinjen. Skipet ligger med styrbord side til kai, og det er ingen slakke tanker om bord.
a) Finn skipets krengevinkel i det løftes lettes fra kai.
Svar: 12.7° til styrbord ved beregningb) Sammenlign krengningen med å bruke formler kontra med å finne krengevinkelen ved bruk av kurve.
Svar: 11° til styrbord ved GZ-kurvec) Hva er skipets stabilitet etter at løftet er satt på plass (vcg til konteineren er 9,60 m)?
Dersom en ønsker krengning på under 10° ved løftet, hvor mye ballast må en fylle?
Hint:
Formel ønsket GM: $øGM = \frac{\text{v x tcg}}{\mathrm{\Delta}\text{ x}\tan o}$
Ønsket G og KG under løfting: KM - øGM = øKG
Må senke skipets G: KG under løfting - øKG under løfting = GG1
$V = \frac{\mathrm{\Delta}\text{ x GG}1}{a}$
d) Finn ny G og krengevinkel.
Oppgave 4. Tungløft med loss of load
Et skip med et deplasement 20 000 tonn og KG på 8,15 meter, skal ta om bord et tungløft på 300 tonn med egen kran. Kranens bommen ligger 22,0 m innover kaien fra skipets senterlinje og bomnokken er 20 m over kjølen i det løftet tas. Skipets KM er 9.40 meter etter løftet er tatt om bord.
a) Hvor stor GM har skipet under løfteoperasjonen?
Svar: GM 1,165 mb) Beregn skipets krengevinkel i det løftet tas med bruk av formel?
Svar: 15,5°
For å få bedre nøyaktighet på størrelsen av krengevinkel må vi tegne opprettendearm-kurve (GZ) og krengendearm-kurve i samme system og avles likevekts punkt.
Følgende KY-verdier er gitt for kondisjonen:
- KY ved 7,5°: 1,18 m
- KY ved 15°: 2,60 m
- KY ved 30°: 4,80 m
- KY ved 45°: 6,76 m
- KY ved 60°: 7,34 m
- KY ved 75°: 7,62 m
Beregn og tegn rettendearm-kurve (GZ) og krengendearm-kurve og avlest krengevinkelen i det løftes tas.
c) Skipets bredde er 18 meter og dypgående før løfte tas er 8 meter even keel? Hva blir største dypgående under løfte?
Svar: 10,11 md) Dersom en hadde hatt kontravekt inne, ikke beregne ny KG (bruk tidligere GZ-kurve) hvor langt ville skipet ha krenget (Ød)?
2.3.5 Dypgangs økning midtskips ved krengning.
Har blitt gjennomført i punkt 2.2.5., vi tar en kort repetisjon.
Oppgave 1.
Dersom M/S Sidus er lastet til ∆ sommer even keel og tar et tungløft som gir de 3 grader krengning til styrbord.
a) Hva blir skipets dypgang på styrbord side?
Svar: 12,84 m
Oppgave 2.
Lasten har forskjøvet seg på M/S Mercandian Importer, ved avgang var MI lastet til WNA og hadde en GM på 0.45 meter, noe av lasten på Tween dekket har flyttet seg 4 meter til babord. En estimerer at vekten på lasten er 50 tonn. MI var uten trim og krengning ved avgang.
a) Hva blir skipets dypgående midtskips (styrbord og babord side)?
Svar: db 6,26 m d¤ 5,57 m ds 4,88 m

