Kapittel 2: En nærmere titt på stabilitet
Stabilitet
Stabilitet, ordet stammer fra det Greske språk, betyr at et skip har evne til å rette seg opp etter å ha blitt utsatt for krengning.
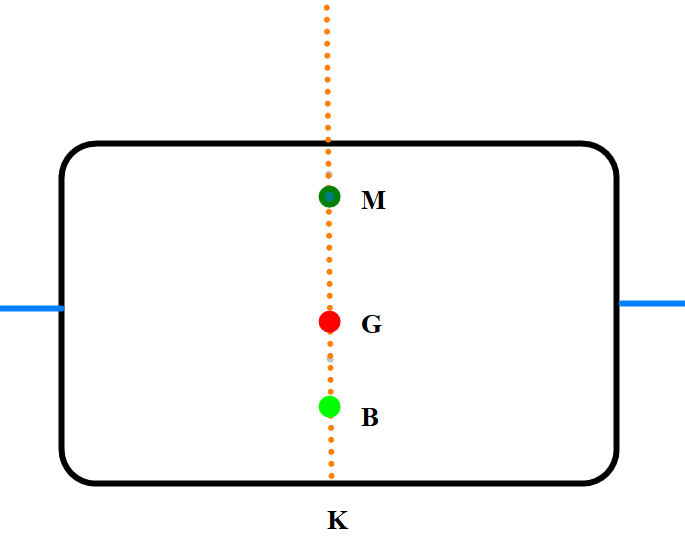
Figur 0201 Grunnleggende stabilitet (Initial stabilitet)
En nærmere titt på grunnleggende stabilitet (initial stabilitet)
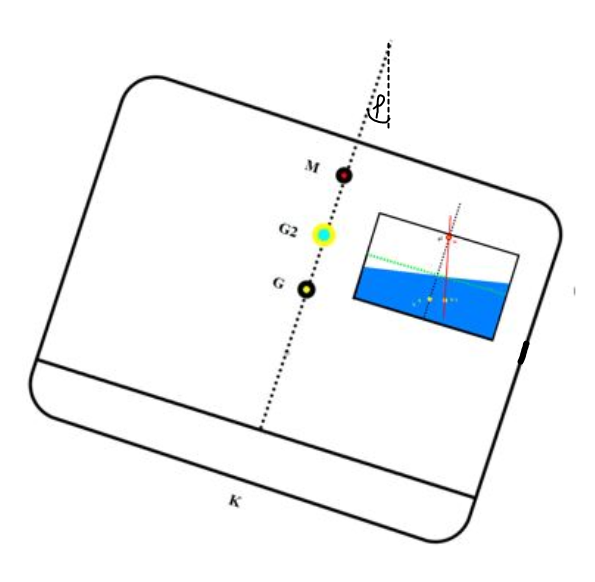
Med K (Kjølplate) som referansepunkt, B (oppdriftpunkt)), G (tyngdepunkt) og M (metasentre). Metasentret er et teoretisk tenkt punkt og er mye benyttet til stabilitets beregninger. Oppdriftkraften fra B går i gjennom M ved krengninger mindre enn 10 – 12°. Grunnleggende stabilitet (initial stabilitet) regnes opp til 10-12° krengning.
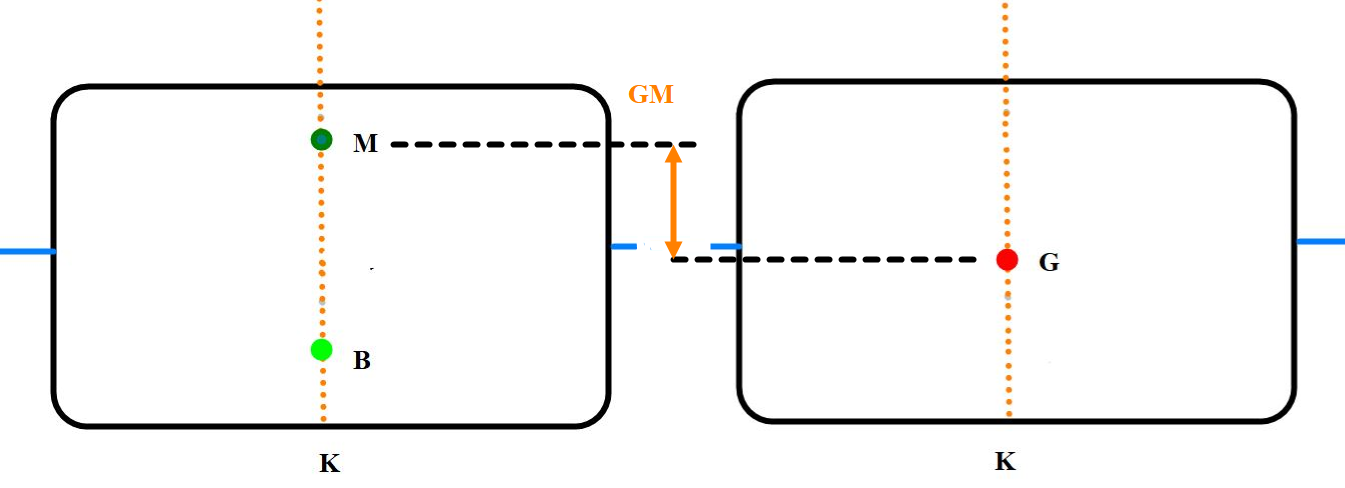
Figur 0202 Formstabilitet (venstre) og Vektstabilitet (høyre).
Den grunnleggende stabilitet deles inn i 2 forskjellige former, den ene er formstabilitet og den andre er vektstabilitet. Formstabilteten består av B (oppdriftpunkt) og M (metasentre). Et viktig bidrag til formstabiliteten er skipets bredde. Vektstabiliteten består kun av tyngdepunktet og den vertikale plassering er viktig for skipets stabilitet. K (kjølplate) er et referansepunkt for begge stabilitets formene. Formstabiliteten er bestemt av skipets konstruksjon, vektstabiliteten er delvis bestemt av byggherren sin plassering av komponenter om bord (Lett skip KG) men lasteoffiseren kan påvirke i stor grad med plassering av last, vekter om bord. Et skip kan ha god formstabilitet men dårlig vektstabilitet eller dårlig formstabilitet men god vektstabilitet. Den enkleste metoden for å ha kontroll med begge stabilitetsformene er med positiv GM (avstand fra skipets G til skipets M). Avstanden er forskjellige for forskjellige fartøytyper, for et vanlig handelsfartøy er kravet til GM = 0,15 meter eller større. Et fiskefartøy har krav til GM = 0,35 meter eller større. Sistnevnte har strengere krav fordi tyngdepunktet (G) er i forandring under fiske: bruk av kran, last og bruk på dekk, samt i lasterom, sjøvann på dekk, de fleste fiskefartøy vil bli påvirket av ising også. Det vil ikke la seg gjøre å gjøre å ha krav til KG (avstand fra K til G) fordi den vil være forskjellig fra skip til skip, den vil også variere etter hvor mye deplasementet er, Krav til KM (avstand fra K til M) alene vil heller ikke gi noen mening.
GZ betydning for stabilitet (rettende arm og Rettende moment)
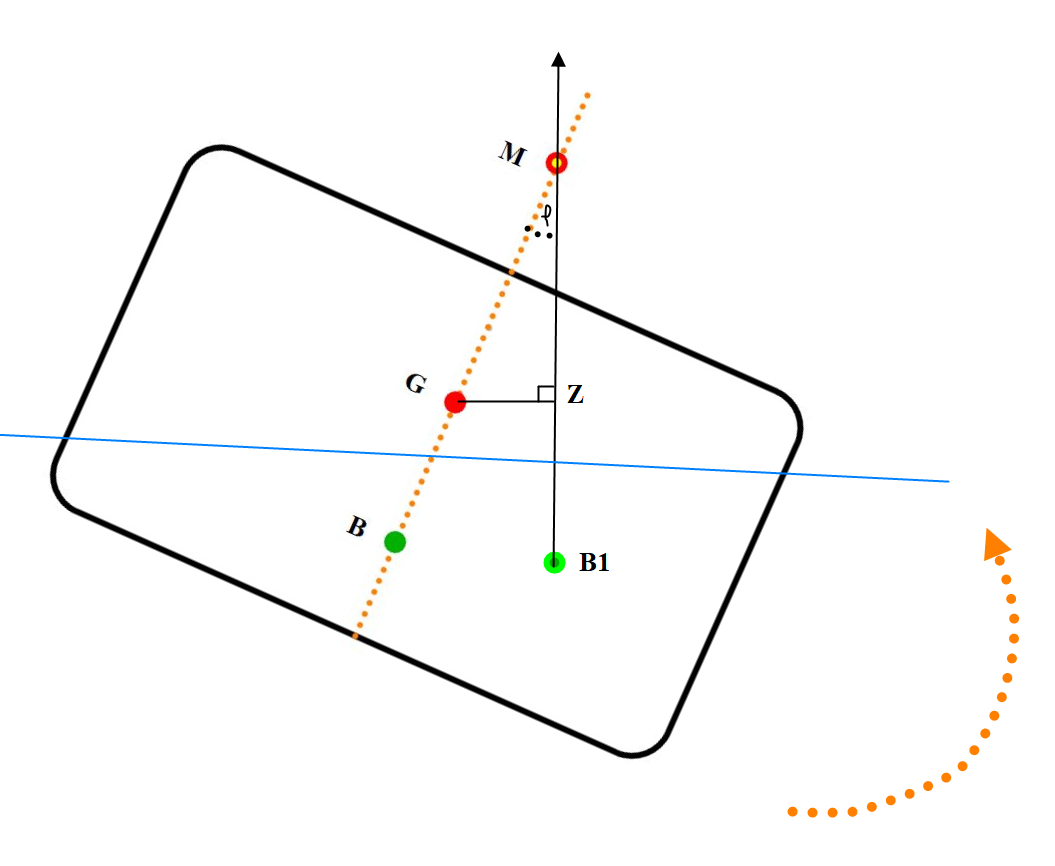
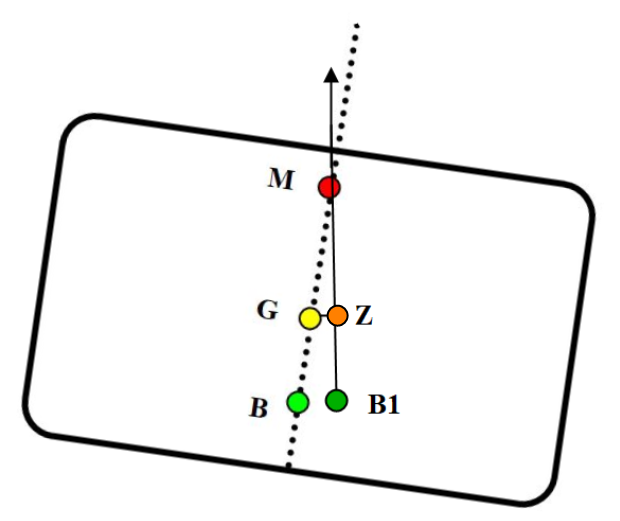
Figur 0203 Rettende arm og Rettende moment
Ved krengning så vil B (oppdriftpunkt) innta en ny posisjon ved B1, som er oppdrifpunktet sitt nye tyngdepunkt i volumdeplasementet fordi formen er endret. Ved krengning under 12° så vil oppdriftskraften gå i gjennom M (metasentre) fordi metasentre står i samme punkt.. Definisjon av metasentre er der hvor oppdriftkraften skjærer senterlinjen ved krengning under 12°. Det virker en tyngdekraft i gjennom G (tyngdepunkt) i motsatt retning enn oppdriftskraften (ikke tegnet inn). Så lenge last og andre gjenstander om bord er lastesikret så vil ikke G forandre posisjon. Avstand i mellom de loddrette kraftlinjene vil være den samme uansett hvor man måler på disse, men det er i fra G man tegner den. Punktet hvor den treffer oppdriftkraftlinjen kalles for Z. (kanskje Z har noe med zenit å gjøre?). Avstand GZ er den rettende arm og det rettende moment er GZ arm multiplisert med oppdriftkraften. Et moment er vekt x kraft, når kraften virker 90 ° på armen, men her er g (9,81 m/s3) forkortet bort slik at det rettende moment = Vekt x arm. Det rettende moment er: ∆ (Tonnes) × GZ arm (meter) = Tonnmeter. Det rettende momentet vil rette opp skipet (stiplet pil) slik som definisjon på stabilitet medgir. Ved krengninger under 12° så vil M (metasentre) stå i samme punkt. Det medfører at hvis man kjenner til GM og krengningsvinkel ($\varphi)\ $så kan GZ arm beregnes. Sin$\text{ φ}$ = GZ /GM → GZ = GM × SIN$\text{ φ}$. Større GM gir større GZ og større GZ gir bedre rettende moment.
Oppdriftkraft = Tyngdekraft (like stor men motsatt retning).
$\nabla$ × p × g = ∆ × g (forkortet bort g), $\nabla\ $= Volum deplasement (m3), p = Tetthet (Tonn/m3), g = Tyngdeakselerasjonen(9,81 m/s2), ∆ = Vektdeplasement (Tonnes)
$\nabla$ × p = ∆
Formstabilitet: BM og vannlinjeplanet sitt treghetsmoment
Avstand BM (se figur 0201) beregnes etter formel: I/$\nabla\ $, I = vannlinjeplanets treghetsmoment (m4) (tverrskips), $\nabla$ = Volumdeplasement (m3). For et vannlinjeplan med rektangulært form (se figur 0204) så beregnes I = L × B3 /12, L = lengde (m). B= bredde (m). Treghetsmomentet oppgis i m4 og det forteller hvor vanskelig det er å krenge et skip, eller rettere sagt hvor vanskelig det er å rotere planet om senterlinjen. Ut av formel for I ser man at Bredden på vannlinjeplanet har stor betydning for I sin størrelse. For et skip med ordinær skrogform så beregnes I slik = (L × B3 /12 ) × k , hvor k er en koeffisient som er mindre enn 1.
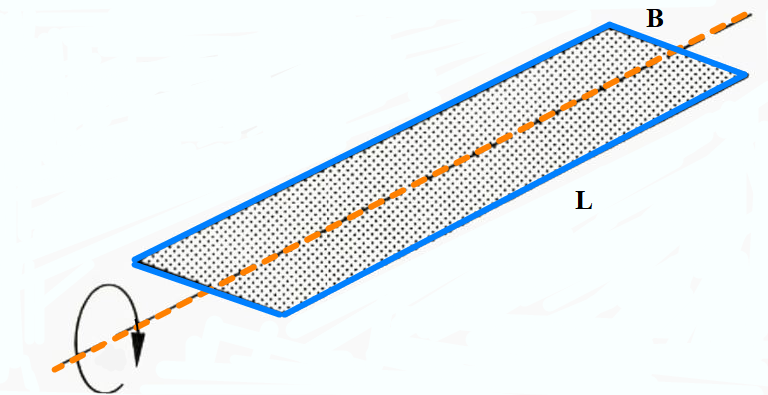
Figur 0204 Vannlinjeplan Treghetsmoment
Formstabilitet: KM.
For et skip med rektangulært form (pram) så beregnes KM slik = KB + BM, KB = T/2 (dypgående/2).
Enkel utledning av formel for tyngdepunkts forandring ved intern forflytning.

Figur 0205.
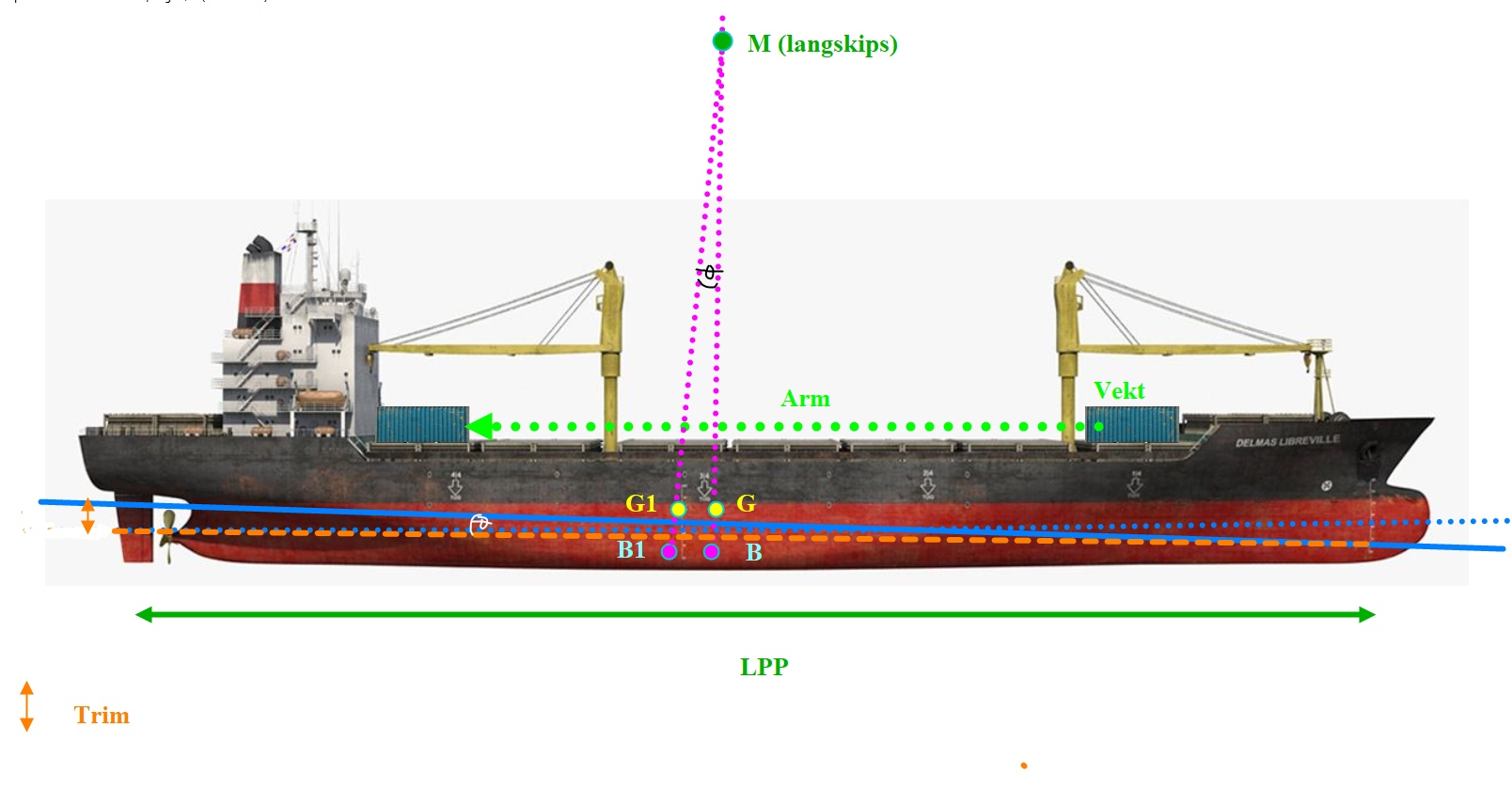
På et skip så blir det flyttet en container frem på dekk, g = opprinnelig plassering av tyngdepunkt til container og g1 er tyngdepunkt plassering etter forflytningen, begge tyngdepunktene blir flyttet i en avstand men ulike avstander (arm). G er skipets tyngdepunkt plassering før forflytningen og G1 etter forflytningen. Når man flytter containeren fremover dekk så vil det innvirke på skipets sitt tyngdepunkt. Det blir 2 momenter som er like stor, Moment 1 = Moment 2. Moment 1 = ∆ × GG1 og Moment 2 = Container vekt × gg1. Hvilke kjennskap har man til det som inngår i disse 2 momentene? Deplasementet skal til enhver tid være kjent for de ansvarlige om bord. vekten til containeren er oppgitt i manifestet, og avstanden som containeren blir flyttet finner man ut av ved hjelp av skipets plantegninger men GG1 lar seg ikke gjøre å finne i tabeller eller andre opplysningskilder.
Moment 1 = Moment 2
Vekt × arm = Vekt × arm
∆ × GG1 = container vekt × gg1, GG1 er ukjent, dividerer med ∆ på begge sider av likhetstegnet, slik at det er kun GG1 som står igjen på venstre side av likhetstegnet.
GG1 = Container vekt × gg1 / ∆, Container × gg1 blir Tonnmeter, dividerer med Tonnes og GG1 blir i meter.
De fleste formler innenfor stabilitet blir utledet slik som det blir gjort ovenfor.
En nærmere titt på Slakke tanker (fri væskeoverflate effekt) og GG2
Når en tank fylt som er fylt med væske ikke er helt full eller tom så vil den ha innvirkning på skipets tverrskipsstabilitet. Tverrskipsstabiliteten vil bli dårligere med at skipets tyngdepunkt G forflyttes vertikalt tilsynelatende til G2, med tilsynelatende menes at skipet oppfører seg som om at skipets tyngdepunkt G er i posisjon til G2, det eksakte tyngdepunktet vil i realiteten ikke befinne seg i G eller i G2 sine posisjoner slik som figur 0206 viser.
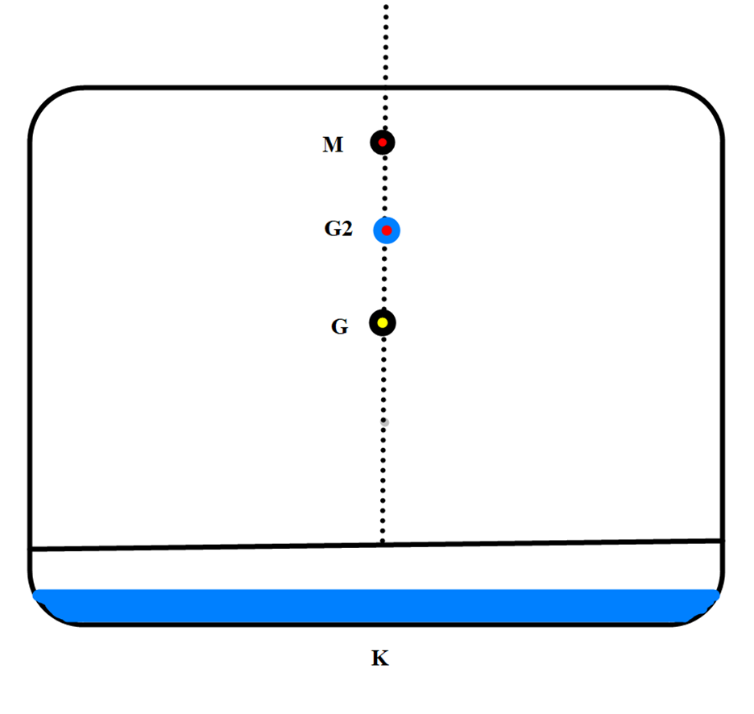
Figur 0206 Fri væskeoverflate effekt og GG2. Skipet sett akten ifra.
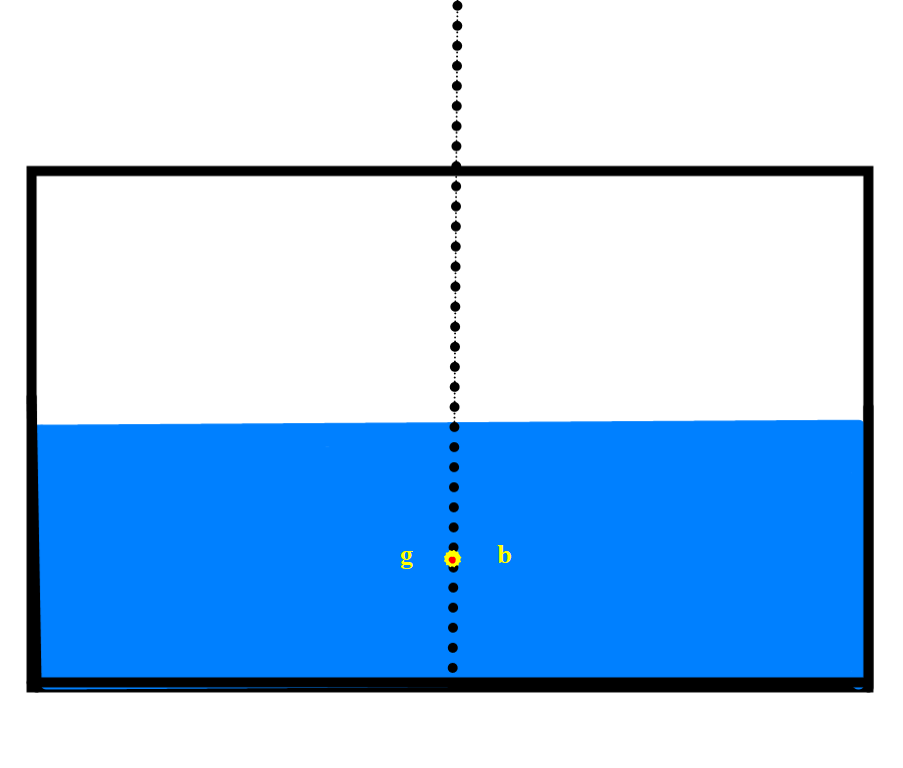
Figur 0207 En tank om bord i et skip som er halvfullt med væske.
En tank om bord i et skip som er halvfull av væske, sett akten ifra, tyngdepunkt (g) og oppdriftpunkt (b) blir i samme posisjon. Skal nå utlede en formel for fri væske overflate og GG2, der man benytter samme metode som ved utledning av GG1 og benytter formel for BM også (se lengre opp)
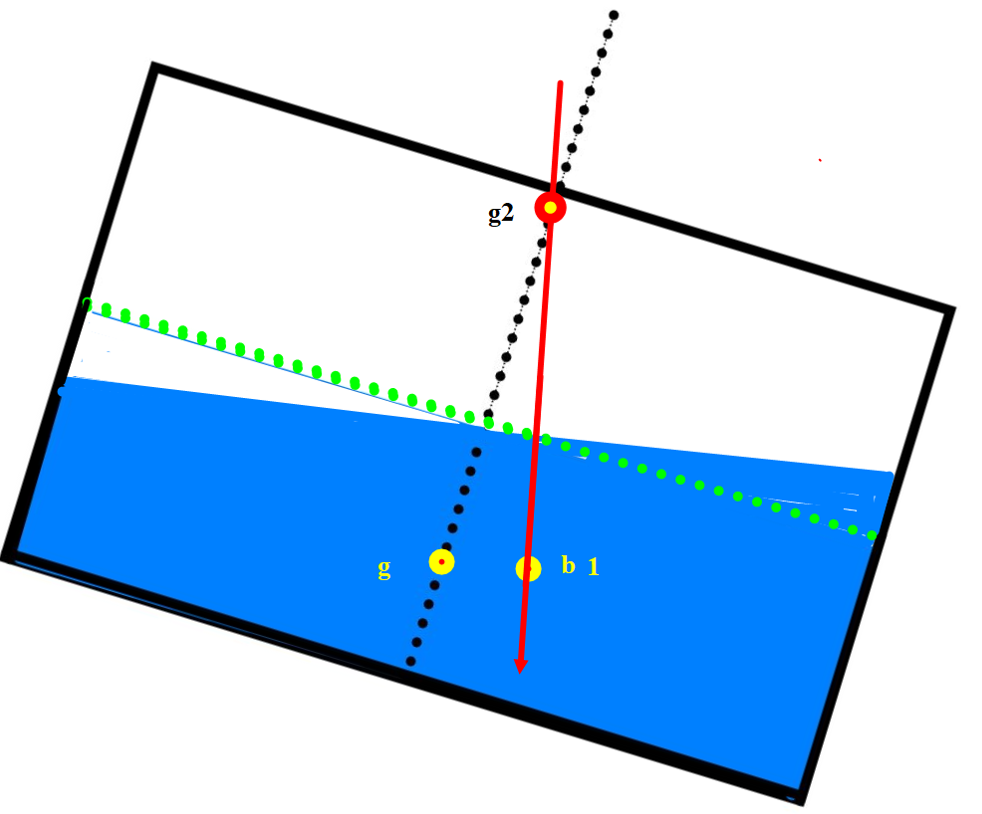
Figur 0208
Figur 0208 viser tanken med opprinnelig tyngdepunkt (g) og tilsynelatende tyngdepunkt (g2), lokalt for tanken. Den grønne stiplet linjen er der hvor væskelinjen er når tanken er uten krengning. Oppdriftpunktet b skifter posisjon til b1 på grunn av volumet har endret form, har hevet seg og flyttet seg til siden. I figur 0403 så virket oppdriftkraften fra B1 oppover men her virker tyngden av væsken i tanken i gjennom b1 nedover. Der hvor kraftlinjen skjærer senterlinjen for tanken vil bli posisjonen for g2, g2 blir et virtuell tyngdepunkt som medfører at tanken innvirkning på skipets stabilitet blir som om tyngdepunktet er i dette punktet.
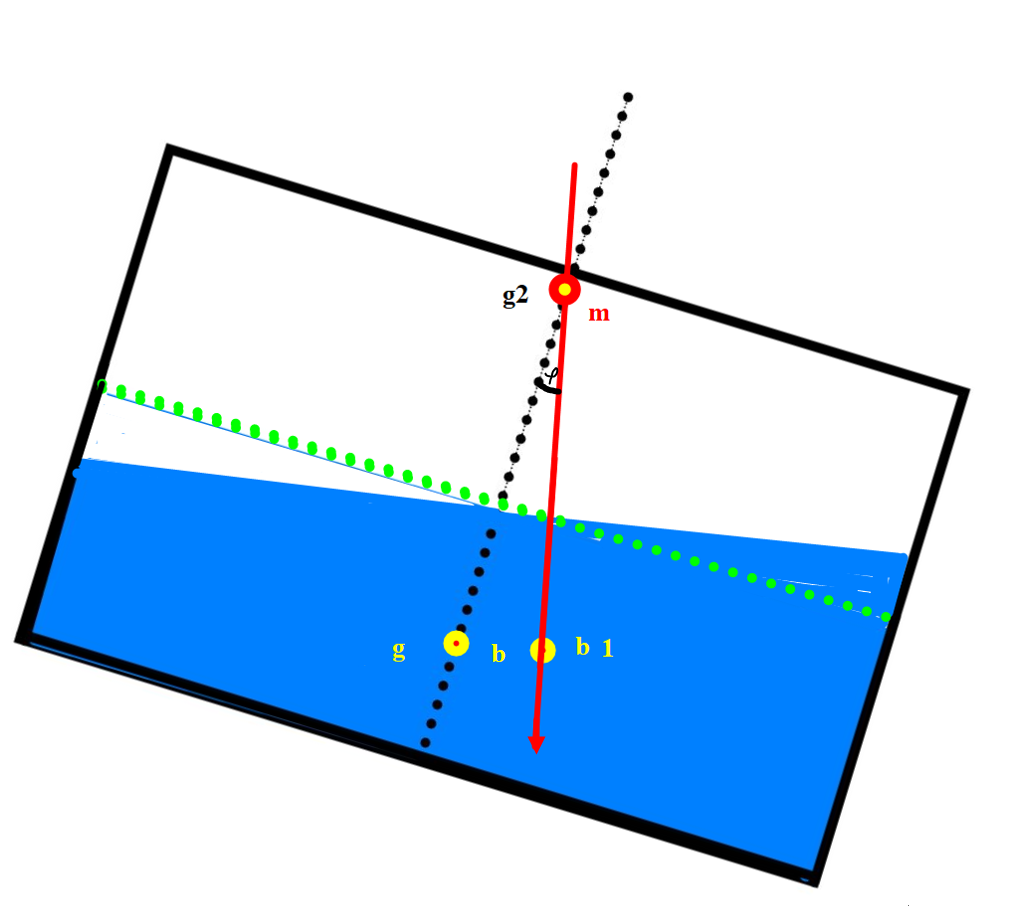
Figur 0209
Hva er kjent for de ansvarlige om bord i figur 0409? Aktuell volum og tyngdepunkt lar seg beregnes ut av skipets tabeller men for g2 er det ikke mulig. Fra skissen ser man at avstand gg2 = avstand bm. Formel for BM ved oppdrift= I/$\nabla$ . For tanken blir bm = i/volum væske, i (væskelinjeplanets treghetsmoment) beregnes etter den grønne stiplet linjen (L × B3/12), tanken har rektangulært form.
Figur 0210
Det er 2 momenter som inngår i skissen ovenfor, Moment 1= ∆ × GG2 og Moment 2 = Vekt (væske) × gg2, GG2 lar seg ikke gjøre å finne i skipets tabeller men gg2 lar seg beregnes.
Moment 1 = Moment 2
∆ × GG2 = vekt (væske) × gg2
∆ × GG2 = volum × p × gg2
∆ × GG2 = volum × p × gg2 (gg2 = bm)
∆ × GG2 = volum × p × bm (bm = i/volum)
∆ × GG2 = volum × p × i/volum (volum blir forkortet med volum)
∆ × GG2 = i × p
GG2 = i × p/∆
i = treghetsmomentet til overflaten (væskeplanet) i tanken om tyngdepunktet g2 (m4)
p = Væsken tetthet (tonn/m3)
∆ = Vektdeplasement (Tonnes)
i × p = Fri væskeoverflate effekt (Tonnmeter)
Metasentret(m) til tanken (g2) oppfører seg akkurat som metasentret til et skip, ved krengninger opp til 10 - 12° så vil det stå i ro (samme punkt) men ved større krengninger så vil det flytte på seg. Denne metoden er dermed korrekt opp til 10 - 12°, eller rettere sagt så tar denne «litt i». Et skip vil normalt krenge mindre enn 10 - 12° på en sjøreise Ved en krengning på 30° så blir effekten av fri væske overflate noe helt annet. Metoden tar ikke for seg krengendemoment , en halvfull tank vil ha størst innvirkning på stabiliteten.
Oppgave GG2
M/S Linda har ∆ = 18500 Tonnes, DB TANK No. 3 P/S er halvfull med sjøvann (inkludert i ∆).
a) Hva blir GG2?
b) Hva blir gg2?
Løsningsforslag:
Tar ut i for DB TANK No. 3 P/S = 2936,0 3 m4, p = 1,025 tonn/m3
a) GG2 = i × p/∆ = 2936,03 m4 × 1,025 tonn/m3 / 18500 Tonnes
GG2 = 0,162 meter
b) Bruker Moment 1 = Moment 2 som utgangspunkt
∆ × GG2 = vekt (væske) × gg2, vekt (ballast) = 672,4 Tonnes / 2 = 336,2 Tonnesvekt × gg2 = ∆ × GG2
gg2 = ∆ × GG2/ vekt
gg2 = 18500 Tonnes × 0,16 m/ 336,2 Tonnes
gg2 = 8,80 meter
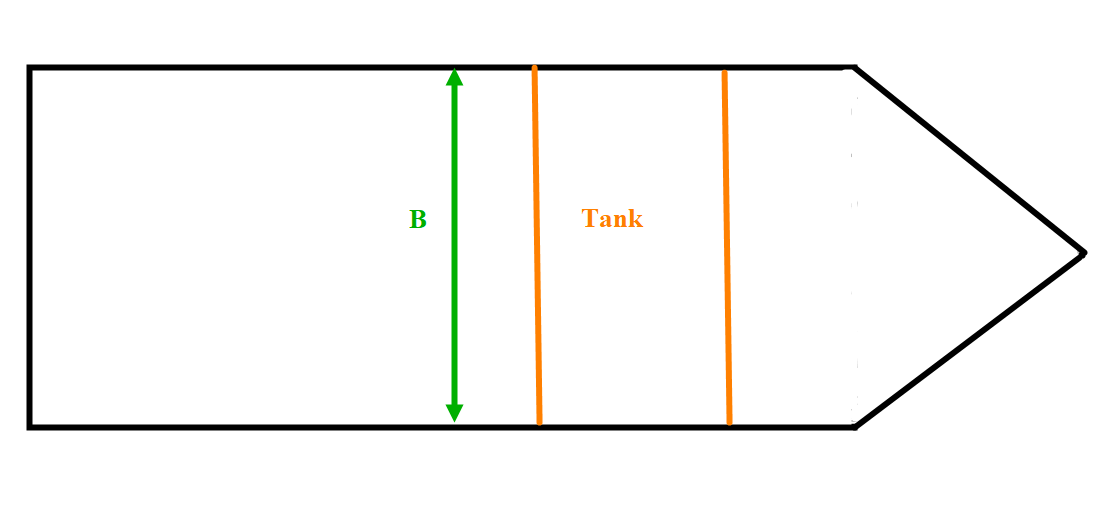
Reduksjon av fri væskeoverflate effekt med langskips skott i tanken
I for en tank = l × b3/12, (m4), ser av figur at tanken er like bredt som skipet. Det vil medføre en veldig stor I som vil redusere tverrskipsstabiliteten med GG2.
Figur 0211
Figur 0212
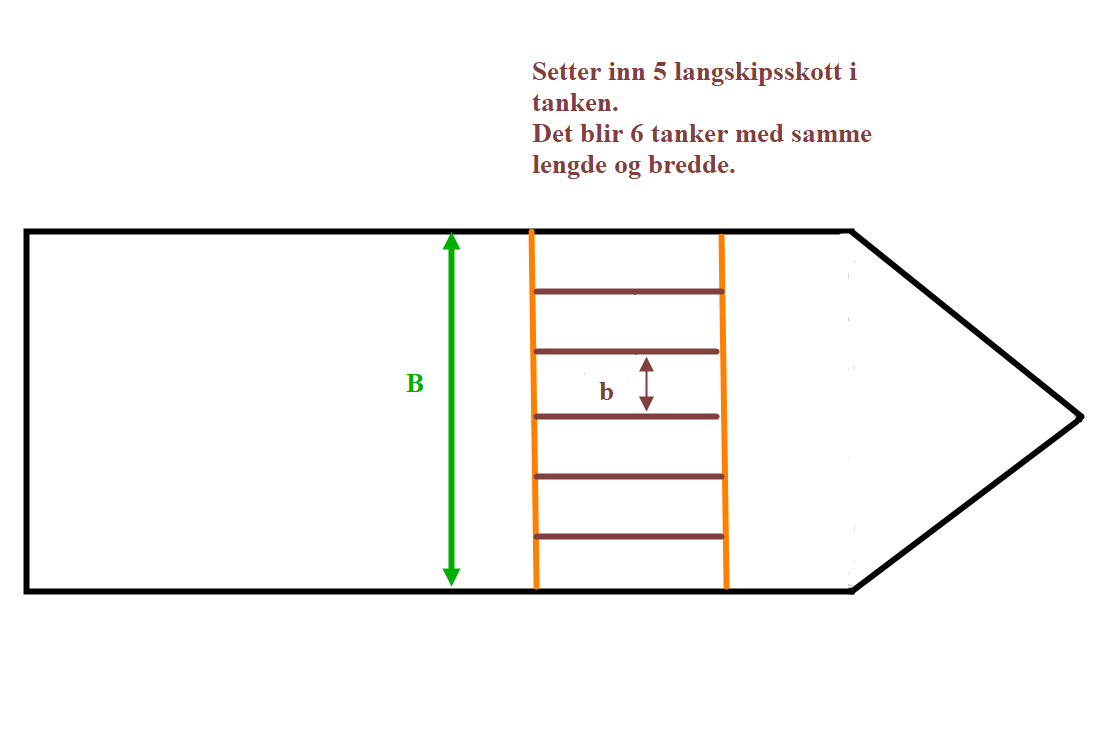
Samme tank får montert inn 5 langskipsskott, slik at det blir 6 tanker med samme bredde. b = B/6, hvis B = 12 m så er b = 2 m.
I for hver av de 6 tankene blir like stor. Total I for de 6 tankene vil bli: i × 6.
En generell utledning vil bli; Total treghetsmoment = i × n, n = antall tanker.
Treghetsmoment for 1 tank vil bli: i = (l × (B/n)3/ 12, → (l × B3)/12 × n3 (skiller teller og nevner men beholder samme potens både for teller og nevner)
Totale treghetsmomentet blir: (l × B3)/12 × n3 × n, forkorter med n
Totale treghetsmomentet blir: (l × B3)/12 × n2
Tanken(ene) lengde er 6 meter.
Hva blir treghetsmomentet når det er 1 tank?
Treghetsmoment = (l × B3/12 → 6 m × 12m3 /12 = 864 m4, b = B
Hva blir treghetsmomentet når det er 6 tanker?
Treghetsmoment = (l × B3)/12 × n2 → 6 m × 12m3 /12 × 62 = 24 m4 (redusert med 840 m4, som blir i prosent= 97 %), n × b = B
Det har ikke vært nødvendig å ta med et skip i utledningen, tanken i seg selv hadde holdt lenge nok, men skipet ble tatt med for å forenkle utledningen.
En nærmere titt på BM (forenklet utledning)
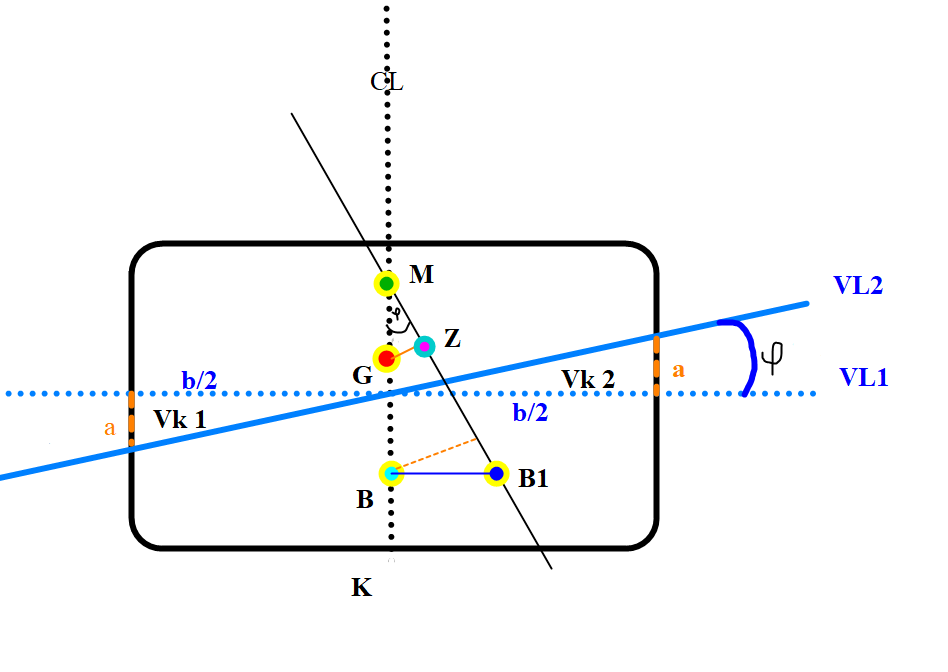
Figur 0213 Forenklet skisse av et skip som krenger
Her blir skipet tegnet uten krengevinkel og oppdriftkraften tegnet med krengning. VL1 er vannlinje 1 (uten krengning) og VL2 er vannlinje med krengning. Skipet krenger med vinkel $\varphi$ , som medfører to volumkiler, Vk1 og Vk2. Skipets bredde er b og skipets lengde l ( fremkommer ikke på skissen), vannlinjeplanet er rektangulært i sin form. Krengningen fra VL1 til VL2 medfører at B flytter seg til B1 (B1 skulle egentlig ha flyttet seg til hvor den oransje stiplete linjen ender på den svarte linjen, men det er også en del av forenklingen. Forskjellen vil ikke være så stor som skissen viser.)
Volumet til hver av kilene (areal trekant x l ) = (1/2 × b/2 × b/2 × tan $\varphi$ ) × l = (b2 × l)/8 × l × Tan $\varphi$.Tyngdepunktet til trekanten vil ligge 1/3 av b/2 fra skutesiden, og 1/3 av avstand mellom vannlinjene ( VL1 og VL2) som blir a/3. Volumet vil flytte seg fra tyngdepunktet i den ene volumkilen til tyngdepunktet i det andre , det blir en avstand på 2/3 b. Volummomentet (MV) blir volum × arm , arm blir 2/3 b. MV = Volum × arm = Volum × 2/3 b. (Volum til volumkilen = (b2 × l)/8 × l .
Volummoment1 = ((b2 × l)/8 × l × Tan $\varphi$ ) × 2/3 b = (m).
Det vil også være et Volummoment 2 ved at B flyttes til B1, $= \nabla$ × BB1 , Et enklere uttrykk for BB1 er gitt ved = BM × Tan $\text{φ }$, fordi Tan $\varphi$ =BB1 /BM.
Volummoment 1 = Volummoment 2
b3 × l /12 × Tan $\varphi$ = $\nabla$ × BB1
b3 × l /12 × Tan $\varphi$ = $\nabla$ × BM × Tan $\varphi$ , Tan$ \varphi$ forkortes på begge sider
b3 × l /12 = $\nabla$ × BM
BM = (b3 × l /12) /$\nabla$
BM = l × b3 /12 / $\nabla$
Ved betraktning av BM = l × b3 /12 / $\nabla$ , så kan $\nabla$ betraktes som konstant for denne tilstanden. Da ser man at det bredden som virkelig bidrar til BM sin størrelse, dermed kan man fastsette at bredden er viktig for skipets tverrskips stabilitet.
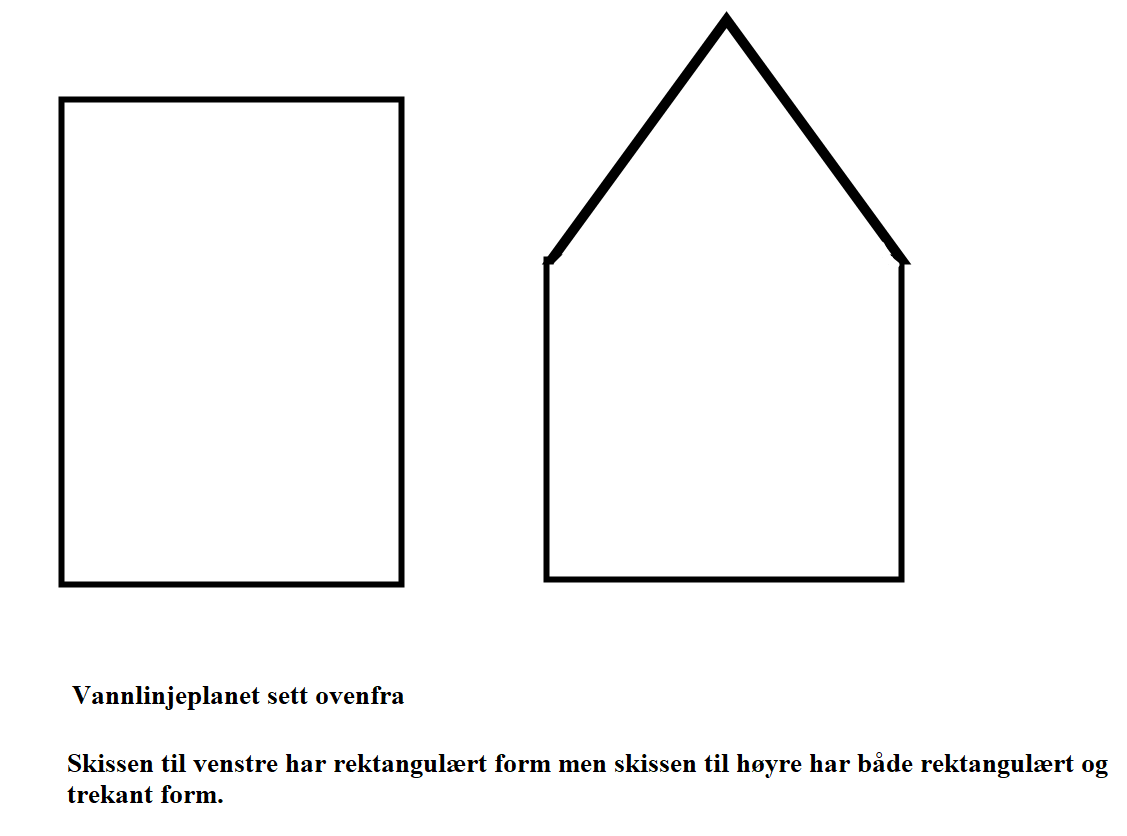
Figur 0214 Vannlinjeplan sett oven ifra
I utledningen til forenklet utledning av BM så er vannlinjeplanet til venstre benyttet og det gir ingen begrensinger ved utregning. Hvis vannlinjeplanet til høyre skulle ha vært benyttet så har det blitt avgrensinger på grunn av trekantform i tillegg til rektangulært form.
Formkoeffisienter, litt utvidet:
Prosjekt øket bredde: Stykkgodsskipet «Utgangspunkt Harmoni» vil bli benyttet som referanse når stykkgodsskipet «prosjekt 1» skal planlegges.
| Utgangspunkt Harmoni | Hoveddimensjoner |
|---|---|
| Deplasement | 17015 Tonnes |
| Lpp | 142 m |
| B | 18,60 m |
| Dybde i Riss | 11,75 m |
| T | 9,03 m |
| TPC | 22,10 Tonn pr cm |
Figur 0215 Skisse av «utgangspunkt Harmoni»
Første oppgave blir å beregne CB og CW.
CB = $\frac{\nabla}{L\ \times B\ \times \ T}$ =$\frac{16600\ m3}{142\ m\ \times \ 18,\ 60\ m\ \times \ 9,\ 03\ m }$ = 0,697 (-)
CW = $\frac{\text{AW}}{L\ \times B}$ men AW er ikke oppgitt? Hvordan kan man beregne CW da? Formel for TPC= $\frac{AW\ \times }{100}1,025\frac{\text{tonn}}{m3}$ , da vil et uttrykk for AW bli = $\ \frac{TPC\ \times \ 100 }{1,025\ tomnn/m3}$ = $\frac{\ 22,10\frac{\text{tonn}}{\text{cm}} \times \ 100 }{1,025\ tomnn/m3}$ = AW = 2156 m2
CW = $\frac{\text{AW}}{L\ \times B}$ = $\frac{2156\ m2 }{142\ m\ \times \ 18,\ 60\ m}$ = 0,817(-)
Srykkgodsskipet «prosjekt 1» skal øke sin lastekapasitet med omlag 30 %. LPP skal beholdes men det blir økning i Dybde i riss med 1,45 m og bredden med 2,8 m.
| Prosjekt 1 | Nye hoveddimensjoner |
|---|---|
| LPP | 142 m |
| B1 | 21,4 m |
| Dybde i Riss 1 | 13,2 m |
Bredden økes proporsjonalt overalt slik at CB blir uforandret og CW betraktes som det samme. På grunn av bredde økning vil T (dypgang) bli redusert (δ T).
Setter opp en ligning som betrakter volumendringen på begge sider av likhetstegnet. Økning i bredde i er 2,8 m/18,60 m = 0,15 (15,05 %)
δ T × L × B1 × CW = L × B × T × CB × δ B/B
δ T = T × CB × δ B / B1 × CW = 9,03 m × 0,697 (-) × 2,8 m / 21,4 m × 0,817 (-)
δ T = 1,00 m
TPC til Prosjekt 1 blir = 22,10 Tonn/cm × 21,4 m /18,60 m = 25,42 Tonn/cm.
Prosjekt 1: Det er antatt at vektøkningen blir på 800 Tonnes.
Hva blir T til Prosjekt1?
T Prosjekt1= T - δ T + 800 Tonnes/ TPC = 9,03 m - 1,00 m + 0,31 m = 8,34 m
| Prosjekt 1 | Hoveddimensjoner |
|---|---|
| Deplasement | 17815 Tonnes |
| Lpp | 142 m |
| B | 21,40 m |
| Dybde i Riss | 13,20 m |
| T | 8,34 m |
| TPC | 25,42 Tonn pr cm |
Hvis stykkgodsskip «Utgangspunkt Harmoni» gjorde 16 knop fart på sin prøvetur og det er ønskelig at «Prosjekt 1» skal også holde 16 knop så må det økes maskinkraften slik at denne blir lik økningen i slepehestekrefter ved 16 knop. (resultat i slepetank).
Trim

Figur 0216 definisjon av trim vist med blå vannlinje
Definisjon på trim er forskjell på dypgående forut og akterut. Trim deles inn i forlig og akterlig. Ved forlig trim er dypgående størst forut
Det er fire trimmomenter som det opereres med og de kan betegnes som:
Trimmoment (1): Vekt × arm
Trimmoment (2): ∆ × GG1
Trimmoment (3): ∆ × BG
Trimmoment (4): Trim × MTC
Fremgangsmåten blir som vist tidligere, setter to momenter imot hverandre:
Trimmoment (4) = Trimmoment (3)
Trim × MTC = ∆ × BG
Trim = ∆ × BG/ MTC
Trim kommer ut i dette tilfelle i cm fordi det deles på MTC (TM/cm). BG er forskjell i langskipsavstand mellom B (LCB) og G (LCG), LCB er oppgitt i ressurshefte ved 0 trim (Even keel) og LCG beregnes etter moment beregning, der LCG = Sum langskipsmoment/ ∆. Hvis LCB = LCG så er det 0 trim, Hvis LCG er større enn LCB så er det forlig BG, forlig BG gir forlig trim. Dette er en kunstig metode fordi LCB og LCB vil i virkeligheten være plassert over hverandre i samme avstand i fra aktreperpendikulær. Når man setter Trimmoment (4) = Trimmoment (1) så kommer svaret ut med en trimforskjell ($\delta$), og ikke en bestemt trim.
En nærmere titt på MTC.
MTC er TM/cm og det forteller hvor mye trimmoment det må til for å forandre trimmen med 1 cm.
Figur 0217 Utledning av enhetstrimmoment MTC.
Figur viser et bulkskip med fotmerker på forre og aktre perpendikulære, som lå uten trim (EK). Så blir en vekt (container) flyttet fra luke # 2 til luke # 7, som medfører at skipet får en akterlig trim. Det oppstår to formlike trekanter, bestemt av Trimvinkel $\theta$. Tan $\theta$ til de to trekantene = Trim / LPP og BB1/BM. Det blir utgangspunktet for utledningen av MTC.
Trim/LPP = BB1/BM , BB1 er ikke bare å finne ut av plansjer til skipet, men BB1 ≈ GG1.
Trim/LPP = GG1/BM , GG1 = vekt × arm/∆
Trim/LPP = (vekt × arm/∆)/BM , BM = I / $\nabla$ ( I langskips)
Trim/LPP = (vekt × arm/∆)/ I/$\nabla$ , ∆ = $\nabla \times$ p , to brøker gir omvendt dividend.
Trim/LPP = (vekt × arm / $\nabla$ × p ) × $\nabla$/I , $\nabla$ forkortes bort, blir 1
Trim/LPP = (vekt × arm/p) × 1/I
(vekt × arm/p) × 1/I = Trim/LPP , Vekt × arm er et trimmoment (trimmoment (1))Trimmoment = p × I × Trim /LPP , setter trim lik 1 cm = 0,01 m eller 1/100 m.
Trimmoment/cm = p × I × 0,01 / LPP , når trim blir 1 cm så vil trimmomentet = MTC
MTC = TM/cm
p = Tetthet (tonn/m3)
I = Treghetsmoment i vannlinjeplanet i langskipsretning om LCF (m4). I langskips for en pram = B × L3/12
LPP = Lengde mellom perpendikulærene, Forre Perpendikulære og aktre perpendikulære, (m)
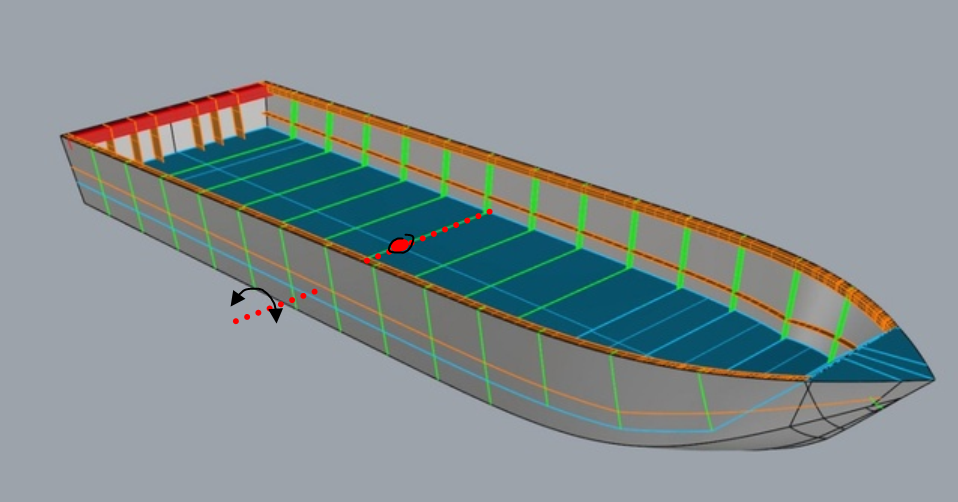
Figur 0218 LCF
LCF (longitudinal centre of flotation) Langskips flotasjonsenter. Det er et punkt i vannlinjeplanet som skipet vil dreie seg om, forover eller akterover, betegnes også som vannlinjeplanet sitt tyngdepunkt. På figur så er LCF tegnet inn med et rødt punkt og med en tverrskips akse som går i gjennom LCF punktet. Den lyse blå linjen på utsiden av skroget indikerer vannlinjeplanet beliggenhet. I = Treghetsmoment i vannlinjeplanet i langskipsretning om LCF (m4), treghetsmomentet forteller hvor vanskelig det er å få skipet til å rotere om den aksen som går i gjennom LCF punktet. I langskips, for et skip med normal skrogform, blir treghetsmoment = (B × L3/12) × k, k = faktor mindre enn 1, av formel ser man at det er lengden på skipet som bidrar mest, jo lengre skipet er jo vankeliger er det å trimme det.
Figur LCF betydning for dypgående
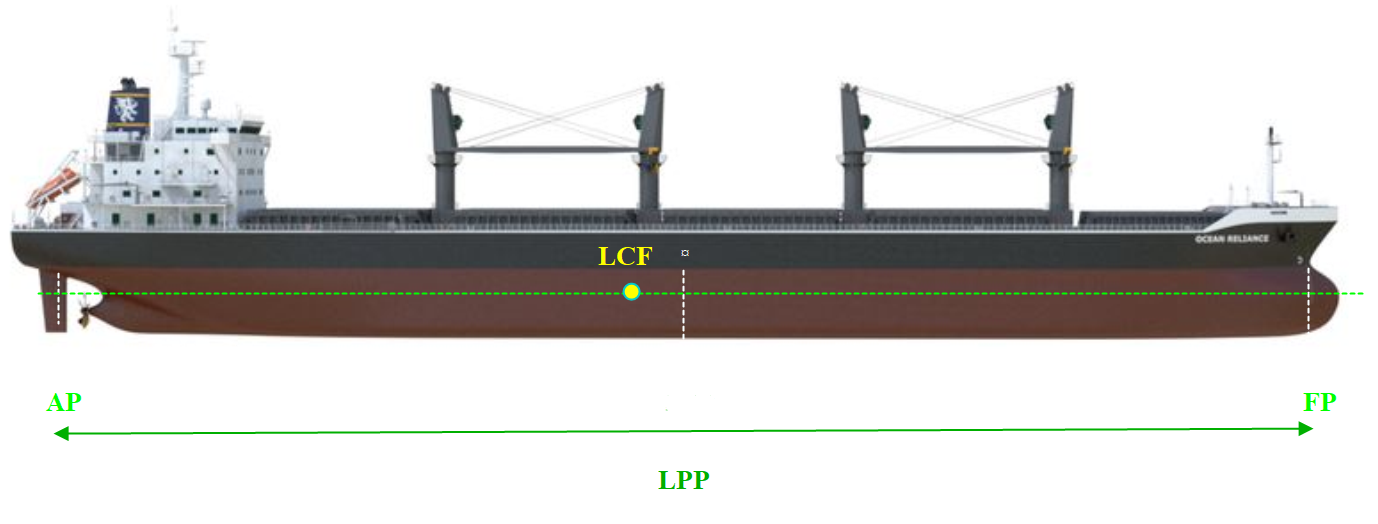
Figur 0219 LCF betydning for dypgående
Vises et bulkskip med LPP = 180 meter, fotmerkene er tegnet inn på: Forre perpendikulær, på ¤ (nullkrysspant) og på aktre perpendikulær. Den grønne stiplete linjen er et teoretisk vannlinjeplan, LCF til det vannlinjeplanet er 2,5 meter aktenfor ¤.
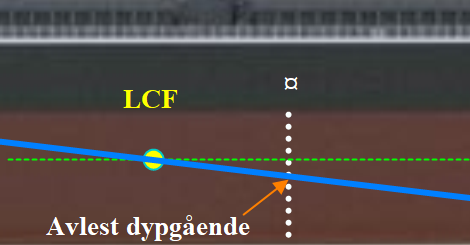
Figur 0220 LCF og beregning av dypgående
Hvis trim og skrogbøyning er lik null så vil den blå vannlinjen dekke over den grønne teoretiske linjen. Hvis det er trim så vil den blå vannlinjen være skilt i fra den grønne teoretiske linjen, men den vil krysse den grønne linjen i et punkt og det vil være i LCF (eller rettere sagt tverrskipsaksen til LCF).
Teoretisk dypgående vil være der den grønne stiplete linjen krysser fotmerket ved ¤ (nullkryss-spant), blir ofte kalt for referansedypgående. Avlestdypgående vil være der vannlinjen krysser fotmerket ved ¤, i dette tilfellet vil det være mindre enn referansedypgående. Den vertikale avstand i mellom dem lar seg beregne hvis man har kjennskap til LCF og trim. Den vertikale avstand kalles for trim korreksjon eller LCF korreksjon og betegnes som x.
Formel for x = trim × LCF/LPP, hvis trim i dette tilfelle var 3 meter akterlig så kan x beregnes, x = 3,0 m × 2,5 m /180 m = 0,04 m.
Referansedypgående er 12,0 meter, hentet i fra tabell til skipet på grunnlag av ∆ størrelse, og avlestdypgående blir: 12,0 m – 0,04 m = 11,96 m. Fotmerket ved ¤ er midt i mellom forre perpendikulær og aktre perpendikulær , og avlest dypgående forut og akterut lar seg beregne med å fordele halve trimmen forut og akterut.
| Avlest dypgående ¤ | 11,96 m | 11,96 m | ||
| Trim/2 | 01,50 m | 01,50 m | ||
| Avlest dypgående | Forut | 10,46 m | Akterut | 13,46 m |
Når man skal beregne fra avlestdypgående til referansedypgående: Trim beregnes ut av avlestdypgående forut og akterut, avlestdypgående ¤ = avlestdypgående forut + avlestdypgående akterut / 2. Vannlinjen tegnes inn med sin trim (forlig eller akterlig), mindre muligheter for å gjøre feil hvis man tegner styrbord siden hver gang, da blir baug alltid til høyre. Ved avlestdypgående ¤ tar man ut LCF verdien og tegner den inn på vannlinjen forlig eller akterlig (i forhold til fotmerket ved ¤).
Når LCF er tegnet inn så faller resten av brikkene fort på plass. Referansedypgående vil alltid være på en horisontal linje som går i gjennom LCF og der hvor den krysser fotmerket ved ¤ er referansedypgående. Trimkorreksjon x beregnes som ovenfor og det vil fremgå ut av skissen om den skal legges til avlestdypgående ¤ eller om den skal trekkes ifra.
En nærmere titt på GZ
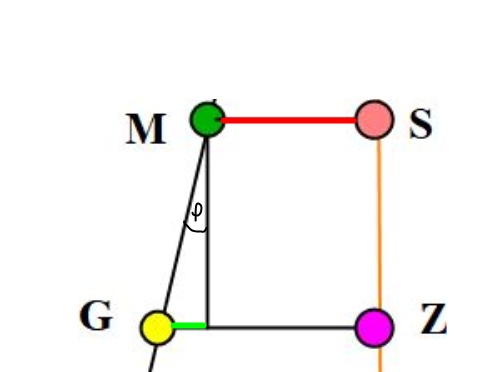
Figur 0221 Grunnskisse av GZ
Begynnelse stabilitet: Regnes når krengningsvinkel $\varphi$ er under 12°, da står metasentre i samme punkt og oppdriftkraften går i gjennom det. Hva skjer når krengningsvinkel $\varphi$ blir større enn 12°? Ved utledning av BM så man at bredden av vannlinjeplanet er viktig for stabiliteten. Større bredde gir bedre stabilitet , når krengningsvinkel $\varphi$ blir større enn 12° så økes bredden i vannlinjeplanet. Den økes helt til dekkshjørnet kommer i vannet og metasentre vil bevege seg høyere opp på senterlinjen, helt til dekkshjørnet kommer i vannet og da avtar den, forandrer retning og kommer nedover mot B1. Når metasentre flytter på seg så kan ikke formel for GZ = GM × sin $\varphi$ benyttes.
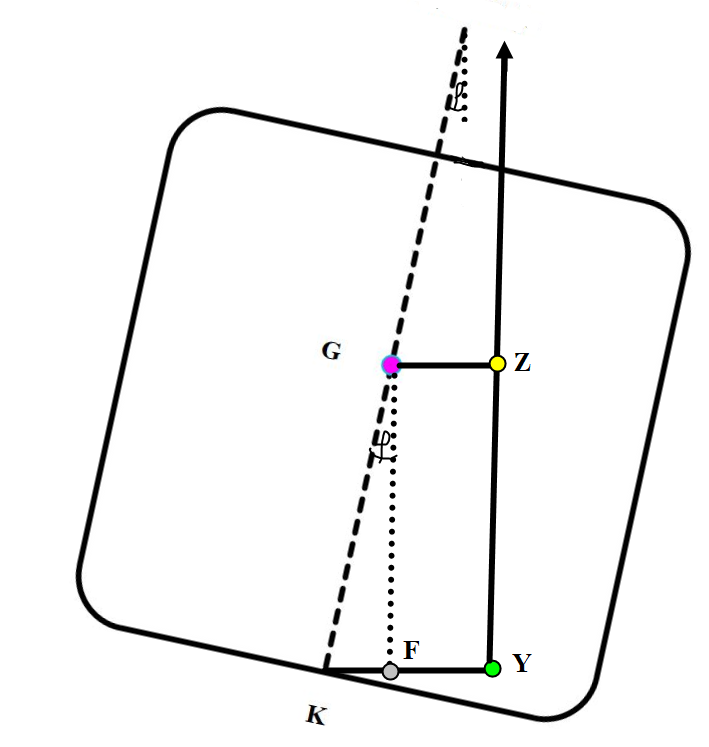
Figur 0222 Beregne GZ ved av KY (kurve)
Arm KY ble beregnet tidligere i fra en integrator, er et instrument, som med en bestemt krengningsvinkel for en modell av skipets skrog så ble det beregnet spantareal og arealmoment, volumdeplasement og Volummoment om en integratorakse. Når en kjenner Volummoment og volum, kan man finne volumets tyngdepunkt ved hjelp av avstand i fra intergratoraksen. Armen KY, er vinkelrett, vil forandre seg med forskjellige krengningsvinkler og ved forskjellige volumdeplasement. Oppdriftkraften er tegnet fra Y, men oppdriftpunkt B1 er mellom Y og Z en plass og er ikke tegnet inn. Der oppdriftkraften krysser senterlinjen vil ikke være metasentre men det falske metasentre (M~F~). Det er tegnet inn en hjelpelinje fra G loddrett på KY armen, der den treffer KY armen betegnes som F.
Ved hjelp av F kan GZ armen beregnes, fra figur ser man at GZ = FY, FY = KY -- KF. KF er motstående katet til krengningsvinkel $\varphi$ , Sin $\varphi$ = KF/KG → KF = KG × Sin $\varphi$. FY = KY -- KG × Sin $\varphi$. FY = GZ = KY -- KG × Sin $\varphi$. For et gitt deplasement og KG er GZ ved en gitt $\text{φ }$ → GZ (30°) = KY (30°) -- KG × Sin 30°.

Figur 0223 Bilde av Saga Odyssey.
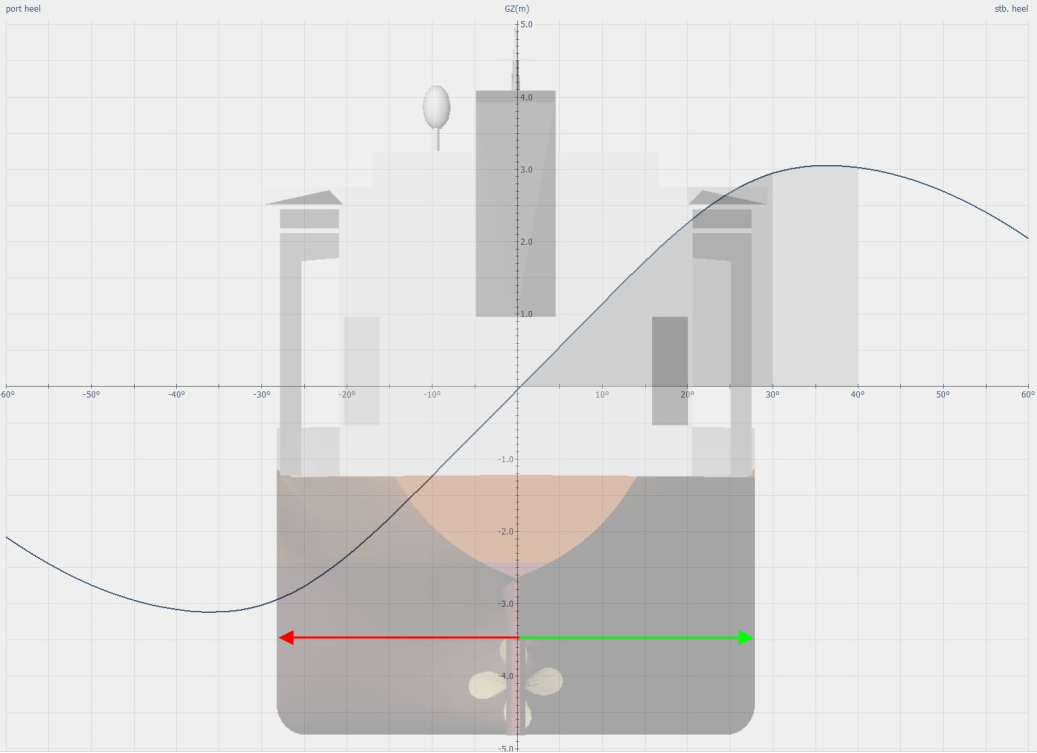
Figur 0224 GZ kurver til Saga Odyssey
Figur 0224 viser GZ kurver til Saga Odyssey Skissen viser skipet sett akten ifra, her ser man hekken og undervannsskrog, litt av overbygningen med skorstein og satellitt-doom, og de ytterste deler av Gantry kranene. Det er GZ kurve til babord og til styrbord, helt like men de er speilvendt av hverandre. På skissen ser man det er tegnet inn to piler, en til styrbord side og en til babord side, begge er tegnet ut i fra senterlinjen. De er nøyaktig like stor og er da symmetrisk om senterlinjen. Man ser av skissen at skipet er symmetrisk om senterlinjen helt opp til skorsteinen.
Når skipet er symmetrisk om senterlinjen så trenger man bare å tegne en GZ kurve, normalt til styrbord side.
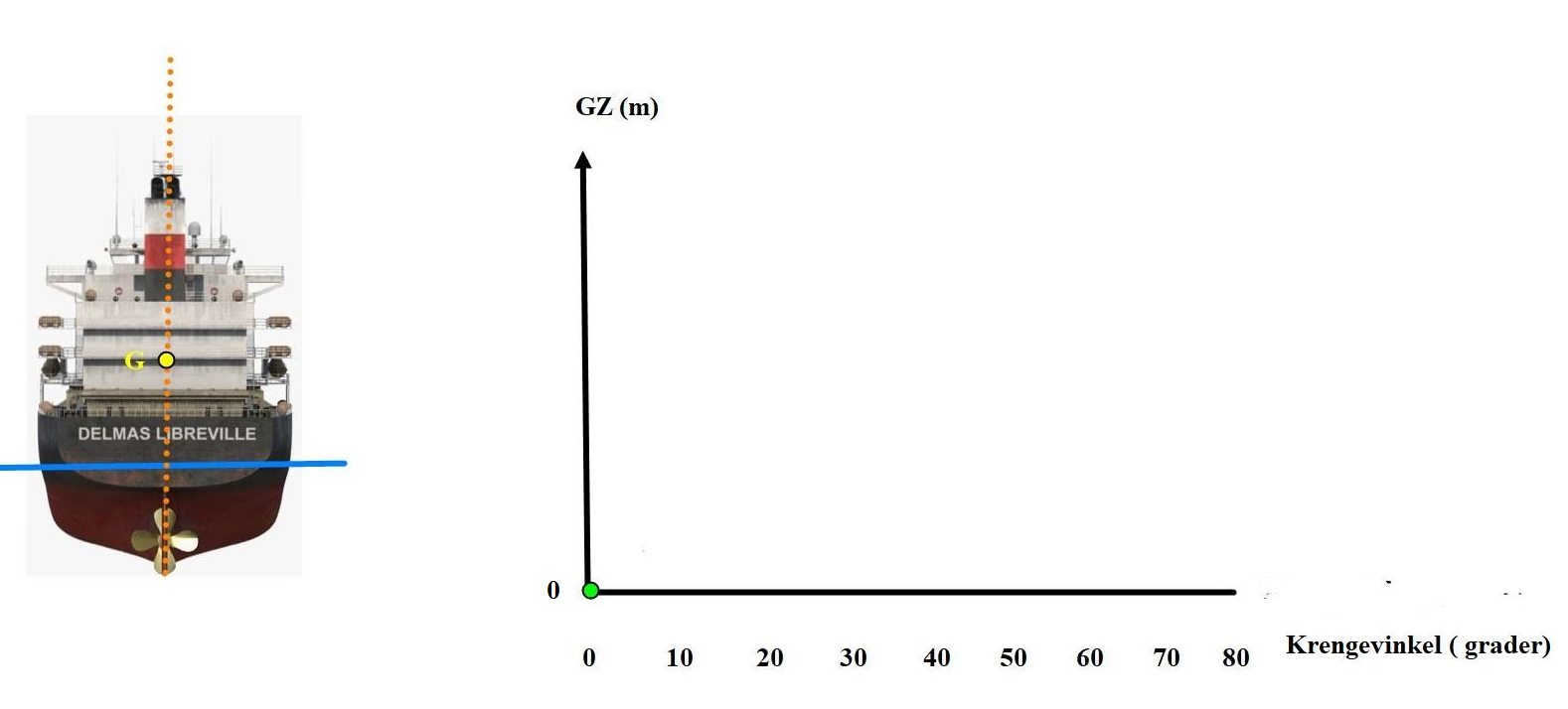
Figur 0225 Skipet er oppreist, 0 grader krengning og dermed er GZ (arm)= 0.
Figur 0226
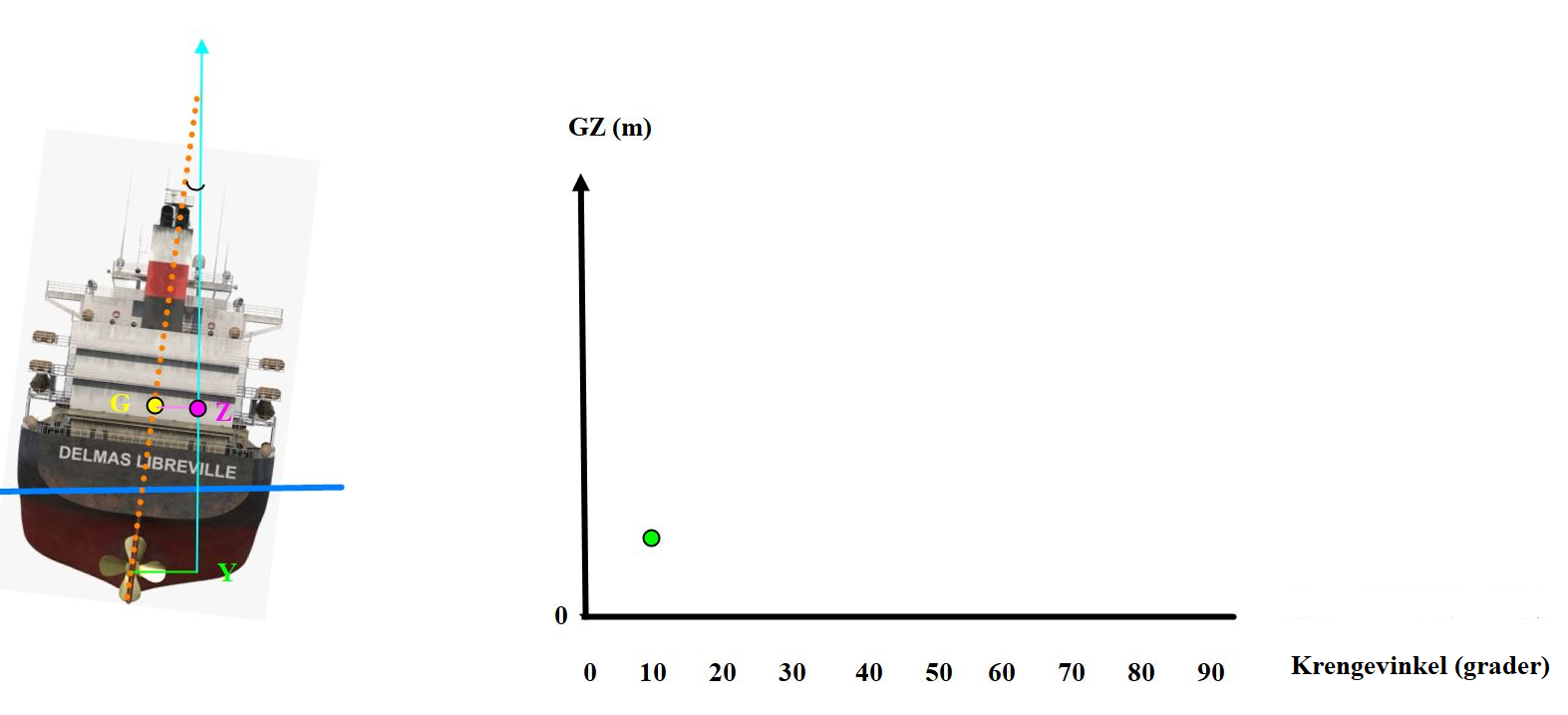
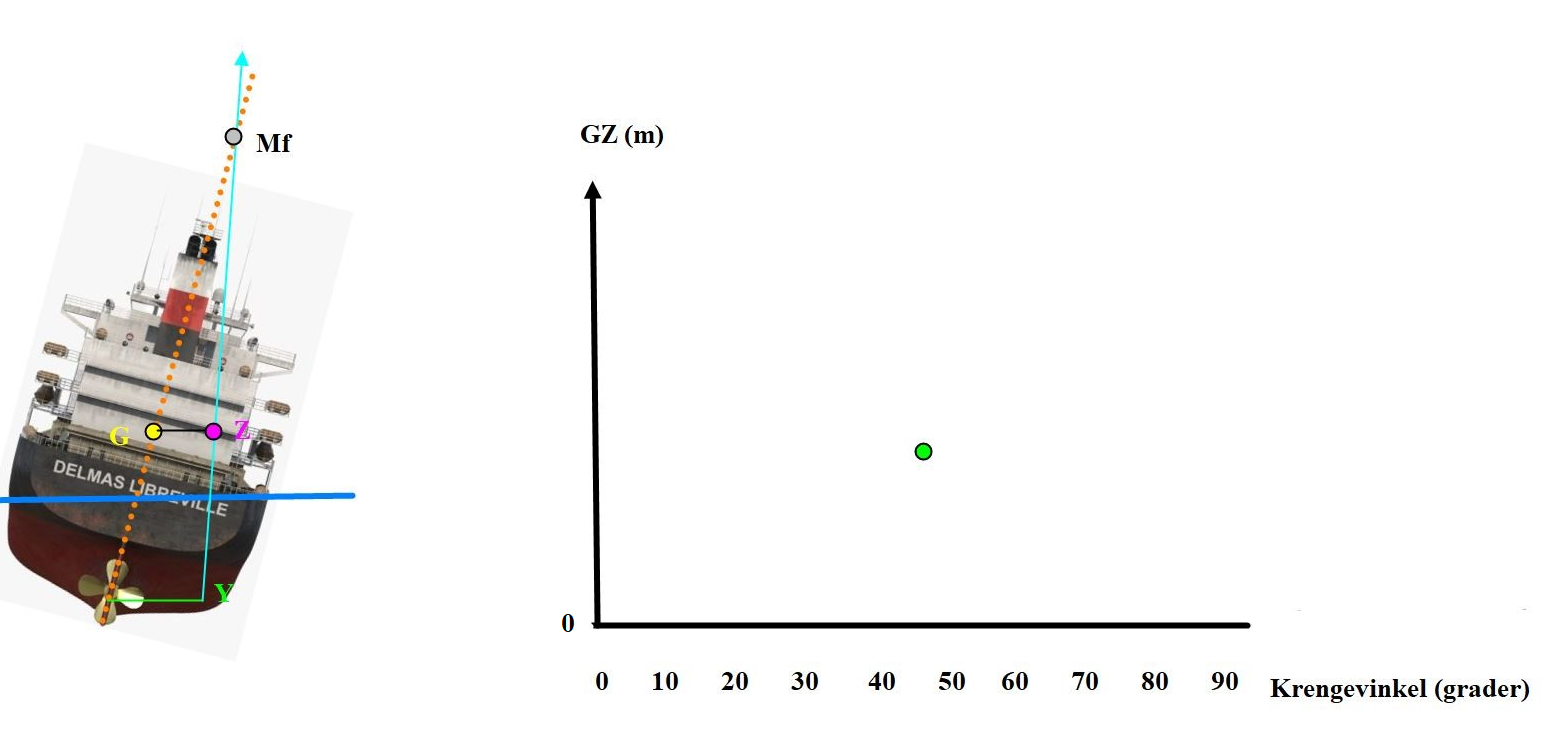
Figur 0226. Skipet har en krengning på 10 grade til styrbord. GZ er tegnet med en verdi, referansepunkt til GZ verdi er den horisontale linjen under hvor GZ er = 0.På skipet er GZ armen tegnet i horisontal retning men i diagrammet er den tegnet i vertikal retning. Her blir GZ som y og krengevinkel blir som x. Det grønne rundingen blir punktet i koordinatsystemet, som er beregnet etter formel i figur 0222.
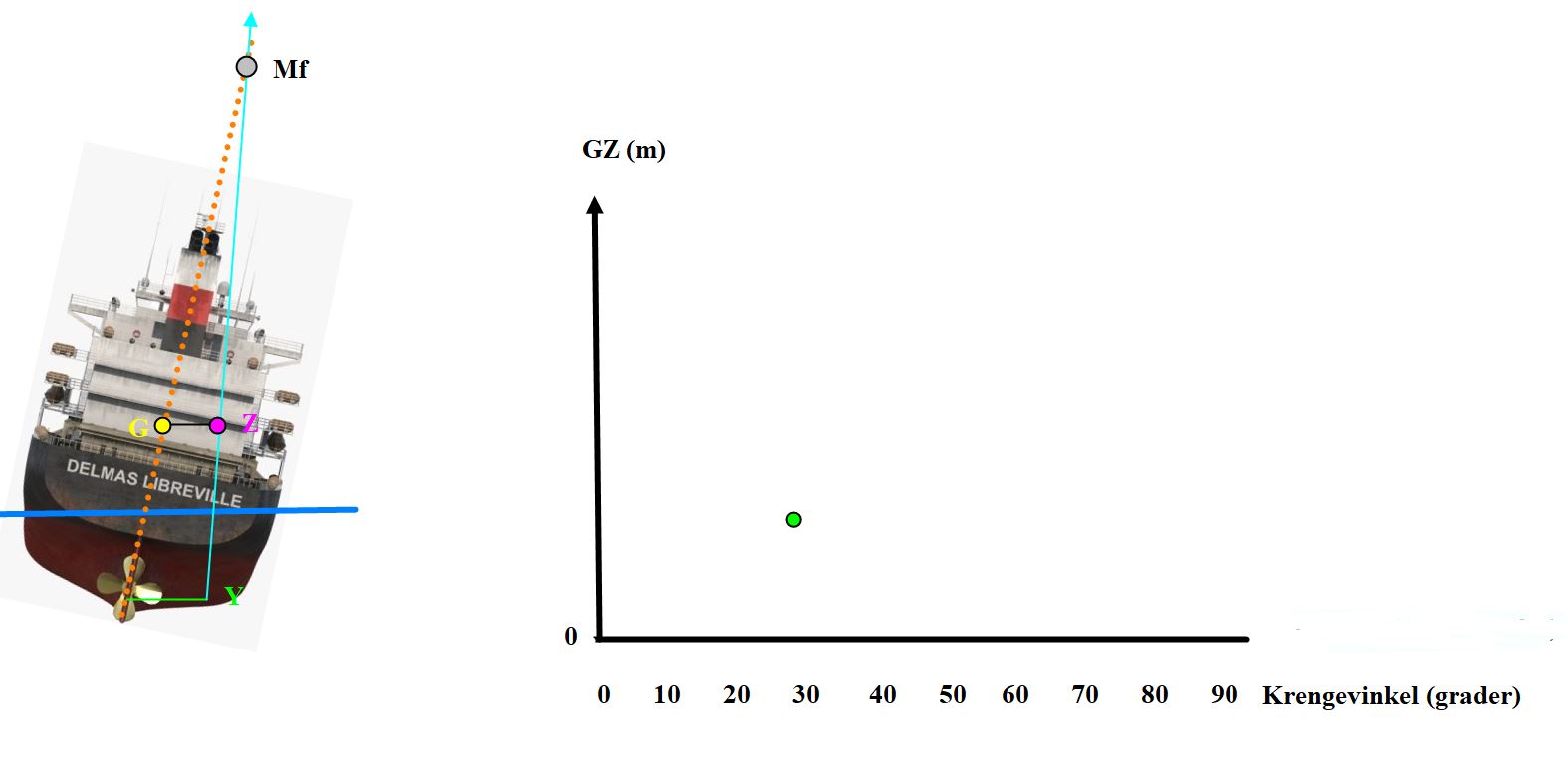
Figur 0227 Skipet har en krengning på 30 grader til styrbord, GZ øker med større krengning.
Figur 0228 Skipet har 45 grader krengning til styrbord, dekkshjørnet er i vannet og da er bredden i vannlinjen størst. I dette punktet vil GZ (maksimum) være på sin største verdi.
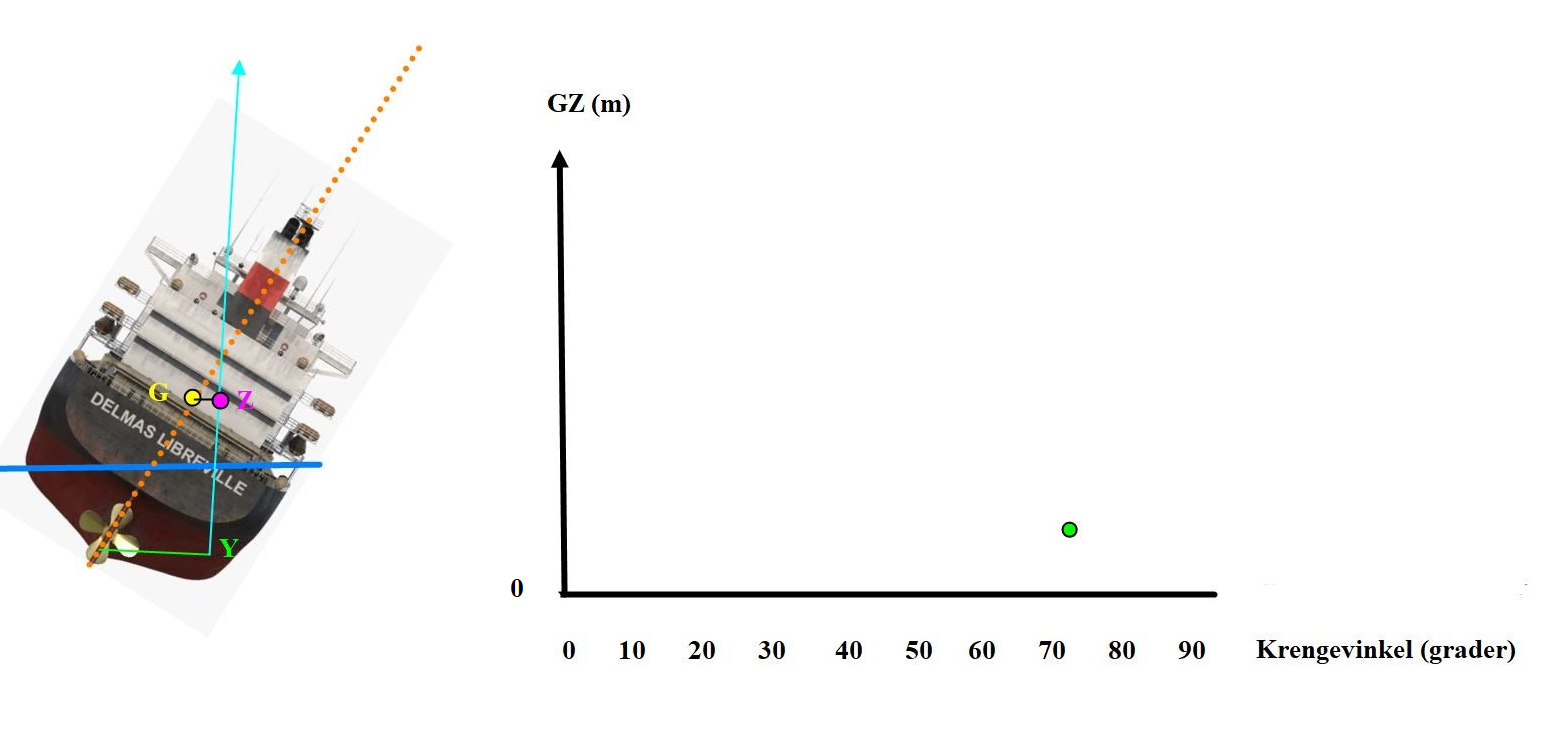
Figur 0229 Skipet har om lag 70 grader krengning til styrbord, bredden i vannlinjeplanet har avtatt og GZ verdien er mindre.
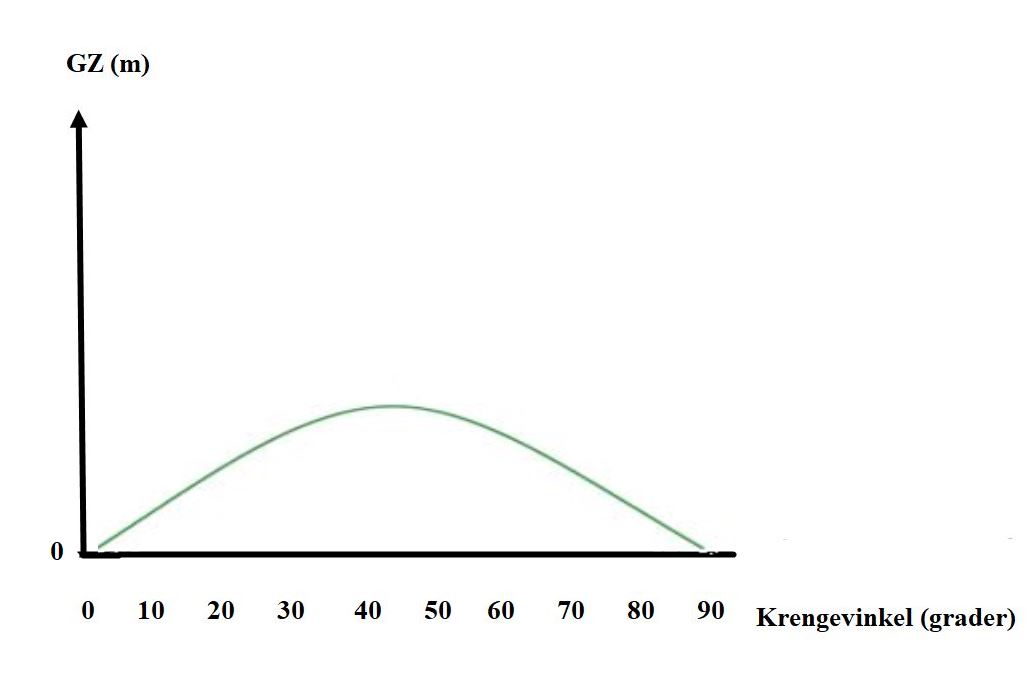
Figur 0230 GZ kurve. Det er tegnet en grønn strek i gjennom alle de grønne punktene som er angitt ovenfor, resultatet blir en komplett GZ kurve.
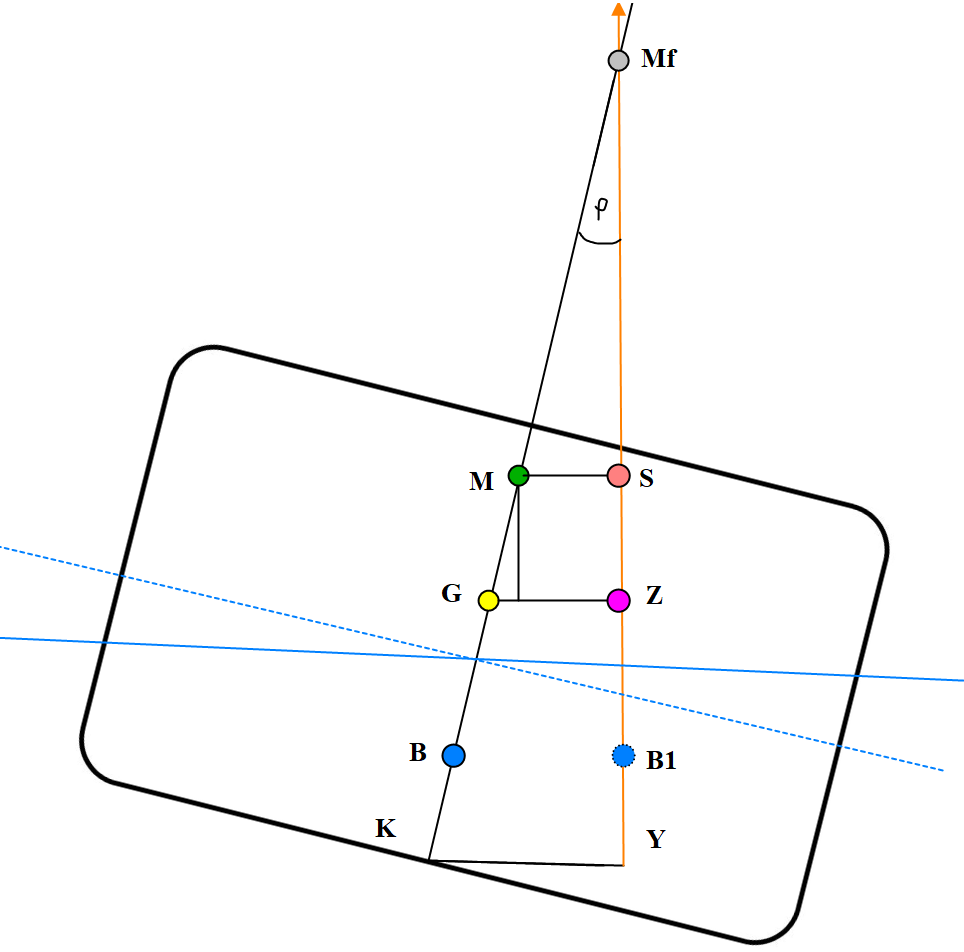
Figur 0231 komplett skisse av GZ
Skissen viser alle begrepene som er gjennomgått i tverrskipstabilitet. Her er M (metasentre til begynnelse stabilitet (initial)) tatt med, krengevinkelen er større enn 12° og der hvor oppdriftkraften skjærer senterlinjen er Mf (metasentre falsk). Avstand MS kalles for reststabiliteten, den økes med krengevinkel. I (tverrskips) økes med bredden, helt til dekkshjørnet er i vannet, det samme vil skje med MS som vil oppnå maksimumsverdi når dekkshjørnet kommer i vannet. Total stabiliteten = Begynnelse stabilitet(initial) + reststabilitet og den vil bli uttrykt ved hjelp av en GZ kurve.
Figur 0232 MS og beregning av GZ
Av figur ser man at GZ = motstående katet til GM trekant + avstand MS. Sin $\varphi$ = motstående katet (lys grønn)/ GM → Motstående katet = GM × Sin $\varphi$.
MS tas ut i fra tabeller til skipet ved ∆ og krengevinkel. Skipet «Mercandian Importer» beregner GZ ved denne metoden, her blir MS betegnet som M0s.
Totalstabilitet ved en bestemt krengevinkel $\varphi$ vil bli : GZ ($\varphi$) = GM × Sin $\varphi$ + MS ($\varphi$). For skipet «Linda» beregnes totalstabiliteten slik : GZ ($\varphi$) = KY($\varphi$) -- KG × Sin $\varphi$.
Reststabiliteten fremstår ikke så tydelig som den gjør på skipet «Mercandian Importer». Ved å forlenge den vertikale linjen fra metasentret helt ned til linjen KY, som blir punkt R og reststabiliteten til «Linda» blir RY.
RY = KY – KM × Sin $\varphi$ ( se figur 0233)
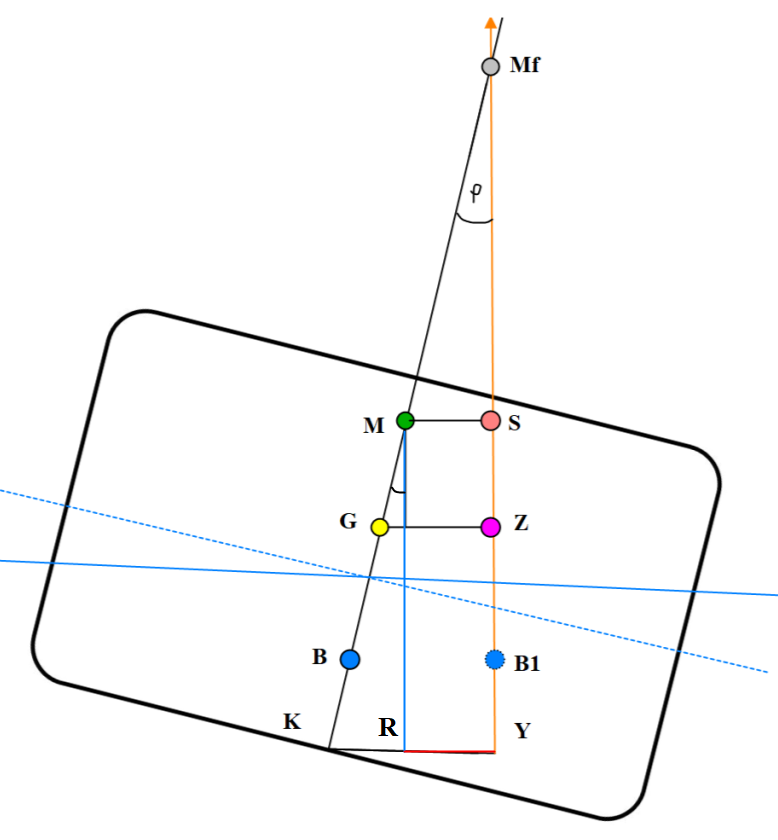
Figur 0233 Reststabilitet for Linda.
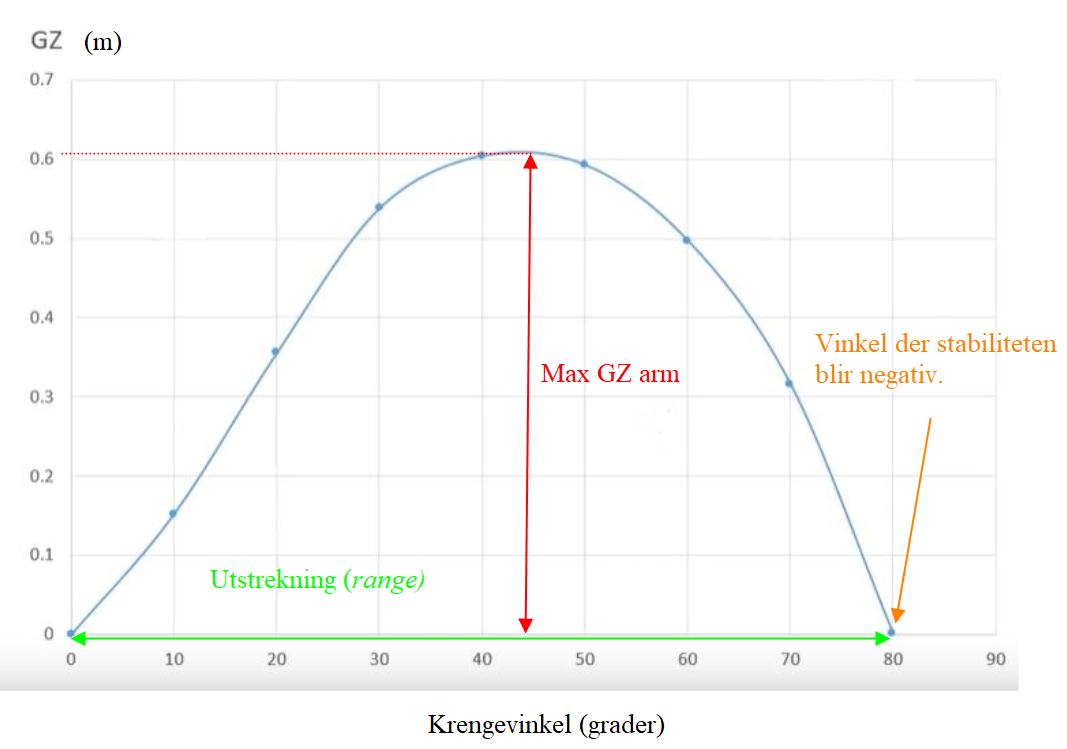
Figur 0234 Grunnleggende betegnelser for GZ kurver.
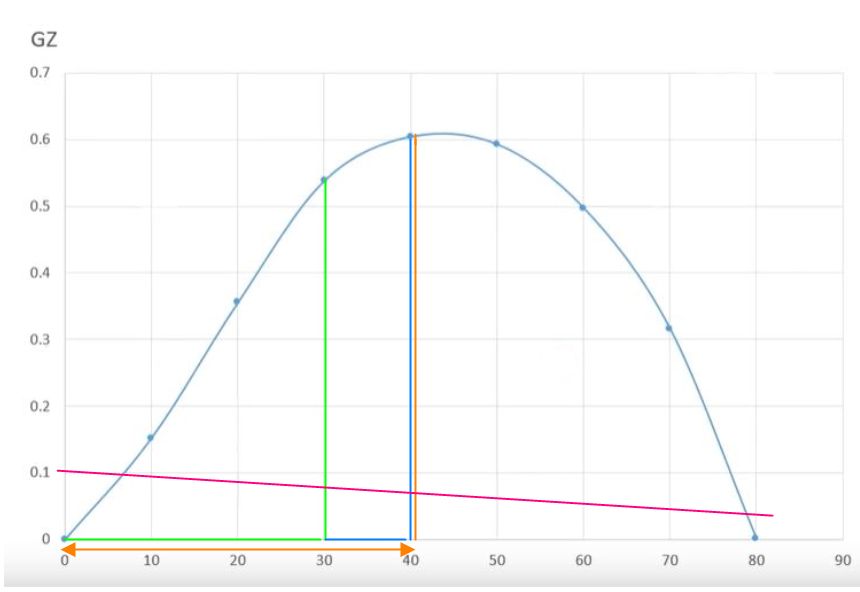
Utfra GZ kurven ser man: Utstrekning (Engelsk range), er rekkevidden til kurven der den har positiv stabilitet. Her er utstrekningen 80 ° (oppgis 0 – 80 °), ved 80 grader vil også GZ kurven bli negativ. GZ maks er der hvor GZ armen har størst verdi, her er den 0,62 m ved 45°.
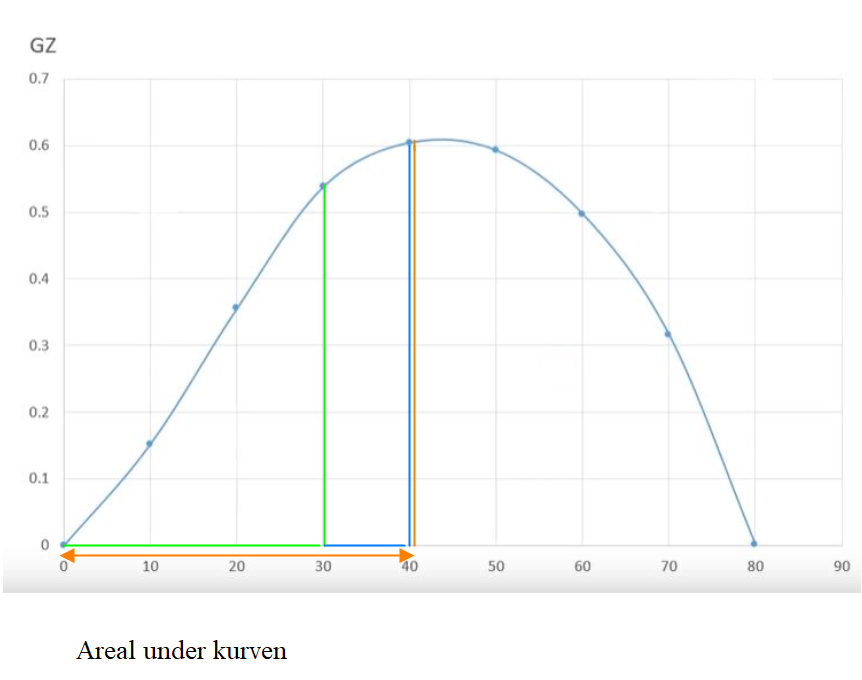
Figur 0235 areal til GZ kurven
Det er krav til areal under GZ kurven: ved 0-30°, 30-40° og 0-40°.
Krav til arealets størrelse: 0-30°= 0,055 meterradianer, 30-40°=0,03 meterradianer og 0-40° = 0,09 meterradianer.
GZ kurven er konstruert med hjelp av grader og meter, arealet fremkommer først i meter × grader = metergrader, men omgjøres til meterradianer. Arealkravene til GZ kurven stammer i fra forskningen som en Finsk professor J. Rahola foretok seg i 1937 – 1939, Rahola anbefalinger til GM og GZ areal er stort sett tatt til følge av de fleste sjøfartsnasjoner
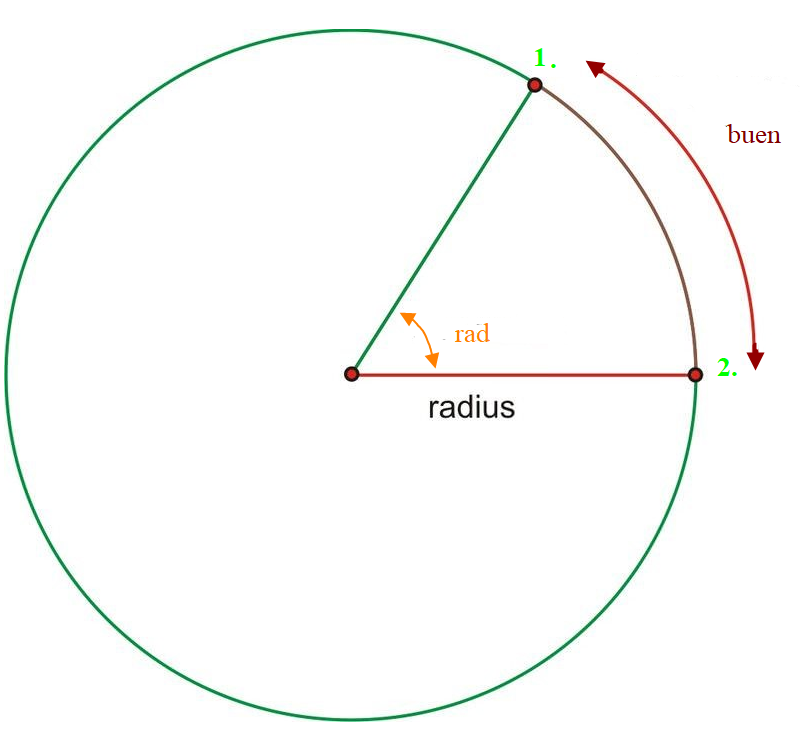
Figur 0236 Sirkelbue med vinkel i Radianer
Hvis man setter en passer med en fot på punkt 1., stiller den inn slik at den berører sentrum i sirkelen, og merker av et punkt på omkretsen (2.). Da vil vinkelbuen og radius være like stor og vinkelen vil bli 1 Rad (Rad er en forkortning av radianer).
Omkretsen til en sirkel er 360 ° , i Rad : 2$\text{π Rad }$.
Setter man at disse to er lik: 360 ° = 2$\text{π Rad}$ → Rad = 360° / 2$\text{π }$= 180°/$\pi$≈ 57,3°. 1 Rad er = 57,3° og 1 grad = 1 /57,3° = 0,01745 rad/grad.. 3,50 metergrader vil da bli: 3,50 metergrader × 0,01745 rad/grader, grader blir forkortet bort, dermed blir uttrykket = 0,61 meterradianer. Hvorfor beregne i meterradianer? Før i tiden var det vanlig å oppgi størrelser i eksaktverdi, på den tiden var det ikke kalkulatorer. Hvis man på en matematikkprøve ikke oppga svarene i eksakt verdier (trigonometriske) så kunne man oppnå å få null poeng.
beregne i meterradianer? Før i tiden var det vanlig å oppgi størrelser i eksaktverdi, på den tiden var det ikke kalkulatorer. Hvis man på en matematikkprøve ikke oppga svarene i eksakt verdier (trigonometriske) så kunne man oppnå å få null poeng.
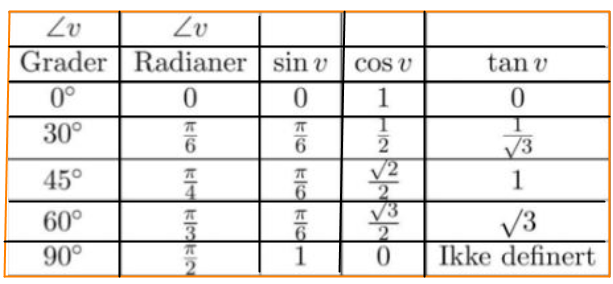
Figur 0237 Tabell for eksaktverdier
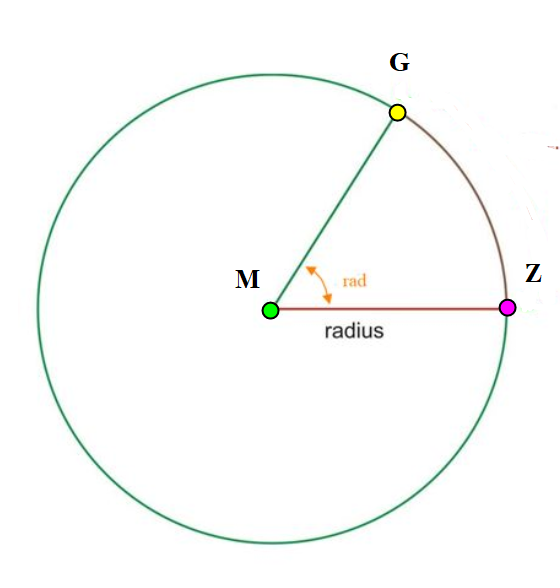
Figur 0238 Sirkelbue hvor skipets G, M og Z er tegnet inn.
Hvis vinkelen er 0 så vil GZ bli 0 men avstand GM vil bestå. Hvis vinkelen er 1 Rad så vil GZ og GM være like stor. Dette kan man dra nytte av se figur 0239.
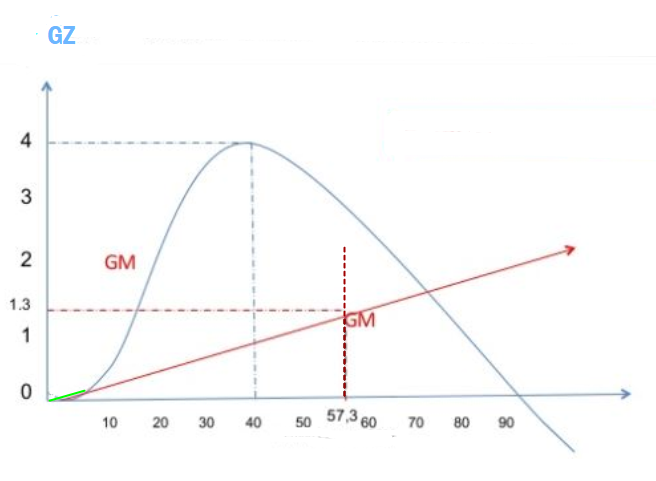
Figur 0239 bestemme størrelsen på GM ved en ukjent GZ kurve.
Vinkel 1 Rad ≈ 57,3 °. Hvis man kommer over en GZ kurve, der man ikke kjenner til GM, så kan man ved hjelp av GZ kurven finne det ut. Tegner en linje som tangerer GZ kurven fra 0 – 5 °, ved 57,3 ° tegner man en vertikal linje og der hvor tangentlinjen og den vertikale linje skjærer hverandre vil være punktet til GM. GM leses av på den vertikale GZ, i dette tilfelle er den 1,3 meter.
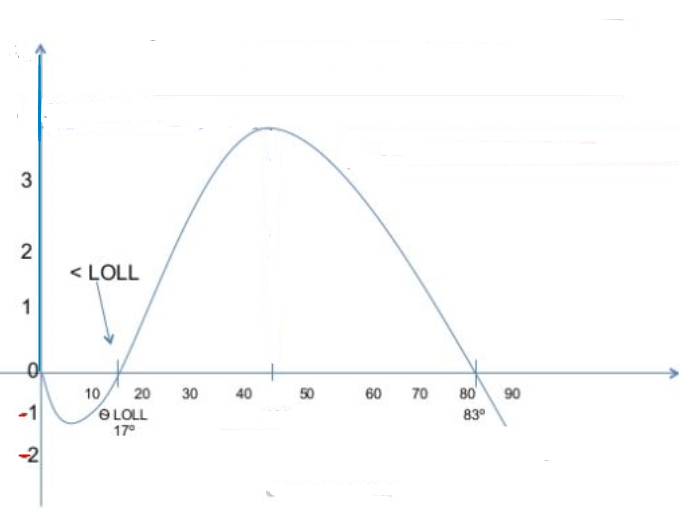
Figur 0240. Angle of loll
Loll, (Engelsk å betyr å sovne av i en avslappendestilling, der man lener seg mot noe). Angle of loll oppstår når GM er negativ, skipet vil krenge over til enten babord eller styrbord til den finner sin hvilestilling (vinkel). Grunnen til at skipet oppnår en hvilevinkel er at bredden i vannlinjeplanet blir større med økning av $\varphi$. Økning i bredden i vannlinjeplanet gir økning i BM slik at formstabiliteten kompenserer for vektstabiliteten. I figur 0240 er hvilvinkel 17 °, utstrekningen er 17 ° - 83 ° (66 °).
I figur 0240 er hvilvinkel 17 °, utstrekningen er 17 ° - 83 ° (66 °).
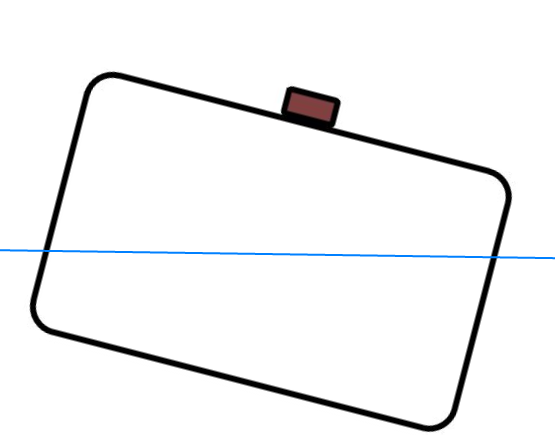
Figur 0241 skip med krengning
Hvis man tenker seg til at man ankommer skipet, i figur 0241 som har krengning til styrbord, uten å kjenne til tilstanden for stabiliteten om bord. Det er ønskelig å rette opp skip slik at det blir null list med å flytte den vekten på dekk ut til babord side. Ser på hva som skjer i to forskjellige tilfeller: 1. Hvis skipet har positiv GM og krengningen skyldes krengende moment til styrbord. Ved å flytte vekten til babord vil skape et krengende moment til babord. Ved å flytte på vekten i rolig hastighet så vil skipet rette seg opp sakte men sikkert. Hvis det krengende moment til babord blir like stort som det til styrbord så vil skipet ligge med null list. 2. Hvis skipet har negativ GM og med en hvilevinkel like stor som visst på GZ kurven lengre opp (17 ° loll til styrbord). Det kritiske med dette tilfelle er at når man flytter vekten over til babord i rolig hastighet så vil skipet falle brått over til babord etter en kort forflytning av vekten. Skipet vil falle helt over til 17° loll til babord, eller rettere sagt noen grader mer alt etter hvor stor bevegelse energi som skapes men vil til slutt falle til ro i hvilevinkel 17° babord. Det vil bli en forandring i list på over 35° og det ville ha føltes ubehagelig for de som er om bord da, med store sjanser for at noen ville ha blitt skadet?

Figur 0242 Bilskip «Coucar Ace»
Bilskipet «Coucar Ace» kantret over under bytte av ballastvann i 2006 i henhold til BWM, litt over 100 NM utenfor Alaska. Skipet var på vei til Vancouver (British Columbia) fra Japan med 4812 personbiler om bord. På den tiden var skipet blant verdens største bilskip med en kapasitet på 5542 personbiler. Skipet mistet stabilitet ved bytte av ballastvann og at det samtidig ble truffet av en stor bølge. Bytte av ballastvann førte til fri væske overflate effekt som igjen medførte til negativ stabilitet. Skipet fikk en angle of loll som var nesten like stor som kantringsvinkel. Den store bølgen skapte et krengende moment slik at Skipet fikk slagside med 60 ° til babord. Skipet ble senere tauet til dypere vann og rettet opp. Lasten med 4812 biler ble ødelagt.
Skip med angle of loll
Et skip med angle of loll i dønninger vil krenge fra den ene siden til den andre for hver dønning.
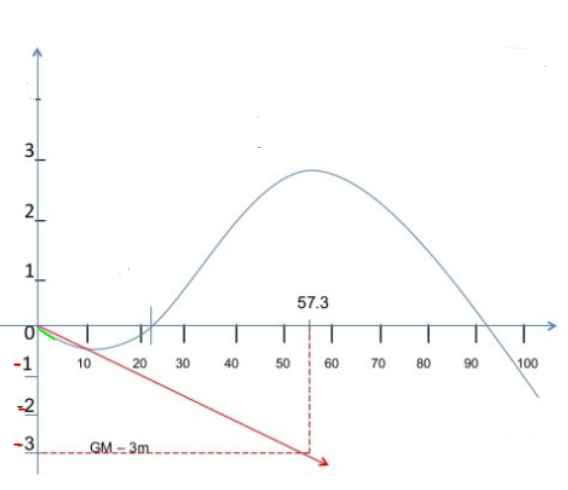
Figur 0243 Angle of Loll med negativt GM
På lik linje som med GZ kurven i figur 0243 så kan man finne GM ved en GZ kurve som har angle of loll og negativ GM. Angle of loll er 22 ° og utstrekning er 22 ° - 92 ° (70 °). GM i dette tilfeller er – 3 meter.
Oppgave til GZ kurver (fra kont- eksamen høst 2018 00TM01K)
Løsning på GZ oppgaven.
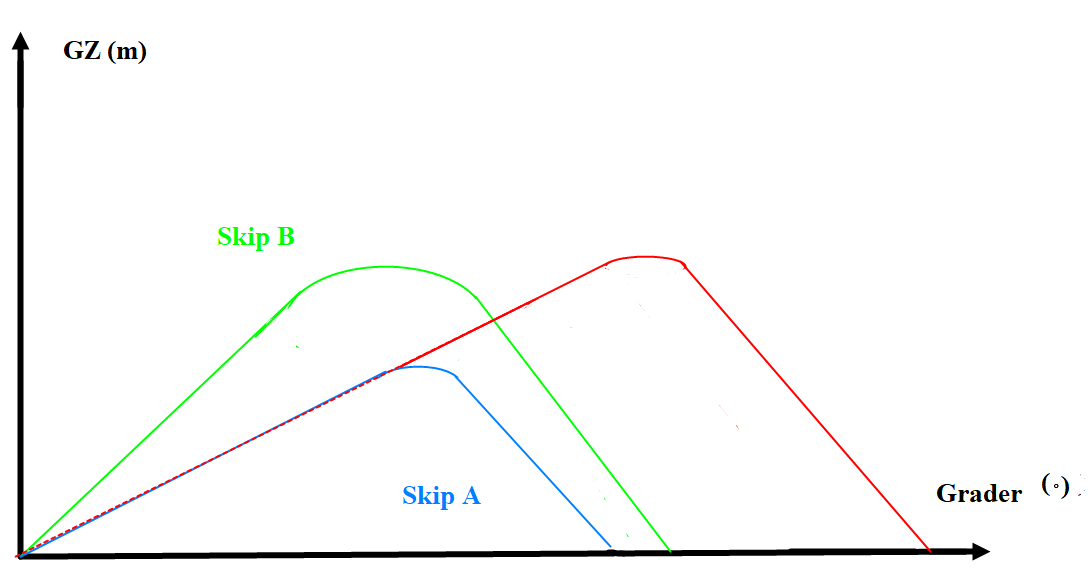
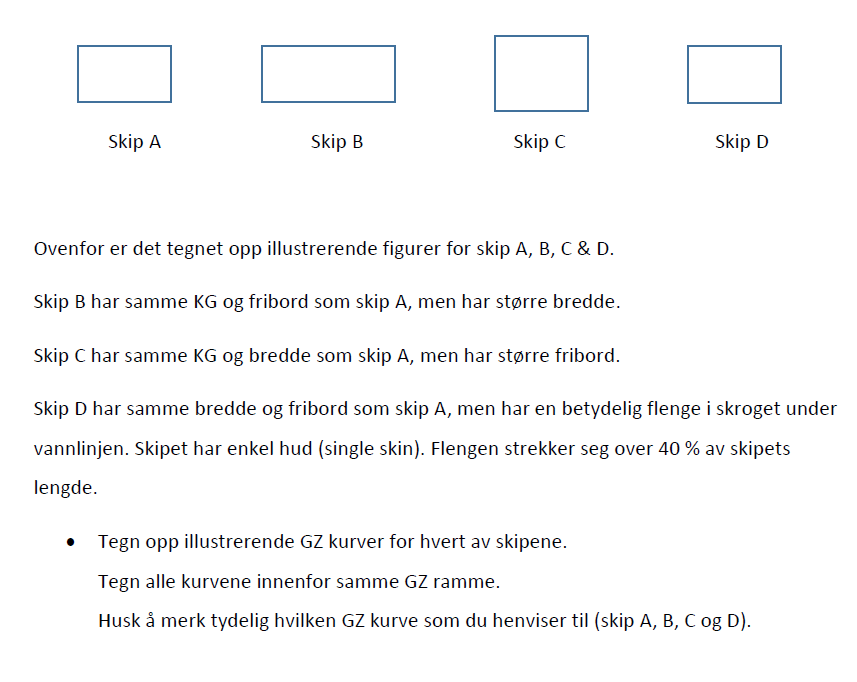
Figur 0244 Forskjellige GZ kurver til GZ oppgaven.
Skip A (blå linje) sin GZ kurve blir et referanse punkt til skip B og C.
Skip B (grønn linje) har samme KG som skip A men har større bredde. Større bredde gir bedre formstabilitet og dermed større GM. Større GM gir brattere stigning på GZ kurven men større bredde gjør at dekkshjørnet kommer i vannet tidligere enn skip A. Skip B får større maks GZ verdi enn skip A
Skip C har samme KG og bredde som skip A, GZ kurven til skip C vil følge kurven til skip A helt til dekkshjørnet kommer i vannet. Større fribord gjør at dekkshjørnet kommer senere i vannet enn skip A. Det medfører at skip C vil få en større krengevinkel før dekkshjørnet går i vannet (reststabilitet). Skip C vil dermed få en større utstrekning på GZ kurven og større maks GZ verdi enn skip A.
Skip D vil (mest sannsynlig) ikke ha noen GZ kurve på grunn av defekt volumdeplasement, etter en så stor betydelig flenge. Skip D vil sannsynlig kantre øyeblikkelig slik som «Rocknes» gjorde.
Statisk og dynamisk stabilitet. Begynnelse stabilitet (initial) betegnes som statisk stabilitet, statisk betyr å være i ro, og være i likevekt. Ved å betrakte et skip med null krengning og ved en krengning på F.eks. 10 grader, så betraktes kun disse to tilstander isolert hver for seg og ikke i en sammenheng. Betraktning av en likevekt mellom det krengende moment og det rettende moment, når metasentre står fast i samme punkt så lar krengnings vinkel $\varphi$ statisk seg lett beregnes , den kan også beregnes grafisk ved å tegne en GZ kurve og en krengende arm kurve , der de skjærer hverandre i første punkt vil være $\varphi$ statisk . Når $\varphi$ statisk er større enn 10 -- 12 ° så må den beregnes kun grafisk. Dynamisk betyr å være i bevegelse, skipet får tilført en bevegelsesenergi av vind, bølger, som medfører en rullebevegelse. Vi skiller de to vinklene: $\varphi$ statisk = $\varphi$s og $\varphi$ dynamisk = $\varphi$d
Beregning av $\varphi$ statisk med både beregning og grafisk for skipet «Linda»:
M/S Linda er i en havn hvor den skal laste både bulk og dekkslast.
Det blir lastet om bord et lokomotiv ved hjelp av en landkran, den skal plasseres midt på lasteroms luke # 5 men landkranen får problemer under hivet, medfører at lokomotivet bli låret ned helt ute i bordet (rekka) ved lasteromsluke # 5.
Hvor stor blir krengningen (i antall grader)? Man antar at lokomotivet belaster dekket med hele sin tyngde.
Opplysning om lokomotivet: Vekt = 175 Tonnes, bredde = 3,13 m, Høyde = 4,58 m. Tyngdepunktet beregnes midt i og 1,5 m opp (fra skinne).
Linda hadde ∆ = 17500 Tonnes og KG = 7,48 m og TCG = 0, før lokomotivet ble plassert på dekk.
Løsningsforslag:
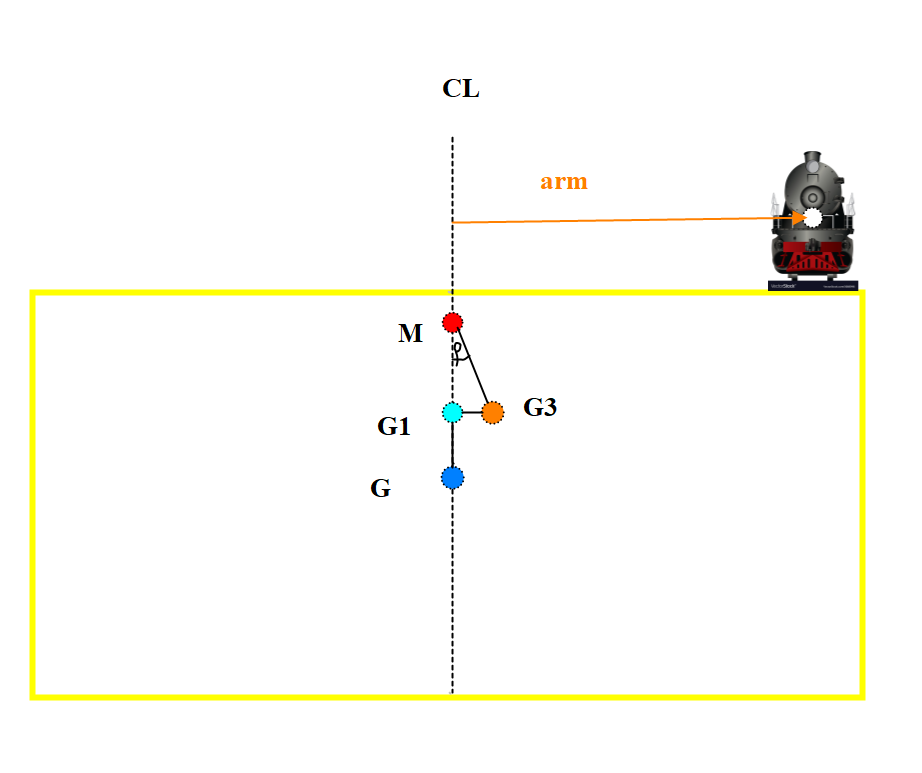
Her blir det økning i ∆, vertikalt moment og krengende moment.
Beregner armene til lokomotivet:
Vertikalt: Dybde i riss + høyde fra dekk til tyngdepunkt til lokomotivet
12,5 m + 1,5 m = 14,0 m
Krengende arm (tcg):
tcg: fra CL til tyngdepunktet til lokomotivet
B/2 – ½ bredde av lokomotivet: 10,2 m - 3,13 m/2 = 8,63 m
| Plassering | Vekt (Tonnes) | Arm (m) fra K | Moment (TM) | Arm fra CL | KRM (TM) |
|---|---|---|---|---|---|
| ∆ | 17500 | 7,48 | 130900,00 | 0 | 0 |
| Lokomotiv | 175 | 14,0 | 2450,00 | 8,63 | 1511,12 |
| Sum | 17675 | sum | 133350,00 | sum | 1511,12 |
KG1 = Sum momenter/∆ = 133350,00 TM/ 17675 Tonnes = 7,54 m
G1M = KM – KG1 = 8,51 m – 7,54 m = 0,97 m
G1G3 (TCG) = KRM/ ∆ = 1511,12 TM / 17675 Tonnes = 0,088 m
Tan $\varphi$ = G1G3/G1M = 0, 088 m / 0, 97 m = 0, 09072 → Arctan = 5, 18°
Grafisk løsning:
Utsnitt av GZ kurven. Her er den grønne linjen den krengende arm, beregnes ved hjelp av cosinus til $\varphi$ : G1G3 × Cos $\text{φ }$. Den er så lite avtagende at man trenger bare å benytte Cos når $\varphi$ er større enn 10° og for hver tiende grad. Deretter plotter disse inn på skjemaet og der hvor den skjærer GZ kurven vil være $\text{φs}$, fordi der er den rettende arm og den krengende arm er like store (likevekt).
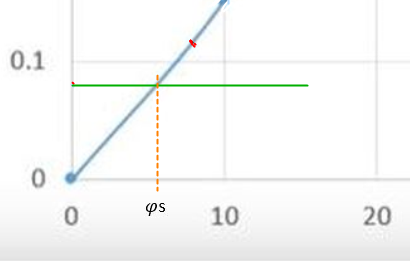
Figur 0245 Grafisk beregning av $\text{φs}$ (statisk)
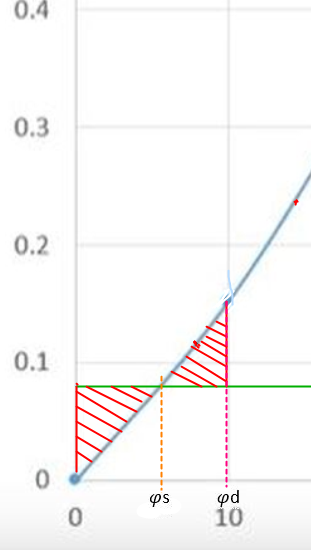
Figur 0246 Grafisk beregning av $\varphi$d (dynamisk)
Betraktning til figur 0246 Hvis lokomotivet på Linda blir låret ned på dekk veldig forsiktig og at man bruker lang nok tid på denne operasjonen så vil skipet krenge til $\text{φs}$ og ikke mer . Hvis lokomotivet blir låret ned rasket mulig eller at det nærmest faller fritt den siste meteren ned til dekk så vil figur bli gjeldende. Her ser man at den krengende arm er større enn den rettende arm helt til $\text{φs}$, og det røde skraverte feltet mellom den krengende arm og GZ kurven er tilført energi i fra det krengende moment. Det er bevegelse energi som blir tilført og som gjør at skipet krenger til en større $\text{φ }$ e$\text{nn φs}$.
Bevegelse energien blir «fanget opp» av det område av GZ kurven som er ovenfor den krengende arm (men under kurven). Her blir bevegelse energien omgjort til potensiell energi og ved et punkt vil skipet ligge i ro for et kort øyeblikk. Dette punktet vil bli $\varphi$d og det kan beregnes ved hjelp av arealbetraktning. Når Arealet av bevegelse energien og den potensielle energien er like stor så vil $\varphi$d være i høyrekant av den potensielle energien. Etter at skipet har vært i ro et kort øyeblikk vil det falle til babord og til $\varphi$ mindre enn $\text{φs}$ og vil vippe (rotere) om $\text{φs}$ flere ganger til begge sider men vil til slutt falle til ro i $\text{φs}$. Arealet av bevegelse energien er under den krengende arm men over GZ kurven til $\text{φs}$ , arealet av potensiell energien er over den krengende arm men under GZ kurven fra $\text{φs}$. Det som kommer under den krengende arm innenfor GZ kurven er tapt stabilitet.
Den krengende arm beregnes for hver tiende grad og ved 60 ° er den halvert i størrelse fordi Cosinus til 60 ° er 0,5. Maks $\text{φd}$ i GZ kurven (figur ) er 78 ° , hvis krengningen blir større er skipet fortapt fordi krengende arm blir større enn rettende arm . Denne vinkelen betegnes også som kantringsvinkel. Dynamisk stabilitet defineres som den energi som må til for å krenge et skip fra 0 ° til en bestemt $\varphi$. Jo større areal en GZ kurve har dess vanskeligere er det å få krenget skipet. Arealet under GZ-kurven representerer størrelsen av dette potensielle arbeid.
Figur 0247 GZ kurve med kantrings vinkel
En nærmere titt på Krengende moment / krengende arm / forskyvning av last
Et skip vil få krengende moment av vind og sjø (bølger), men vil rette seg opp med moment rettende, hvis skipets G er i senterlinjen. Hva skjer med stabiliteten hvis en del av lasten forskyver seg ut til en av sidene?
Figur 0248 forskyvning av last.
Moment: Betingelsene for et moment er at kraften virker 90° på kraften. På figur 0248 ser man at rettende moment innfrir disse betingelser.
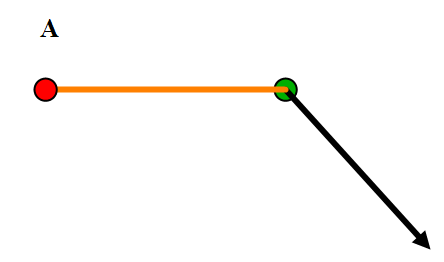
Figur 0249 Kraft som ikke virker i 90 grader.
Hvis man skal beregne momentet om A i figur 0249 så må man kjenne til lengden av arm(oransje) og størrelsen på kraften (sort). I tillegg så må man kjenne til retning Kraften virker i, her ser man at den ikke virker i 90°.
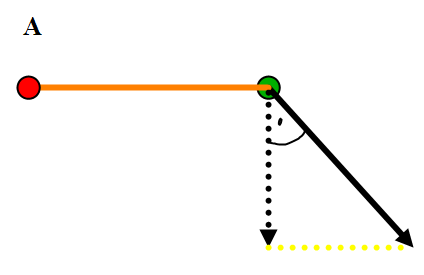
Figur 0250 Dekomponering av krefter
Den stiplete kraften er 90° på armen og vinkelen mellom begge kreftene måles til 40°. En gul hjelpelinje tegnes og den stiplete kraften kan beregnes ved hjelp av trigonometri. Cosinus til vinkel er den stiplete kraft dividert på den heltrukken kraft. Den stiplete kraft vil bli = heltrukken kraft × Cosinus til vinkel. Vinkelen måles til 40°, arm er 2,0 meter og kraft er 20 KN. Momentet om A = 20 KN × Cos 40° × 2,0 m = 30,64 KN.
Samme fremgangsmåte vil bli med skipet G., den må korrigeres slik : GG3* = GG3 × Cos $\varphi$. Her ser man at opprinnelig GZ arm er forkortet tilsvarende den røde linjen. Korrigert GZ arm vil bli: GZ -- GG3*, samme fremgangsmåte benyttes på Kanadisk kornskjema i tabell IX. Tabell IX skal anslå rest(gjenstående) areal av GZ kurven mellom den krengende arm kurven og den rettende arm kurven.
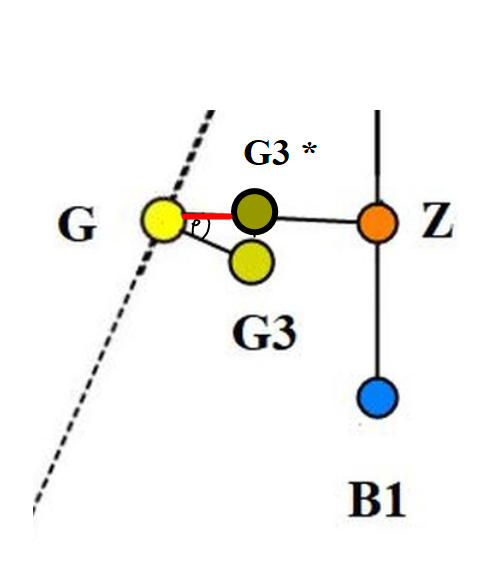
Figur 0251 Korrigert GZ arm
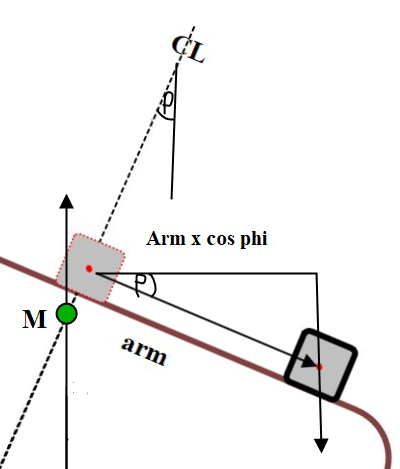
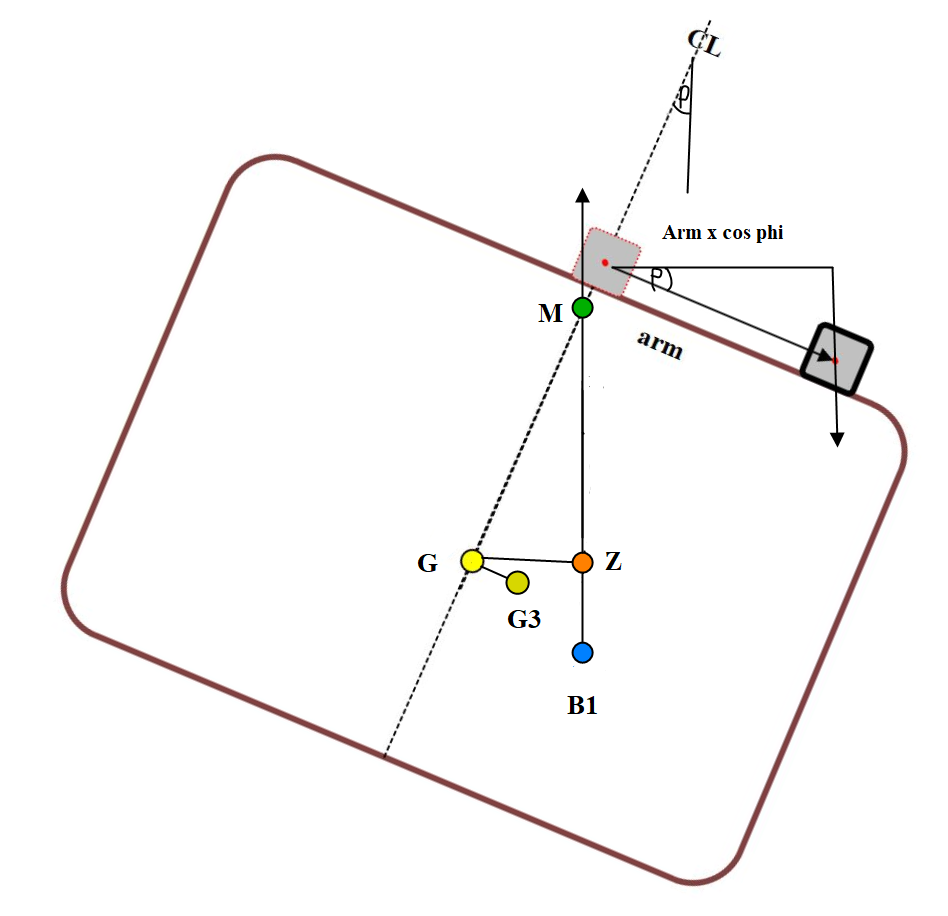
Figur 0252 Krengende arm beregnes : arm x cos $\varphi$.
KRM = ∆ × GG3 × Cos $\varphi$ , KRM = Vekt × arm × Cos $\varphi$. GG3= TCG = Vekt × arm × Cos $\varphi$/ ∆.
Oppgave 7. (Kont eksamen høst 2018 00TM01K)
En kompis kommer på besøk til deg, han har kommet over et dokument til assuranse selskapet VARD, men hendelsesforløpet er ikke fullstendig gjengitt fordi det skifter til uleselig skrift på slutten. Han er nysgjerrig på hva dette dreier seg om?
Han spør om ikke du kan foreta beregninger, komme til en konklusjon og kanskje noen forbedringstiltak? Han tilføyer: Du som er snart ferdig med D1 må jo klare dette?

Konklusjon
…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
Løsningsforslag: Oppgave 7 Kont eksamen høst 2018)
TF 5,55 m
TA 5,45 m Trim = 0,10 m forlig
T¤ 5,50 m → LCF = - 1,55 m. (Hentet fra plansjen)
Beregner x (trim koeffisient) = LCF × trim / LPPX = 1,55 m × 0,10 m / 70,8 m = 0,002 m ≈ 0,00 m
TR 5,50 m → ∆ 3913 Tonnes (b), MTC (b)= 41,53 TM/cm
∆ = ∆ b × 1,020 / 1,025 = 3894 Tonnes,
MTC korrigert = MTC (b) × 1,020 / 1,025 = 41,32 TM/cmBG = Trim × MTC / ∆ = 10 cm × 41,32 TM/cm/ 3894 Tonnes = 0,106 m ≈ 0,11 m
LCG = LCB + BG = 35, 57 m + 0, 11 m = 35, 68 m
FP = lcg 68,97 m. db 3P = lcg 43,63 m, differanse = arm = 25,34 m
Må flytte ballast med vekt = ∆ × GG1 / arm = 3894 Tonnes × 0,11 m / 25,34 m = 16,9 Tonnes = 17 Tonnes.
Arm for KRM (løft) = 6,5 m + 3 m + 2,44 m /2 = 10,72 m
KG = KM – GM = 5,48 m – 0,80 m = 4,68 m
- = benyttet vcg fra plansjehefte for full tank
| Art/plassering | Vekt (Tonnes) | Arm fra K (m) | Moment TM | Arm fra CL | KRM (TM) |
|---|---|---|---|---|---|
| ∆ | 3894 | 4,68 | 18223,92 | ||
| Ballast FP | -17 | 3,84 | -65,28 | ||
| Ballast 3P | 17 | 0,71* | 12,07 | -4,4 | -74,8 |
| FSM FP | FSM | 150,7 | |||
| FSM 3P | FSM | 48,7 | |||
| Løft | 26 | 23 | 598 | 10,72 | 278,7 |
| Sum velt | 3920 | Sum | 19098,67 | Sum | 203,9 |
KG2 = Sum momenter inklusiv FSM / ∆ = 19098,67 TM / 3920 Tonnes
KG2 = 4,87 m
∆ b = ∆ × 1,025/1,020 = 3920 Tonnes × 1,025 /1,020 = 3939 (Tonnes) → T = 5,53 m
KM = 5,487 m
G2M = KM – KG2 = 5,487 m – 4,87 m = 0,617 m ≈ 0,62 m
GG3 = TCG = KRM / ∆ = 203,9 TM / 3920 Tonnes = 0,052015 m
Tan ϕ = G2G3 /G2M = 0,052015 m / 0,62 m = 0,084304 → Arc Tan = 4,81
T1 =B/2 × sin ϕ + T × cos ϕ = 6,5 m × sin 4,81° + 5,53 m × cos 4,81° = 6,05 m
Dybde ved «Delta» =Opprinnelig T 5,50 m + loddskudd = 5,50 m + 0,45 m = 5,95 m
Konklusjon:
#Konklusjon
Skipet tok nedi siden beregnet dypgang ved 4,81° er 6,05 m, mens at dybden kun var 5,95 m ved loddskudd midtskips ved ankomst. Trolig litt bunnskade, innbøyning av plater men har tilstrekkelig med GM til at den ikke kan bli nærheten av negativ (kraft P vil bli så liten), kanskje skadet en av dekksbesetningen seg også med fall ol.? Om bunntouchen førte til at «løftet» røk fremgår ikke, lite trolig men sikkert en ubehagelig opplevelse for de som var involvert. Det ser ut som om at transferen fra FP til 3P kun tok hensyn til at skipet skulle ligge "Even Keel", og at løftet ikke var beregnet med hensyn på begrensningen i dypgående.
Forbedringstiltak:
Mer kontravekt i 3p eller / og at konteiner ble plassert så nært kaikanten som mulig.
For å foreta et sikker løft: fylt mer ballast når løftet starter og lenset ut etter hvert når den svinger inn over dekk (slik at list = tilnærmet lik 0° under mesteparten av løftet). Slik som det ble foretatt med list 4,8°, er en betydelig list, de fleste vanlige kraner har begrensinger med list over 5°.
(anmerking: Hensikten med denne oppgaven var å ta problemstillingen opp på et høyrere nivå(ledelsesnivå), der det ikke stiltes spørsmål slik som: Hva ble GM, Hva ble krengningen og hva ble dypgangen (T1) under løftet OSV. Her skulle kandidatene få resonere og kunne stille alle relevante spørsmål selv)
Tungløft og når løftet ryker.
Når et skip løfter last (vekt) med egen kran så vil det få innvirkning på tverrskipstabiliteten. Skipets tyngdepunkt vil få en vertikalt heving fordi vekten som blir løftet opptrer som den virker i «Bomnokken» til skipets kran. Når løftet blir svingt på utsiden av rekken så vil det krengende moment bli større enn om vekten var plassert om bord. Virkningen av begge disse to vil bidra med at krengevinkel blir større. Det krengende moment GG3 × Cos$\text{ φ}$ virker uavhengig av høyden og med mindre GM på grunn av vertikalt heving av skipets G så vil det krengende moment få mer innvirkning , slik at krengevinkel $\varphi\ $ bli større. Ved tungløft (vekt over 20 Tonnes) så er det anbefalt en GM på 1,0 meter eller mer.
Figur 0253. Et skip sett akten ifra , med krengning til styrbord.
Når løftet ryker: Ser på to forskjellige tilfeller. 1. Skipet ligger oppreist (null list) når løftet ryker men har kontravekt (ballast). I dette tilfelle trenger man bare å tegne opp en GZ kurve uten tungløft og en krengende arm til kontravekten. Dette kan tegnes på styrbord side selv om kontravekten er på babord, hvis skipet er symmetrisk om senterlinjen. Beregning grafisk: se på $\varphi$s og i $\varphi\text{d i }$figur0254.
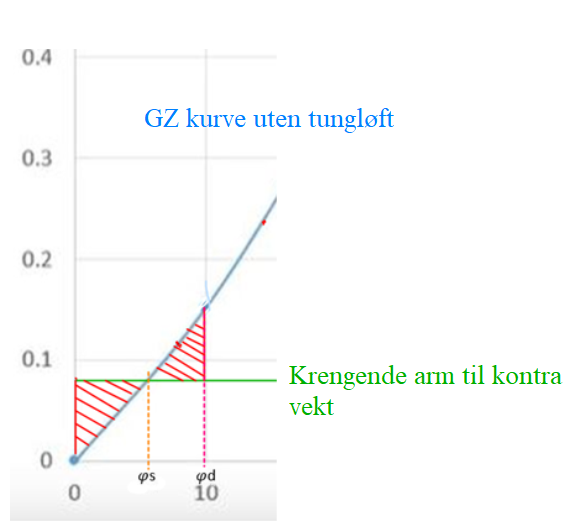
Figur 0254 grafisk beregning av $\text{φd}$
Tilfelle 2. Skipet ligger med styrbord list når løftet ryker.
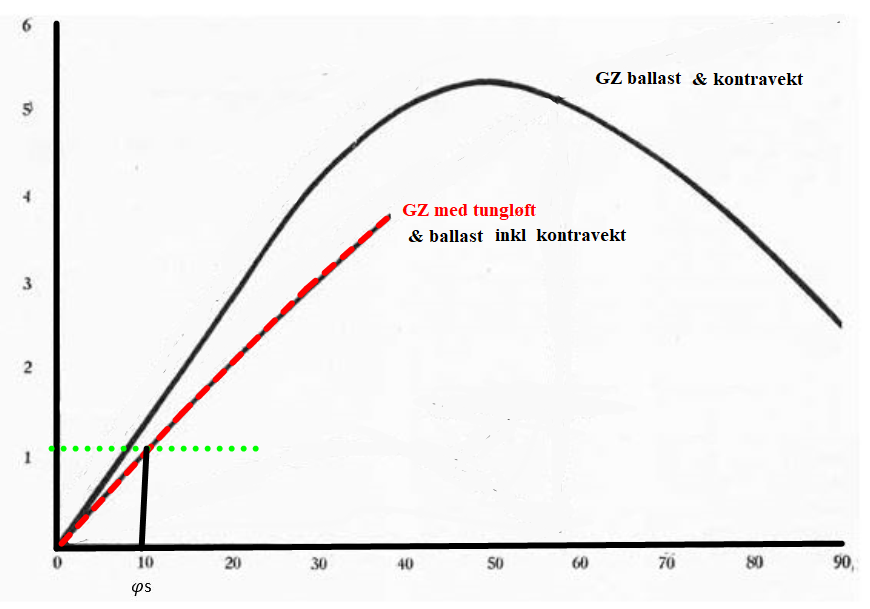
Figur 0255 Grafisk beregning av $\text{φd}$ når skipet ligger med styrbord list når løftet ryker.( første del)
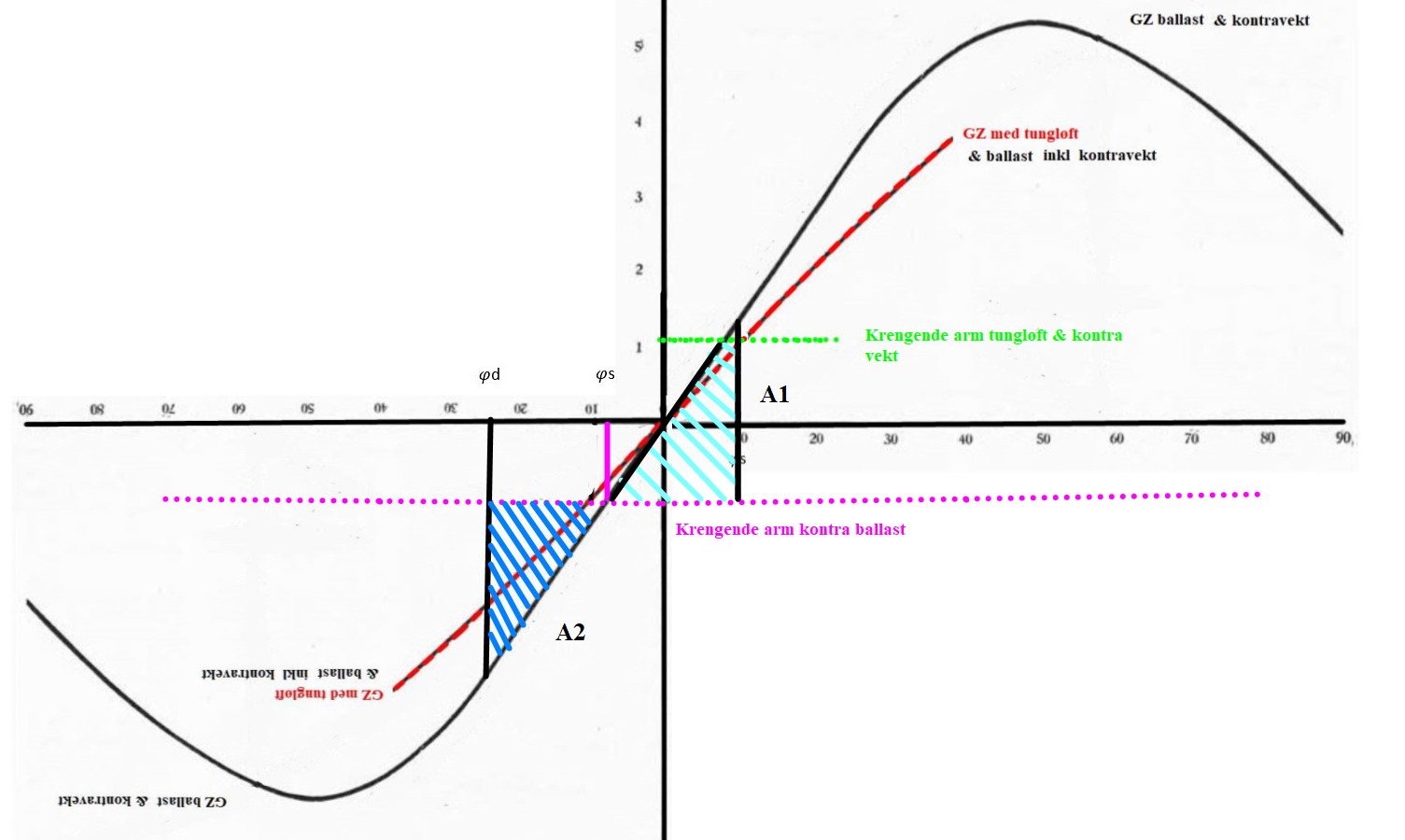
Figur 0256 Grafisk beregning av $\text{φd}$ når skipet ligger med styrbord list når løftet ryker.( siste del)
Lab forsøk på UIT «Når løftet ryker»:
Våren 2017 deltok D1 klassen ved Fagskolen i Troms (avdeling Tromsø) på lab forsøk ved Institutt for teknologi og sikkerhet (UIT). Lab oppgavene bestod i: Krengeprøve, Fri væske overflate effekt og tungløft «Når løftet ryker». Den siste oppgaven ble $\text{ φ}$ dynamisk ($\varphi$d) beregnet grafisk på GZ kurve til 15,6 ° (babord). Forsøket ble målt med en mobiltelefon med klinometer som ble festet til modellen. Filmsnutten (figur 0259) viser hele rulleutslaget der $\varphi$ dynamisk ($\varphi$d) ble målt til 16° men det kan komme av litt fravik eller at klinometret viser 16° når 15,5° er passert?

Figur 0257 kun med kontravekt ( $\text{φs}$ 5 ° Babord)

Figur 0258 med tungløft og kontravekt ($\text{φs }$5° Styrbord)

Figur 0259 Videosnutt av når løftet ryker. ( https://www.youtube.com/watch?v=ywhHJraomsg )
En nærmere titt på stabilitet på fiskefartøy:

Figur 0260 Fiskebåt under 21,0 meter
I den senere tid har det forekommet flere fiskebåter med uvanlige konstruksjoner, de har fått betegnelsen «paragrafbåter». Det gjelder spesielt for fiskebåter med lengde under 21,0 meter, 15,0 meter og 10,67 meter, der disse lengdene angir kvotegrunnlaget. Båtene er bygget med større bredde og høyere skrog /overbygning enn normalt og derav betegnelsen «Paragrafbåt». Hvis man skal gjøre en generell betraktning om stabiliteten til båten på figur 0260 der stabiliteten er godt innenfor myndighetens krav. Bredden er halvparten av båtens lengde (20,99 meter) og høyde over vannlinjen til shelterdekk er i underkant av 7 meter.
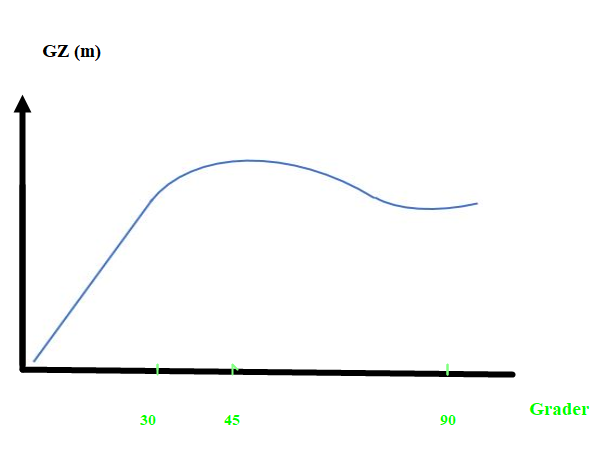
Figur 0261 GZ kurve til fiskebåt i figur 0260.
GZ kurve stigning, stor bredde gir større BM, større BM gir større GM og brattere kurve, større GM gir større GZ. Hvordan kan det ha seg at GZ verdien er så stor ved 90 ° list? Det høye overbygget med shelterdekk gjør at bredden i vannlinjen forblir med stor verdi, selv med 90 ° krengning. Se figur ..for antatt plassering av vannlinje og med antatt effektiv bredde i vannlinjen ved 90° list. Den prikkete linjen angir vannlinjen plassering men uten effektiv bredde.
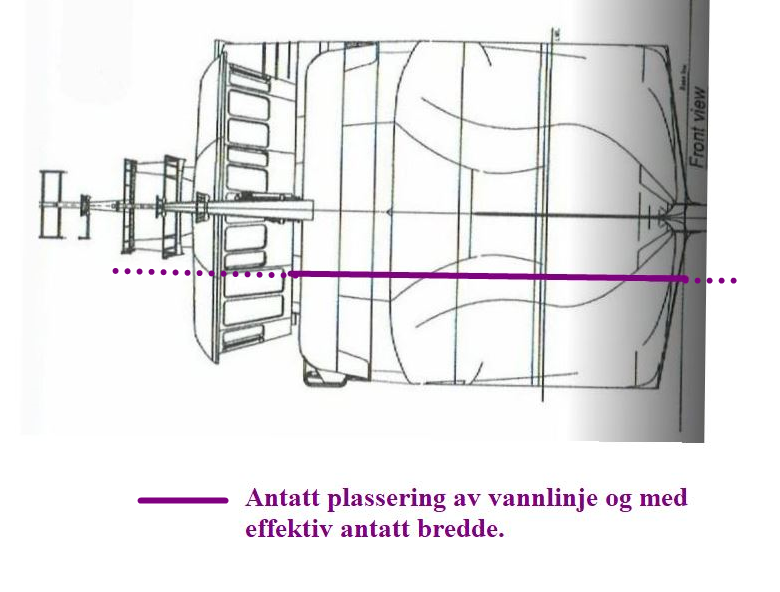
Figur 0262 Fiskebåt med 90 graders krengning
Figur 0262 antatt plassering av vannlinje og med antatt effektiv bredde i vannlinjen ved 90° list.
Hvis man ser nøye etter på figur 0264 så er setterlukene åpne (i hekken) men drageluken er lukket. Hvordan blir GZ kurven når de står åpne? Kanskje den blir sånn som i figur 0263? Med lukene åpne så blir stabiliteten kraftig endret.
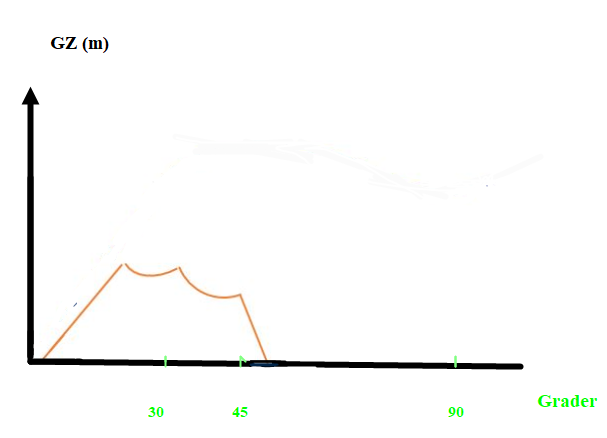
Figur 0263 GZ kurve med settelukene åpne

Figur 0264 settelukene.
Skissen i figur 0260 har betegnelsen SC21 «MAX» og fikk navnet «Fay», tegnet og konstruert av Seacon (Måløy) og bygget av Stadyard på Raudeberg. Det var en kombinert line- og garnbåt, med lengde på 20,99 meter kom den inn under kvotegrunnlaget for fiskefartøy mellom 15 og 21 meter. Fay ble satt i drift november 2018 og i desember 2019 forliste den under setting av line nordøst for Honningsvåg. Værforhold var sterk kulling og 2 – 3 meter bølgehøyde da ulykken inntraff. Et strømbrudd førte til at styringssystemene og hydraulikken om bord sviktet (motorstans på hjelpemotor). Styremaskin fungerte ikke etter strømstansen og båten mistet styringen, ugunstig kursretning gjorde at båten begynte å krenge og det kom sjø inn setteluka. Med svikt i hydraulikksystemet så var det ikke mulig å få stengt settelukene. Hele besetningen ble reddet av redningshelikopters i tide før båten sank. Staten Havarikommisjon avdeling sjøtransport har iverksatt undersøkelse av forliset med type hendelser: Stabilitetssvikt, forsvunnet/savnet fartøy, teknisk svikt, fremdrift eller hjelpemaskineri.
Det foreligger ingen utarbeidet rapport i fra undersøkelsesmyndigheten ennå, men rapporten skal gjøres tilgjengelig innen 12 måneder etter at ulykken inntraff. Dersom dette ikke er mulig, skal undersøkelsesmyndigheten utgi en foreløpig rapport innen 12 måneder.
M/S Fay overlevering fra verftet ble to måneder forsinket på grunn av utfordring rundt stabilitetsberegningene. Det er hevdet at det ble tilført vekter i kjølen i dette tidsrommet. SC21 «MAX» var et nytt konsept og nytt fartøydesign, der lastevolumet var på 190 m3.M/S Fay ble ombygget i løpet av våren 2019 for å øke ballastkapasiteten men det er fortsatt uvisst om denne ombyggingen fikk innvirkning på stabiliteten? Det er allerede tatt til ord innenfor næringen som vil skrote begrensinger på lengde og bredde og heller legge begrensinger på lastevolum. Det er strenge krav til stabiliteten for fiskebåt med denne størrelsen, viser til Forskrift om konstruksjon, utstyr, drift og besiktelser for fiske- og fangstfartøy med største lengde på 15 meter og derover (Lovdata.no). Her kan nevnes: Minstekrav til stabilitet som skal være oppfylt: GM ikke mindre enn 0,35 meter, Arealet under GZ-kurven skal ikke være mindre enn 0,055 meterradianer opp til 30 graders krengningsvinkel og ikke mindre enn 0,090 meterradianer opp til 40 grader eller fyllingsvinkelen$\text{ φ}$f dersom denne vinkelen er mindre enn 40 grader. I tillegg skal arealet under kurven mellom krengningsvinklene på 30 grader og 40 grader eller mellom 30 grader og $\varphi$f hvis denne vinkelen er mindre enn 40 grader, ikke være mindre enn 0,030 meterradianer. Den rettende arm skal være minst 200 millimeter ved en krengningsvinkel som er lik eller større enn 30 grader. Største rettende arm GZmax skal inntreffe ved en krengningsvinkel som fortrinnsvis er større enn 30 grader men som ikke er mindre enn 25 grader. Fartøyets metasenterhøyde (GM) i lett tilstand skal være positiv. For fartøy med lengde (L) under 24 meter, skal i tillegg den rettende arm for krengevinkler mellom 40 og 65 grader ikke noe sted være mindre enn 100 millimeter, og positiv opp til 80 grader (utstrekning), når det ses bort fra fylling gjennom luker, dører, lenseventiler e.l. som må stå åpne under drift, men som raskt kan lukkes værtett. Værtette dører:) Alle adkomståpninger i skott til lukkede overbygninger og andre ytre oppbygninger som vann kan trenge inn gjennom og derved sette fartøyet i fare, skal være utstyrt med dører permanent festet til skottet. Dørene skal kunne lukkes værtett og være innrammet og avstivet slik at hele konstruksjonen er av tilsvarende styrke som skottet for øvrig. Innretningene til å sikre at disse dørene er værtette skal bestå av pakninger og tilsettingsanordninger eller andre likeverdige midler og skal være permanent festet til skottet eller dørene. Dørene skal være anordnet slik at de kan betjenes fra begge sider av skottet. Vanntette dører: Antall åpninger i vanntette skott som fastsatt i § 2-1 tredje ledd skal reduseres til det minimum som er forenlig med fartøyets arrangement og driftsmessige behov.
Åpninger skal være utstyrt med vanntette lukningsmidler i henhold til § 2-1 første ledd. Vanntette dører skal ha tilsvarende styrke som skottet de er anbrakt i. (2) På fartøy med
lengde (L) under 45 meter kan slike dører være av hengslet type. Dørene skal kunne betjenes lokalt fra begge sider og normalt holdes lukket i sjøen. Et oppslag om at døren skal holdes lukket i sjøen, skal festes på begge sider av døren. Vanntette skyvedører skal kunne betjenes når fartøyet krenger inntil 15 grader til hver side. Vanntette skyvedører skal, enten de betjenes manuelt eller på annen måte, kunne betjenes lokalt fra hver side av døren. For fartøy med lengde (L) på 45 meter og derover skal disse dørene også kunne betjenes ved fjernstyring fra et tilgjengelig sted over arbeidsdekket, unntatt når dørene er anbrakt i innredningen for besetningen. Vanntett integritet: Utvendige åpninger skal kunne lukkes værtett for å forhindre at vann trenger inn i fartøyet. 1 Luker i dekk som kan være åpne under fiske, skal normalt være arrangert nær fartøyets senterlinje. I større lukedeksler, over 4 m², skal det til bruk under drift være anbrakt små lukedeksler nærmest mulig fartøyets senterlinje. Større lukedeksler skal ha tilsettinger også på eventuell hengselside. Hengslede lukedeksler skal kunne sikres i åpen stilling. Sjøfartsdirektoratet kan godkjenne andre arrangementer dersom sikkerheten ikke reduseres.) Fiskeluker på hekktrålere skal være kraftoperert og kunne betjenes fra et sted der det er fritt utsyn til lukene.
I tillegg skal det utarbeides sju forskjellige lastetilstander (driftstilstander), eget krav til ising, krengeprøve.
Ringnotsnurper: Ringnot er et fiskeredskap som brukes for å fange stimfisk. Den består av ei stor not som settes rundt stimen og snurpes sammen i bunnen. I norske farvann brukes ringnot for å fiske sild, brisling, makrell, lodde, sei og kolmule. Den eldste typen er snurpenot og ble brukt fra fartøyer kalt snurpere fram til midten av 60 tallet. Nota ble dratt sammen fra småbåter (doryer) og fortøyd langs sida av snurperen. Fangsten ble tatt om bord i snurperen ved hjelp av en håv. På midten av 1960-tallet overtok ringnotsnurperne. De setter og tar sammen nota fra hekken av båten med kraftblokk eller not vinsjer, kraftblokken gjorde sitt inntog i 1957. Nota har blylodd og flytelegemer av plast så den skal flyte riktig. Snurpelina er en stålvaier. I begynnelsen brukte de håv men etter hvert ble fisken pumpet ombord ved hjelp av ei fiskepumpe. Ringnot og kraftblokk ble introdusert i fiskeflåten på midten av sekstitallet som en videreutvikling av den eldre snurperen med doryer.

Figur 0265 M/S Hugo Trygvason
Hugo Trygvason ble ombygget til ringnotsnurper i 1965 BRT 593, opprinnelig en hvalbåt, fisket sild og lodde. Figur 0265 viser Hugo Trygvason inn fra feltet for å losse fangst, som bildet viser er det lite fribord og vann på dekk. Ved lasting av fangst på feltet, håv første år og senere pumpe, så ble det tilført vann i lasterommet men dette ble lenset ut med en pumpe i løpet av kort tid. Det første året brukte den posebåt og håv, på den første turen hadde den trebinger på dekk for fangst men det medførte at den ble for «tung» og disse ble fjernet. På den andre turen i Austhavet på vei til Honningsvåg for å losse, ble snurperen overasket med Nordøstlig storm rett nord om Berlevåg. Det kom sjøvann på oljetankene og motoren stoppet, snurperen drev på tvers i stormen og det ble besluttet og låre den ene posebåten. De fleste av mannskapet gikk om bord i båten mens noen få tok seg frem på bakken med livet som innsats, holdt på å bli skylt over bord, for å la gå det ene ankeret. Etter en stund fikk ankeret feste i bunnen og baugen rettet seg opp mot været og til slutt fikk de start på motoren. Hugo Trygvason fikk assistanse av en redningsskøyte og et kystvaktskip. Det viste seg i ettertid at det var kommet 60 Tonnes med sjøvann på oljetankene.

Figur 0266 .M/S Grimsholm.
Figur 0266 viser M/S Grimsholm i Nordsjøen (1964) etter å ha fått et kast med 4000 hl makrell i nota. Dette var lenge det største kastet som var tatt opp. I følge skipperen så var det en ny og overdimensjonert not og i tillegg stod det folk klar med øks for å hogge av nota i kraftblokka. Det store krengende moment skyldes at nota i kraftblokka har stor mengde, samt at det hives inn med håv. Bomnokken til håven har også høyt tyngdepunkt. Et annet faremoment er at makrell ikke har svømmeblære og den må holde seg i bevegelse hele tiden for unngå å synke Hvis nota strammes for mye inn, dras for tett sammen, synker makrellen og den vil medføre en kjempetyngde. Det er flere båter som har kantret og blitt dratt nedover i havet på grunn av dette slik som med M/S Kjellungen i 1972.
Figur 0267 Illustrerende GZ med krengende arm for ringnotsnurper med not i kraftblokken og som håver inn fangst.
Ved å betrakte de to ringnotsnurpene ovenfor så ser man: Lite fribord, vann på dekk, vann i lasterommet (FSM midlertid), vekt av not i kraftblokken, våt og tung not som hales inn oppe på galgedekk, vekt av håv med høyt tyngdepunkt, og i tillegg bølger og vind. Resultatet blir en begrenset GZ kurve og et relativt stort krengende moment som medførte at det var en del ringnotsnurpere som kantret over og gikk fortapt på 50 og 60 tallet.
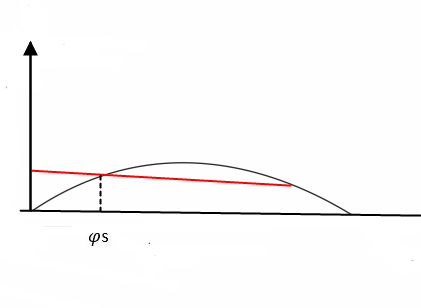
Statisk stabilt: Fra figur 0267 er $\text{φs}$ ( $\text{φ statisk }$) tegnet inn. Her er rettende arm og krengende arm like stor (likevekt). Skipet er da statisk stabilt. Hva blir statisk ustabilt? Figur 0268 viser eksempel på statisk ustabilt.
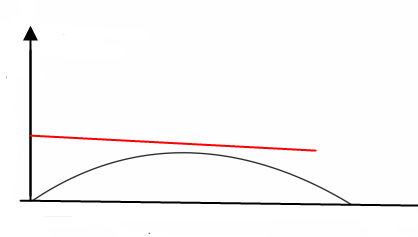
Figur 0268 Statisk ustabilt
Dynamisk stabilt og dynamisk ustabilt:
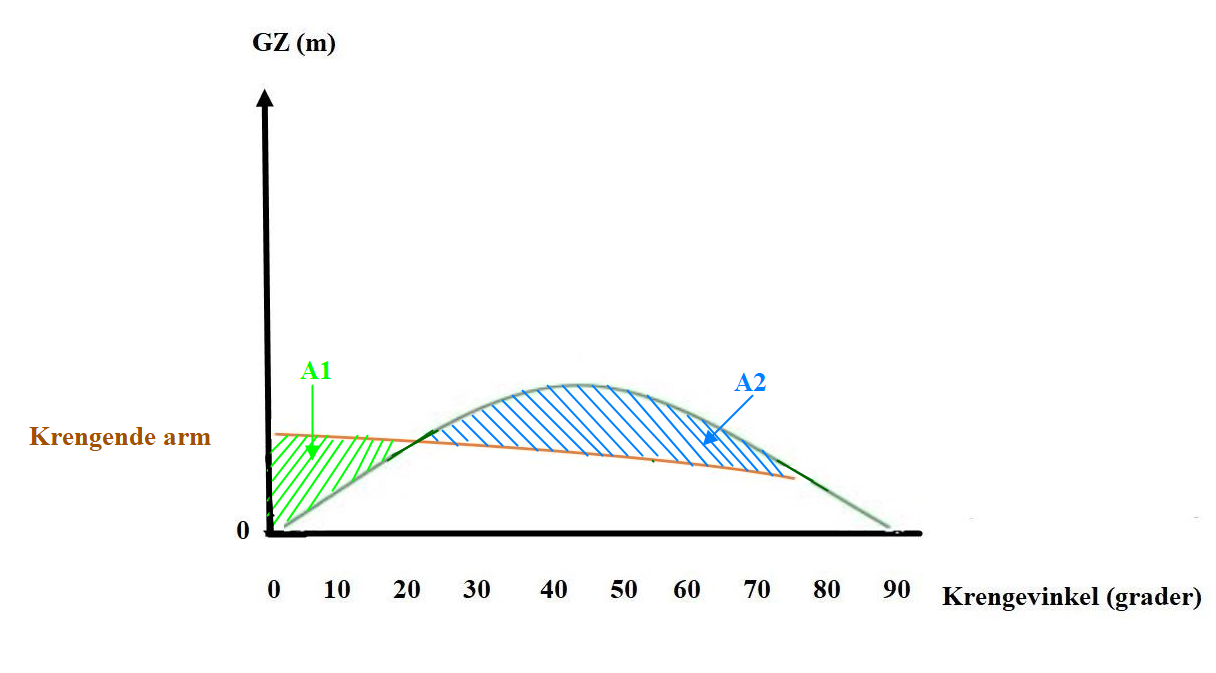
Figur 0269 Viser statisk stabilt og dynamisk stabilt
Figur 0270 Viser statisk stabilt og dynamisk ustabilt.
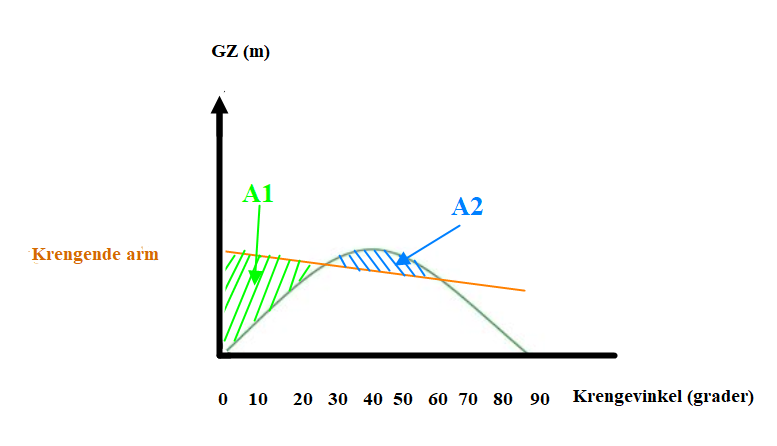
Ulykkene med ringnotsnurpere og snurpere på 50 og 60 tallet som nevnt ovenfor skyldes som oftest at de var statisk stabil men dynamisk ustabil. Fra figur 0269 og figur 0270 ser man lett om det er dynamisk stabil eller ustabil, hvis arealene (A1 og A2) er omtrent like store så må de beregnes med hjelp av Simpson formel for å bestemme hvem som er størst

Figur 0271 viser cruiseskip Anthem of the Seas
Moderne Cruiseskip og sjødyktighet:
Det er fra flere hold hevdet at store og moderne cruiseskip ikke er sjødyktige, er topptung og ustabil. I februar 2016 var cruiseskipet «Anthem of the Seas» på vei fra New York til Port Canaveral (Florida) da den kom ut i en forrykkende orkan. Det ble rapportert vindkast på 150 – 160 knop og bølgehøyde på 10 meter fra søndags ettermiddag til mandagsmorgen. Skipet returnerte tilbake til New York, det var kun fire passasjerer som fikk lettere skader. Det var 4529 passasjerer og 1616 mannskap om bord, bølger slo inn på femte promenadedekk og slo av deler av et glassfiberskott som landet i svømmebassenget. Skipet har Brutto tonnasje: 168,666, lengde: 347,06 meter, Bredde: 49,4 meter(maks) og 41,4 meter i vannlinjeplanet og dypgående er 8,80 meter. Et skip kan ikke bedømmes kun etter sitt utseende men Stabilitet avhenger av mange faktorer - skipets vertikale tyngdepunkt, treghetsmomentet til vannlinjeplanet, areal under rettende arm kurve (GZ), vindstyrke, fri væskeoverflate effekt og så videre. Skipet har stor bredde i vannlinjeplanet og dette gir meget god formstabilitet, samt at det er brukt lette konstruksjons elementer i øvre del av overbygning.
GZ kurve med korn (last) som har kastet
Etter den 2. verdenskrig så var det et stort behov for transport av matprodukter, spesielt til Japan som ikke har jordbruksland, her ble det fraktet store mengder med korn på bulkskip. Kornet har en glatt overflate og har en rasvinkel (hvilevinkel) på om lag 30 grader. Det medførte at det var mange ulykker med bulkskip på 40, 50 og 60 tallet. Figur 0272 illustrerer tilstanden til et lasterom hvor kornet har kastet, tyngdepunktet til lasterommet er skjøvet ut til siden og samtidig flytte seg vertikalt oppover. I SOLAS 1948 kom det krav til kornlasting, ved dannelsen av IMO så kom det regler for kornlasting i 1960 og 1969, men det var i SOLAS 1974 at det ble innført å beregne krengende moment ved kornkasting med sikkerhetsmargin på 6 % på fylte rom og 12 % for delvis fylte rom. Senere kom en egen kode for lasting av korn i 1991 (International grain code). Kapittel VI i SOLAS omhandlet lenge bare om kornlasting.

Figur 0272 viser et delvis fylt lasterom med korn på et bulkskip som har kastet.
Et skip som foretar eksempelvis et tungløft vil få et krengende moment i noen minutter men et bulkskip med lasterom der kornet har kastet vil få krengende moment som vedvarer helt til lossehavnen. Et bulkskip som laster korn må ha null list etter at lastingen er komplett , $\varphi$ statisk ved kasting kan maksimum være 12 grader. Det er krav til areal (gjenstående) på GZ kurven etter at kornet har kastet og det er 0,075 meterradianer.
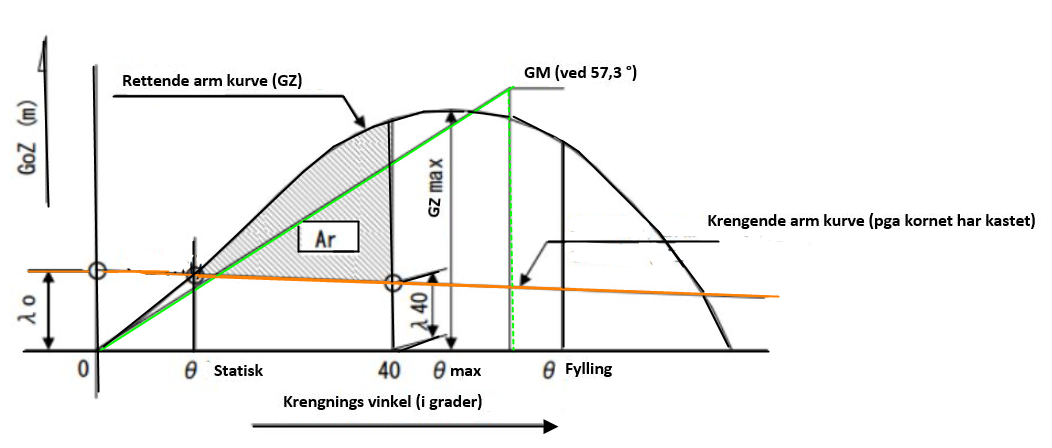
Figur 0273 GZ kurve ved kornlasting
Figur 0273 viser GZ kurve ved kornlasting, Ar = Area Residual som betyr gjenstående areal. Alt som kommer under den krengende arm kurven er fortapt stabilitet og det er derfor det er krav til Area Residual. Hvordan gjør man det? Det gjøres på et kornskjema (Kanadisk), først beregnes og tegnes en aktuell GZ kurve, så beregnes krengende arm for null grader og for førti grader (λ 0 og λ.40) og disse settes ut som to punkter på GZ kurven. Det tegnes en linje mellom disse to punktene, som er den oransje linjen på figur. Ved for eksempel på 15 grader måles den rettende arm og verdien av den setter man inn på 1st korrekted GZ verdi i 15 grader rubrikken. Det samme gjør man med den krengende arm for samme vinkel og den setter man inn i upsetting arm rubrikken. Den helt korrekte GZ verdi beregnes slik = Rettende arm (15 grader) - krengende arm (15 grader).
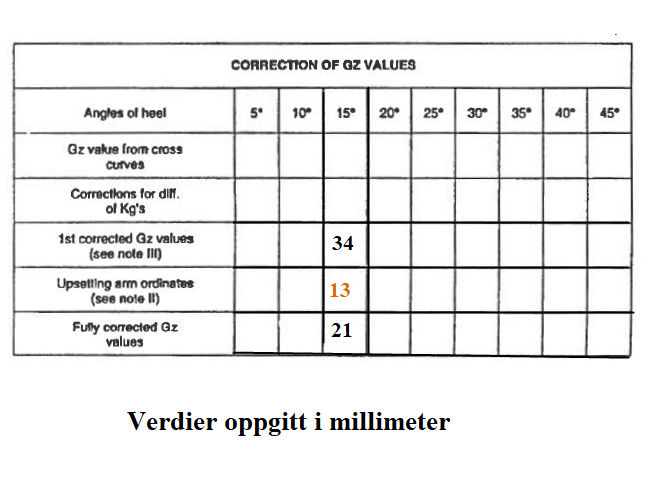
Figur 0274 Tabell i fra kornskjema der man beregner den gjenstående rettende arm
Siden alt av den rettende arm under den krengende arm er fortapt så beregnes det gjenstående arealet mellom $\varphi$ statisk og 40 grader. Krav for å beregne areal etter Simpsom formel er at antall ordinater er oddetall og at avstand (a eller intervall) mellom de er den samme. Hvis det er nødvendig med repetisjon for beregning av areal med Simpsom formel , se K12 Lærebok i lastbehandling kapittel 1 (www.marfag.no). Intervall = (40 grader - $\varphi$ statisk )/ 6 . Det første ordinat er $\varphi$ statisk og det blir seks ordinat til slik at det blir totalt sju ordinat. Hvis $\varphi$ statisk er 5 grader så blir intervall = (40 grader -- 5 grader) / 6 = 5,83 grader. Det andre ordinat blir ved: 5 grader + 5,83 grader = 10,83 grader, det tredje ordinat blir ved: 10,83 grader + 5,83 grader = 16,66 grader. Det sjette ordinat blir ved 34,15 grader og det sjuende blir ved: 34,15 grader + 5,83 grader ≈ 40 grader.
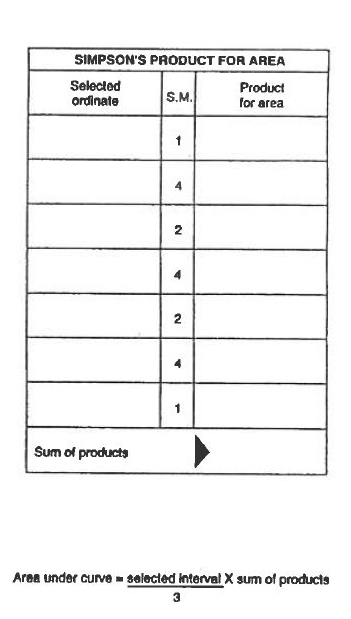
Figur 0275 viser tabell og Simpson faktor for beregning av produkt (kornskjema), den under er formel for Areal.
Fra IMO Internasjonale kode på intakt stabilitet 2008 (SOLAS 1974)
Kodens formål er å presentere obligatoriske og anbefalende stabilitetskriterier og andre tiltak for å sikre sikker drift av skip, for å minimere risikoen for bestemte typer skip, til personellet om bord og til miljøet. Del A av koden adressere de obligatoriske kriteriene og del B inneholder anbefalinger og tilleggs retningslinjer. Fra kapittel 2 (del A): 2.3 Ekstrem vind og rulle kriterium.
Evnen til et skip å motstå de kombinerte virkningene av tverrskips vind og rulling skal være demonstrert som følger:
-
Skipet utsettes for et konstant vindtrykk som virker vinkelrett på skipets senterlinjen som medfører et konstant krengende vind arm lw1 (som er under den røde krengende arm kurven).
-
Fra likevekts vinkelen $\varphi$0 , antas skipet å rulle over til babord på grunn av bølger for så å rulle i mot styrbord til en rullevinkel $\varphi 1$ med vinden. Denne rullevinkel med konstant vind skal ikke overstige 16 grader eller 80 % av vinkelen der dekkshjørnet kommer i vannet.
-
Skipet skal så bli utsatt for en kastevind som medfører krengende vind arm lw2 (under den oransje krengende arm kurven)
-
Under disse omstendigheter skal areal av b være like stor eller større enn areal a (se figur ...). Der $\varphi\ 2$ er fyllings vinkel $\text{φf }$eller 50 grader , (der den som er minst gjelder).
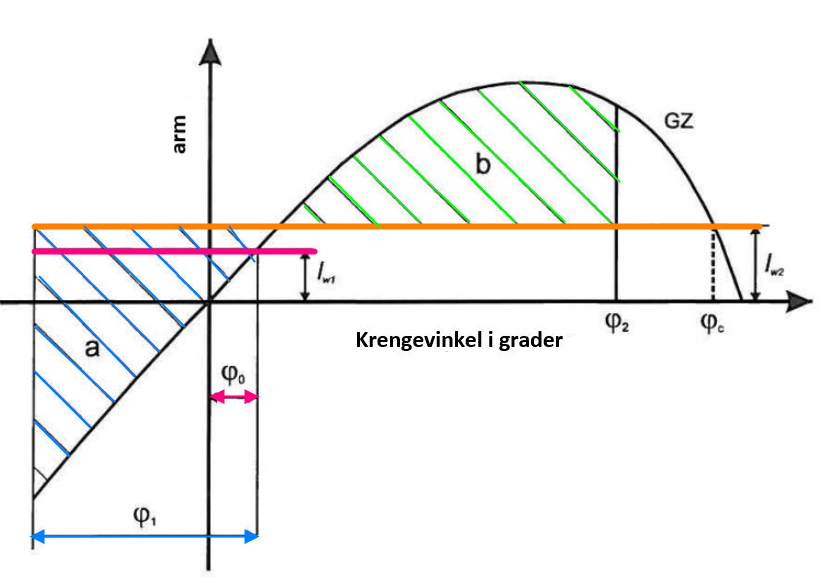
Figur 0276 GZ kurve som har vind og kastevind, samt rullebevegelse (bølger).
Der formel for lw1 = (P × A × Z)/ 1000 × g × ∆, (m)
P = vindstyrke på 50 knop (504 Pascal) (Pa), men denne kan bli redusert av administrasjonen der skipet fører flagg)
A = prosjektert tverrskipsareal av skipet og dekklasten som er over vannlinjen (m2)
Z = Vertikal arm fra senter av A til T/2 (dypgang/2) (m)
∆ = Vektdeplasement (Tonnes)
g = gravitasjons akselerasjon (9,81 m/s2)
Formel for lw2 = 1,5 × lw1, (m)
Formel for $\varphi 1$ = 109 × k × X1 × X2 × $\frac{\sqrt{r\ \times s}}{1}$ , (grader)
Faktor X1 tar man ut av en tabell med forholdet bredde/ dypgang, faktor X2 tar man ut av en tabell for CB, k tar man ut av en tabell som er beregnet etter formel = Ak ×100/ LWl ×B. (Ak er total areal av slingringskjøl, LWl er lengde i vannlineplan og B er bredde på spant, r = 0,73 + 0,6 OG/d der OG = KG – d (dypgang), s er faktor som man tar ut av en tabell på grunnlag av rulleperioden (T).
Fra lovdata: Forskrift om stabilitet, vanntett oppdeling og vanntette/værtette lukningsmidler på flyttbare innretninger
1. Generelle krav for innaktstabilitet.
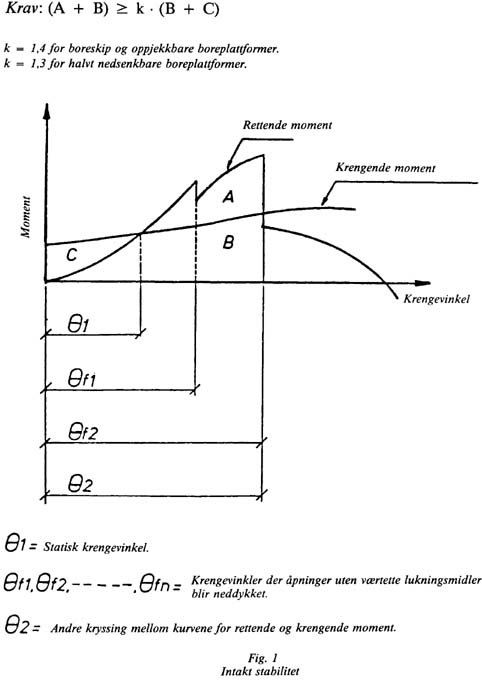
a) Statisk krengevinkel på grunn av vind (θ₁ ) skal i enhver tilstand ikke overstige 17°.
b) «Andre kryssing» mellom kurven for rettende moment og kurven for vindmoment (θ₂) skal skje ved en vinkel som er 30°, eller større. «Andre kryssing» er definert som det punkt der kurven for rettende moment korrigert for mulig progressiv fylling krysser kurven for vindmoment for annen gang.
c) Kurven for rettende moment skal være positiv over hele området fra opprett til andre kryssing.
2. Tilleggskrav for innretninger av skipstype og oppjekkbare innretninger:
a) Metasenterhøyden (GM) skal være 0,5 m eller større.
b) Arealet under kurven for rettende moment opptil «andre kryssing», eller eventuelt til en mindre vinkel, skal minst være 40% større enn arealet under kurven for vindmoment regnet opp til den samme begrensende vinkel.
3. Tilleggskrav for halvt nedsenkbare innretninger.
a) Metasenterhøyden (GM) skal være minst 1,0 m for alle operasjons- og forflytningstilstander samt sikkerhetstilstanden. Metasenterhøyden skal aldri være mindre enn 0,3 m i temporære tilstander.
b) Arealet under kurven for rettende moment opp til «andre kryssing», eller eventuelt til en mindre vinkel, skal minst være 30% større enn arealet under kurven for vindmoment begrenset av den samme vinkel.
4. Forutsatt at en tilsvarende standard av sikkerhet er opprettholdt, kan alternative intaktstabilitetskrav tillates av Sjøfartsdirektoratet, for eksempel basert på modellprøver, jf. § 4.
Legg merke til at kurvene er tegnet opp som moment og ikke som arm. Rettende moment: ∆ × rettende arm.
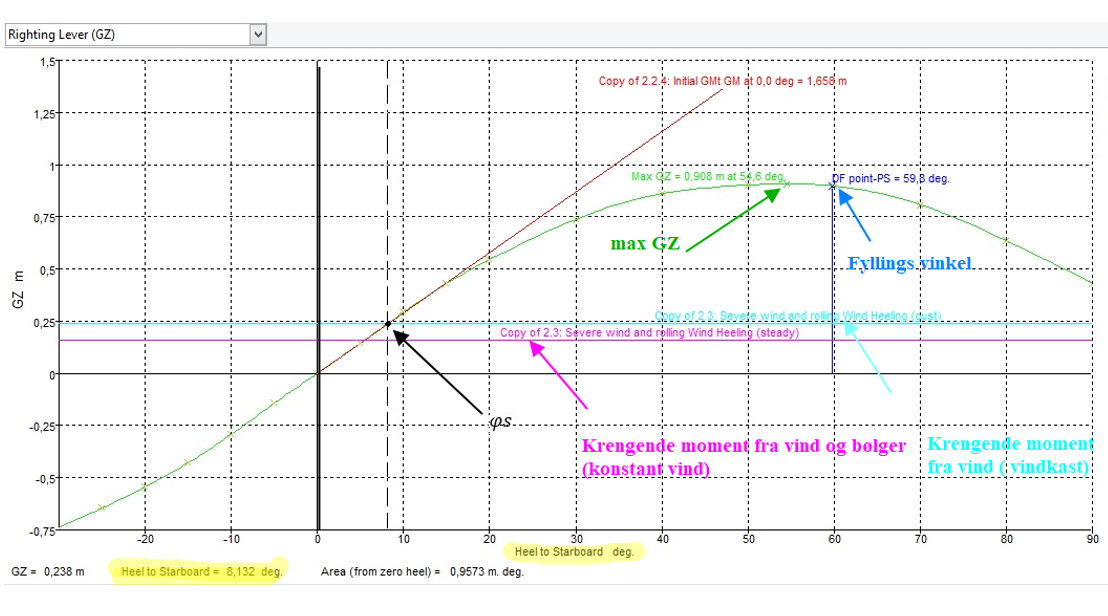
Figur 0277 GZ kurve med konstant vind, kastevind og fyllingsvinkel.
Fyllingsvinkel: Fyllingsvinkelen er den krengevinkel der den nederste kant av åpninger i skroget, overbygningen eller i dekkshus, som ikke kan lukkes værtett kommer under vann. Det er dette som gir begrensinger til «Si» (se kapittel 1 «probabilistiske metode»).

