Formelhefte – Funksjon 1: Navigering
VIKTIG!
Dette er 'online-versjonen' for mobil etc. Til eksamen, prøver o.l. må du bruke PDF-versjonen. Bruk lenkene oppe til høyre.
KAP. 1 DEFINISJONER
Storsirkel (great cicle)
er skjæringskurven mellomrom en kuleflate og ethvert plan gjennom kulens sentrum.
Småsirkel (small circle)
er skjæringskurven mellom en kuleflate og ethvert plan gjennom kulens sentrum.
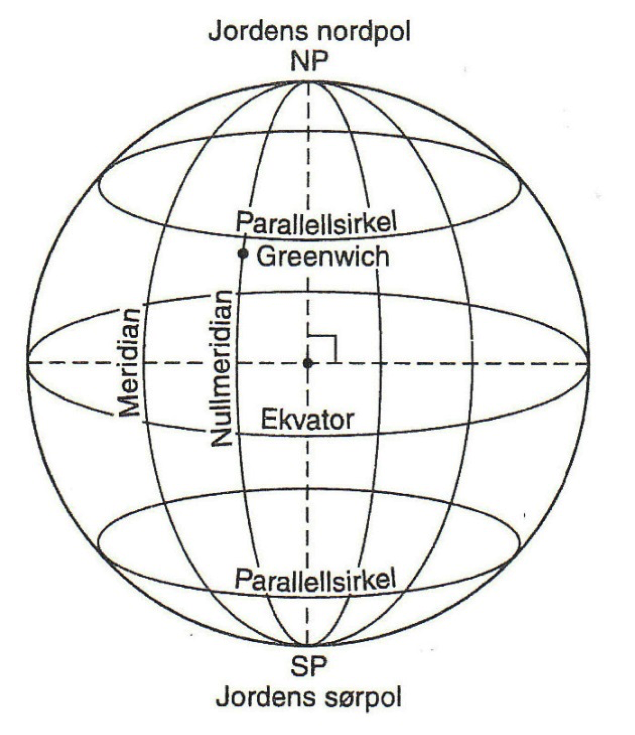
Meridian (meridian)
er storsirkelen gjennom jordens poler og storsirkelen gjennom himmelens nordpol og senit, eller himmelens sørpol og nadir.
Nullmeridian (prime meridian)
er storsirkelen gjennom jordens poler og den opprinnelige posisjonen til Greenwich-obervatoriet i London-bydelen Greenwich.
Ekvator (equator)
er storsirkelen på jorden hvis plan står vinkelrett på jordaksen og går midt mellom aksens to poler.
Parallellsirkel (parallel)
er småsirkelen som er parallell med ekvator.
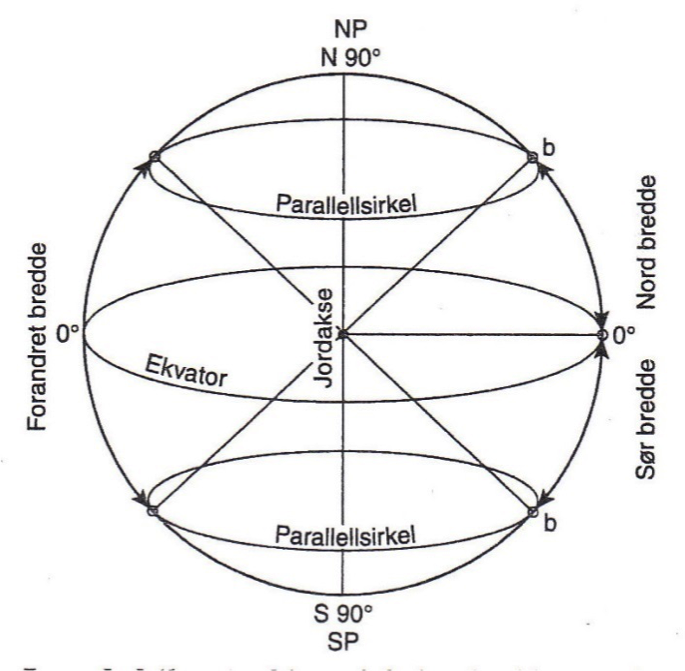
Bredde (b) (latitude)
er vinkelen (stykke av en meridian), målt nord (N) eller sør (S) fra ekvator, langs en meridian til stedets parallellsirkel.
δ bredde (bf) (difference of latitude)
forandret bredde mellom to steder er vinkelen (stykket av en hvilken som helst meridian) målt mellom stedenes parallellsirkler.
Lengde (longitude)
er vinkelen (stykket av ekvator), målt øst (E) eller vest (W) fra null-meridianen, langs ekvator.

δ lengde (lf) (difference of longitude)
forandret lengde mellom to steder er den minste vinkelen (det minste stykket av ekvator) målt langs ekvator, mellom stedenes meridianer.
Avvikning (a)
er avstanden mellom to meridianer, målt i nautiske mil langs middelbredde-parallelsirkelen som ligger mellom avfarende og påkommende steds meridianer.
Bestikkregning (dead reckoning)
er å bestemme en posisjon ved å flytte frem en kjent posisjon når styrt kurs og forventet fart gjennom vannet blir anvendt.
Bestikkplass
er en posisjon som er bestemt ved bestikkregning
Kap. 2 KURSRETTELSER
Jordmagnetisme og magnetkompassets innvirkning
MK Magnetisk kurs (magnetic course )
er vinkelen mellom et fartøys midtlinje og magnetisk nord–sør-linje
KK Kompasskurs (compass course)
er vinkelen mellom et fartøys midtlinje og styrekompassets
nord–sør-linje.
Deviasjon (deviation)
er vinkelen mellom magnetisk nord–sør-linje og styrekompassets
nord–sør-linje.
+ når styrekompassets nord–sør-linje ligger øst for magnetisk nord–sør-linje.
– når styrekompassets nord–sør-linje ligger vest for magnetisk nord–sør-linje.
Misvisning (magnetic variation)
er vinkelen mellom geografisk nord–sør-linje (meridian) og magnetisk nord–sør-linje.
+ når den magnetiske nord–sør-linjen ligger øst for den geografiske nord–sør-linjen.
– når den magnetiske nord–sør-linjen ligger vest for den geografiske nord–sør-linjen.
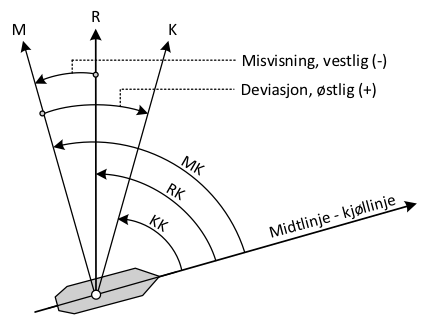
Kompasskursen (KK) er belastet med to avvik, deviasjon og misvisning, i forhold til rettvisende kurs (RK). Kalles «KK» for en «dårlig» kurs, og «RK» for en «god» kurs, gjelder følgende regel for kursrettelser:
- For kursrettelser fra «dårlig» (KK) til «god» kurs (RK), anvendes deviasjon og misvisning med sitt fortegn.
- For kursrettelser fra «god» (RK) til «dårlig» kurs (KK), anvendes fortegnene mot sitt fortegn.
Eksempel 1
| KK | = | 060° |
| deviasjon | = | + 10° |
| misvisning | = | – 5° |
| Rettvisende kurs: | ||
| KK | = | 060° |
| Dev. | = | + 10° |
| MK | = | 070° |
| Misv. | = | – 5° |
| RK | = | 065° |
Eksempel 2
| RK | = 065° |
| deviasjon | = + 10° |
| misvisning | = – 5° |
| Kompasskurs: | |
| RK | = 065° |
| Misv. (mot sitt fortegn) | = 5° |
| MK | = 070° |
| Dev. (mot sitt fortegn) | = + 1° |
| KK | = 060° |
Kap. 3 KURSER; VIND OG STRØM
Vindens innvirkning

K – Kurs (course)
er vinkelen mellom et fartøys midtlinje og en bestemt, nærmere angitt null-linje
RK – rettvisende kurs (true course)
er vinkelen mellom fartøyets midtlinje og geografisk nord–sør-linje.
RK styrt – rettvisende styrt kurs
er den retningen baugen peker i.
RK seilt – rettvisende seilt kurs
er den retningen fartøyet kommer frem gjennom vannet på grunn av sidevind.
Drift
er vinkelen mellom rettvisende styrt kurs og rettvisende seilt kurs.
Strømmens innvirkning
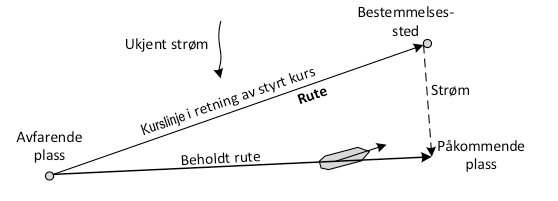
Rute (track)
er forventet horisontal retning mellom avfarende plass og
bestemmelsesstedet.
Beholdt rute (track made good)
er den rette linjen mellom avfarende plass og påkommende plass.
Vind og strøm
BK – Beholdt kurs (course made good)
er kurs over grunnen pga. både vindens og strømmens påvirkning.
Forventet beholdt kurs (course of advance)
er forventet kurs over grunnen.
Kap. 4 STRØMKOBLING
Strømkoblinger er å kombinere rettvisende seilt kurs med kjent strøm i farvannet, dersom denne er kjent. Det er vanligvis to problemer vi får å løse i forbindelse med strøm:
- Å finne skipets plass etter bestikk når vi tar hensyn til strømsettingen. Dette kalles rett strømkobling.
- Å finne rettvisende kurs vi må seile for å komme frem over grunnen i en bestemt retning når en kjenner strømmens retning og hastighet. Det kalles omvendt strømkobling.
Rett strømkobling
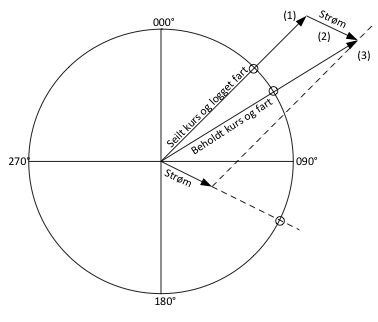
Omvendt strømkobling

Kap. 5 REGLER VED BRUK AV NAVIGASJONSFORMLENE PÅ ELEKTRONREGNER
Ved bruk av navigasjonsformlene på elektronregner gjelder følgende:
-
kurser entres med verdier fra 000° til 360°.
-
Dersom fortegnet (+) fremkommer i svaret eller entres i formlene, betyr det:
- nord bredde
- nord forandret bredde
- nord deklinasjon
- øst lengde
- øst forandret lengde -
Dersom fortegnet (-) fremkommer i svaret eller entres i formlene, betyr det:
- sør bredde
- sør forandret bredde
- sør deklinasjon
- vest lengde
- vest forandret blengde
Kap. 6 MIDDELBREDDESEILAS
Definisjoner
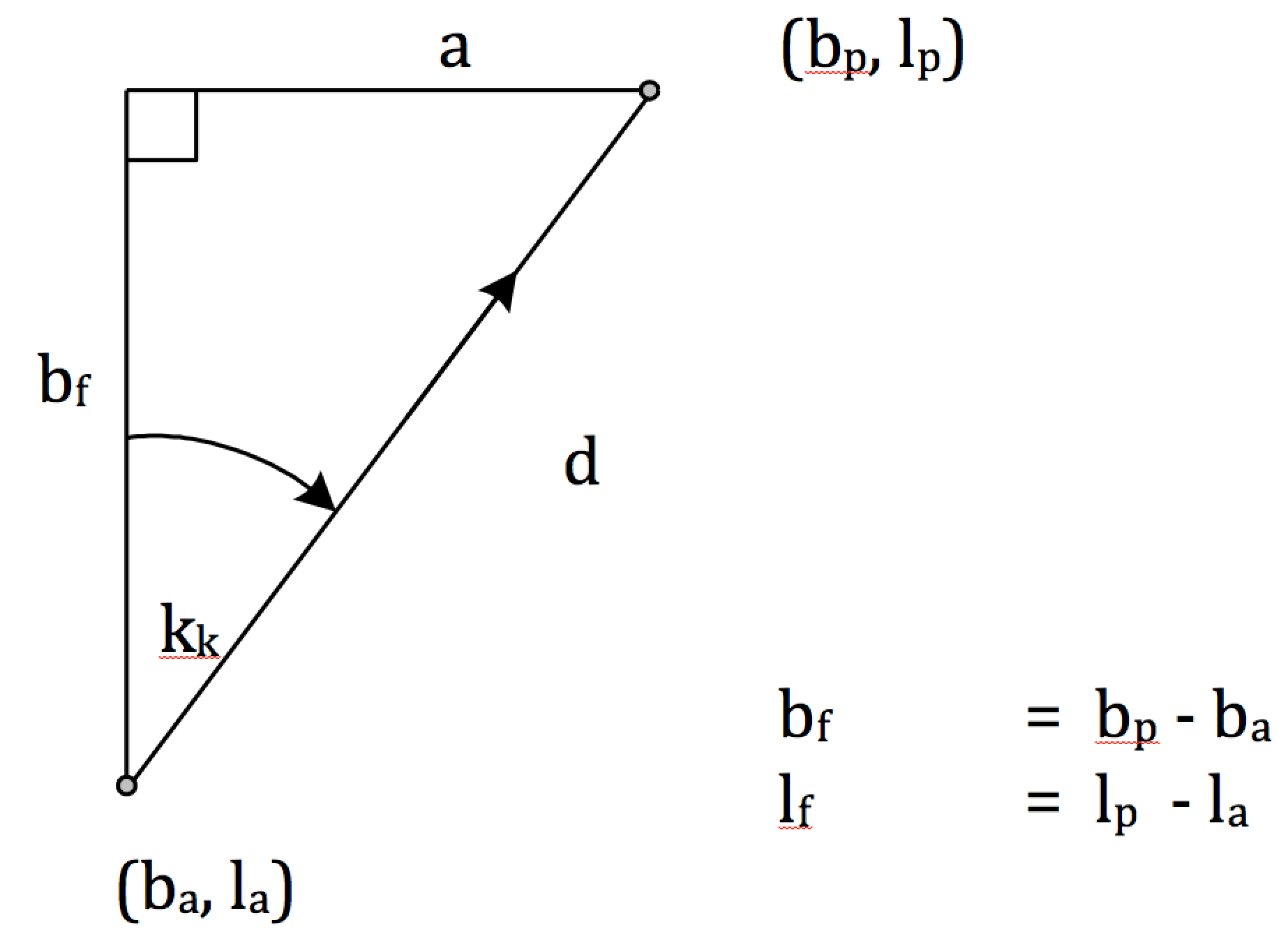
| ba | Avfarende bredde | (° og ‘) |
| bp | Påkommende bredde | (° og ‘) |
| bf | Forandret bredde | (° og ‘) |
| d | Distanse | (nm) |
| a | Avvikning | (nm) |
| lf | Forandret lengde | (° og ‘) |
| la | Avfarende lengde | (° og ‘) |
| lp | Påkommende lengde | (° og ‘) |
| kk | Kvadrantkurs | (0°–90°) |
Middelbredde
(ba ± bp)2 bm | Middelbredde | (° og ‘)
Forandret bredde og lengde
| bp | = | N/S (±) | ° | ' |
| bp | = | - N/S (±) | ° | ' |
| bf | = | N/S (±) | ° |
| l a | = | E/W (±) | ° | ' |
| lp | = | - E/W (±) | ° | ' |
| lf | = | E/W (±) | ° | ' |
Forandret bredde (N/S) og forandret lengde (E/W) angir i hvilken retning/kvadrant kursen ligger.
Kvadrantkurser
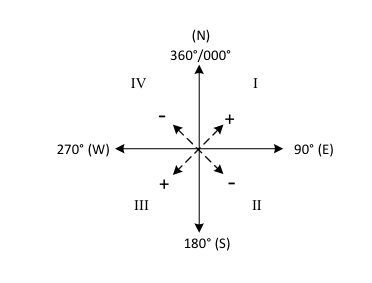
Rettvisende kurs finnes etter følgende regler, som er lik for N og S bredde.
Formlene gir seilasen retning ved hjelp av fortegnene.
Fortegn + ved: Nord (N) bredde og Øst (E) lengde
Fortegn – ved: Sør (S) bredde og Vest (W) lengde
Beregne kurs
a = lf • cos bm
tan kk = $\frac{a}{b_f}$
| a | Avvikning | (nm) |
| lf | Forandret lengde | (minutter) |
| bm | Middelbredde | (° og ‘) |
| kk | Kvadrantkurs | (0°- 90°) |
| bf | Forandret bredde | (minutter) |
Beregne distanse
d = $\sqrt{a^2+b^2_f}$
d = $\frac{b_f}{\cos k}$
d = $\frac{a}{\sin k}$
| d | Distanse | (nm) |
| k | 0°- 360°) | |
| bf | Bredde forandret (minutter) Formelen kan ikke brukes for kursene 090° og 270° |
|
| a | Avvikning Formelen kan ikke brukes for kursene 000° og 270° |
Beregne påkommende plass
bf = d • cos k
a = d • sin k
lf = $\frac{a}{\cos{b_m}}$
| bf | Forandret bredde | (minutter) |
| k | 0° – 360° | |
| d | Distanse | (nm) |
| a | Avvikning | (nm) |
| lf | Forandret lengde | (minutter) |
| bm | Middelbredde | (° og ‘) |
Kap. 7 MERKATORSEILAS
bu° = $\frac{180°}{\pi}\cdot\ln\tan{(45+\frac{b}{2})}$
bu' = bu° $\cdot$ 60
| bu° | Utvidede meridiangrader. + ved N bredde, - ved S bredde |
| bu’ | Utvidede meridianminutter. |
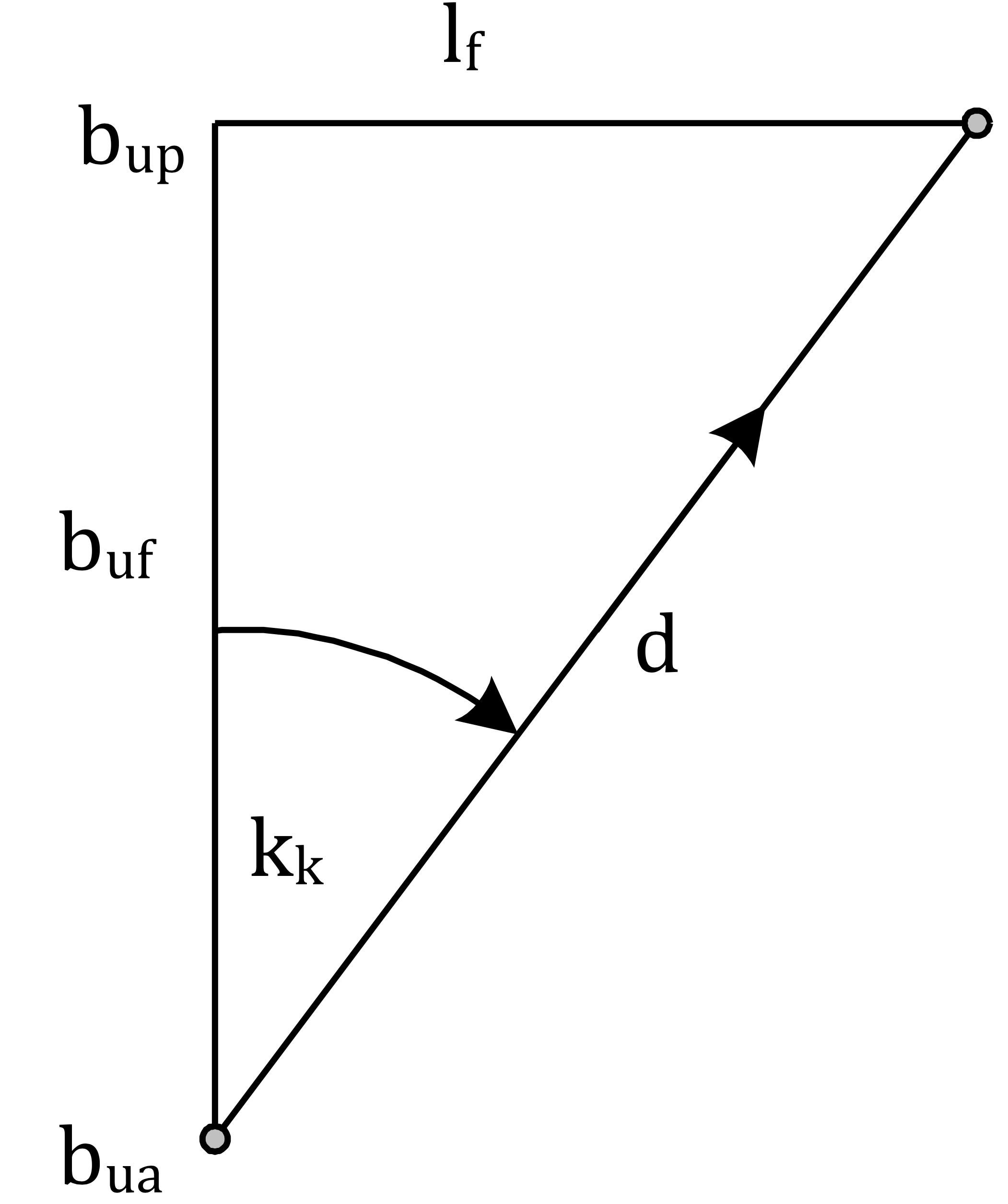
| bua | Utvidet avfarende bredde | (ekvatorminutter) |
| bup | Utvidet påkommende bredde | (ekvatorminutter) |
| buf | Utvidet forandret bredde | (ekvatorminutter) |
| lf | Forandret lengde (ekvatorminutter) | |
| d | Distanse | (nautiske mil) |
| kk | Kvadrantkurs | (0° – 90°) |
Forandret bredde og lengde
Verdiene entres med fortegn:
+ ved Nord (N) bredde og Øst (E) lengde
− ved Sør (S) bredde og Vest (W) lengde
| b p | N/S ) | (±) | ° | ' |
| b a | N/S | (±) | ° | ' |
| b f | N/S | (±) | ° | ' |
| b up | = ± | ‘ | ||
| b ua | = ± | ‘ | ||
| b uf | = ± | ‘ | ||
| l p | E/W | (±) | ° | ' |
| l a | E/W | (±) | ° | ' |
| l f | E/W | (±) | ° | ' |
Forandret bredde (N/S) og forandret lengde (E/W) angir i hvilken retning/kvadrant kursen ligger.
Kvadrantkurser
Se Middelbreddeseilas
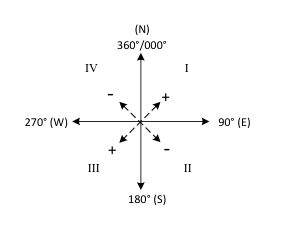
Rettvisende kurs finnes etter følgende regler, som er lik for N og S bredde.
Formlene gir seilasen retning ved hjelp av fortegnene.
Fortegn + ved: Nord (N) bredde og Øst (E) lengde
Fortegn – ved: Sør (S) bredde og Vest (W) lengde
Kurs og distanse
tan kk = $\frac{l_f}{b_{uf}}$
cos kk = $\frac{b_{\text{uf}}}{\sqrt{(l_{\text{f}}^{2}+b_{\text{uf}}^{2})}}$
d = $\frac{b_{f}}{\cos k}$
| kk | Kvadrantkurs | (0° – 90°) |
| lf | Forandret lengde | (minutter) |
| buf | Utvidet forandret bredde | (minutter) |
| d | Distanse | (nm) |
| bf | Forandret bredde | (minutter) |
| k | 0°–360° | (alle desimaler!) |
Forandret lengde
l f = buf • tan k
| lf | Forandret lengde | (minutter) |
| buf | Utvidet forandret bredde | (minutter) |
| k | 0°–360° | (alle desimaler!) |
Kap. 8 STORSIRKELSEILAS
Nord bredde

| Vertex | Storsirkelens høyeste bredde. |
| ba | Bredde avfarende |
| la | Lengde avfarende |
| bv | Bredde vertex |
| lfv | Lengdeforandring til Vertex. |
| bp | Bredde påkommende |
| lp | Lengde påkommende |
Forandret bredde og lengde
Verdiene entres med fortegn:
+ ved Nord (N) bredde og Øst (E) lengde
− ved Sør (S) bredde og Vest (W) lengde
| bp | = | N/S (±) | ° | ‘ | lp | = | E/W (±) | ° | ‘ |
| ba | = | - N/S (±) | ° | ‘ | la | = | - E/W (±) | ° | ‘ |
| bf | = | N/S (±) | ° | ‘ | lf | = | E/W (±) | ° | ‘ |
Kvadrantkurser
Se Middelbredde- og Mercatorseilas
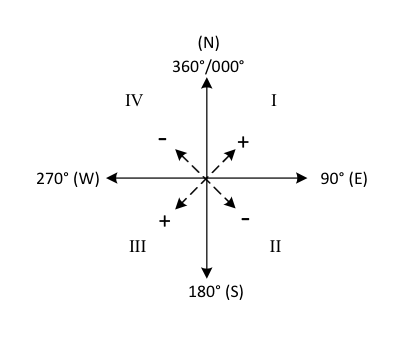
Rettvisende kurs finnes etter følgende regler, som er lik for N og S bredde.
Formlene gir seilasen retning ved hjelp av fortegnene.
Fortegn + ved: Nord (N) bredde Øst (E) lengde
Fortegn - ved: Sør (S) bredde Vest (W) lengde
Begynnelseskurs
tan kk = $\frac{\sin{l_f}}{(\tan{b_p}\cdot\cos{b_a}-\sin{b_a}\cdot\cos{l_f}}$
| kk | Kvadrantkurs | (0°–90°) |
Storsirkeldistanse
cos d =sin ba • sin bp + cos ba • cos bp • cos lf
| d | Distanse | (° og ‘) |
| d | ° 60’ | (nm) |
Kurs når distansen er kjent
cos k = $\frac{(\sin{b_p-\sin{{b_a}\cdot \cos{d)}}}}{\cos{{b_a} \cdot \sin{d}}}$
| k | Begynnelseskurs | (0° – 180°) |
| Seilas østover : k = k | ||
| Seilas vestover: k = (360 – k) |
Vertekspunktet
cos bv = sin kk⋅ cos ba
cos lfv = $\frac{\cos b_{a}}{\tan b_{v}}$
sin dv = sin lfv • cos ba
| bv | Bredde verteks | (° og ‘) |
| lfv | Forandret lengde til verteks | (° og ‘) |
| dv | Distanse til verteks | (nm) |
Mellompunkt
tan bm = cos lfvm • tan bv
cos lfvm = $\frac{\tan{b_m}}{\tan{b_v}}$
| bm | Mellompunktets bredde | (° og ‘) |
| lfv | Forandret lengde til verteks | (° og ‘) |
| bv | Bredde verteks | (° og ‘) |
| lfvm | Forandret lengde fra verteks | (° og ‘) |
| Valgt lengde | lv | cos lfv | tan bv | tan bm |
|---|---|---|---|---|
| (valg) | (konstant) | ? | (konstant) | ? |
| « | « | ? | « | ? |
| « | « | ? | « | ? |
Distanse og tid til 1° kursforandring
d 1° = $\frac{60}{tan(b_{a} + 0,2\cdot\text{v}\cdot\cos{k)\cdot\sin{k}}}$
h 1° = $\frac{60}{\text{v}\cdot\tan(b_{a} + 0,2\cdot\text{v}\cdot\cos{k)\cdot\sin{k}}}$
| d 1° | Distanse til 1° kursforandring (ba + 0,2 • v • cos k) svarer til middelbredden for 24 timer |
(nm) |
| h 1° | Timer til 1° kursforandring Formlene gjelder ikke for middelbredde 0° |
Kap. 9 SAMMENSATT SEILAS
Nord bredde

Verteks lengde
cos lfv = $\frac{\tan b_a}{\tan b_v}$
| lfv | Forandret lengde til verteks | (° og ‘) |
| ba | Avfarende bredde | (° og ‘) |
| bv | Høyeste bredde (verteks) | (° og ‘) |
Begynnelseskurs
cos kk = sin lfv • sin bv
| kk | Begynnelseskurs Se «kvadrantkurser». |
(0–90°) |
Distanser
sin d = sin lfv• cos ba
dp = lfp • cos bv
| d | distanse | (nm) |
| dp | Distanse parallellsirkel | (nm) |
| fp | Lengdeforandring parallellsirkel | (minutter) |
| bv | Høyeste bredde (verteks) | (° og ‘) |
Kap. 10 ASSISTANSEKURS

- Sett ut peilelinjen mellom fartøyene.
- Sett ut andre fartøys kurs og fart.
- Sett ut egen fart fra andre fartøy til peilelinjen mellom skipene.
- Assistansekursen leses av.
tid =$\frac{\text(Avstand)}{\text(Relativ fart)}$
Kap. 11 ROR- OG PROPELLKREFTER
Rorkrefter

| V | Vannhastighet inn til roret. |
| P | Angrepspunkt for resultanten av de hydrodynamiske kreftene på roret. |
| Ø | Angrepsvinkel (rorvinkel). |
| L | Rorets løftekraft ("lift") |
| D | Rorets motstand ("drag") |
| R | Normalkraft på roret (loddrett på rorprofilet). |
Propellkrefter
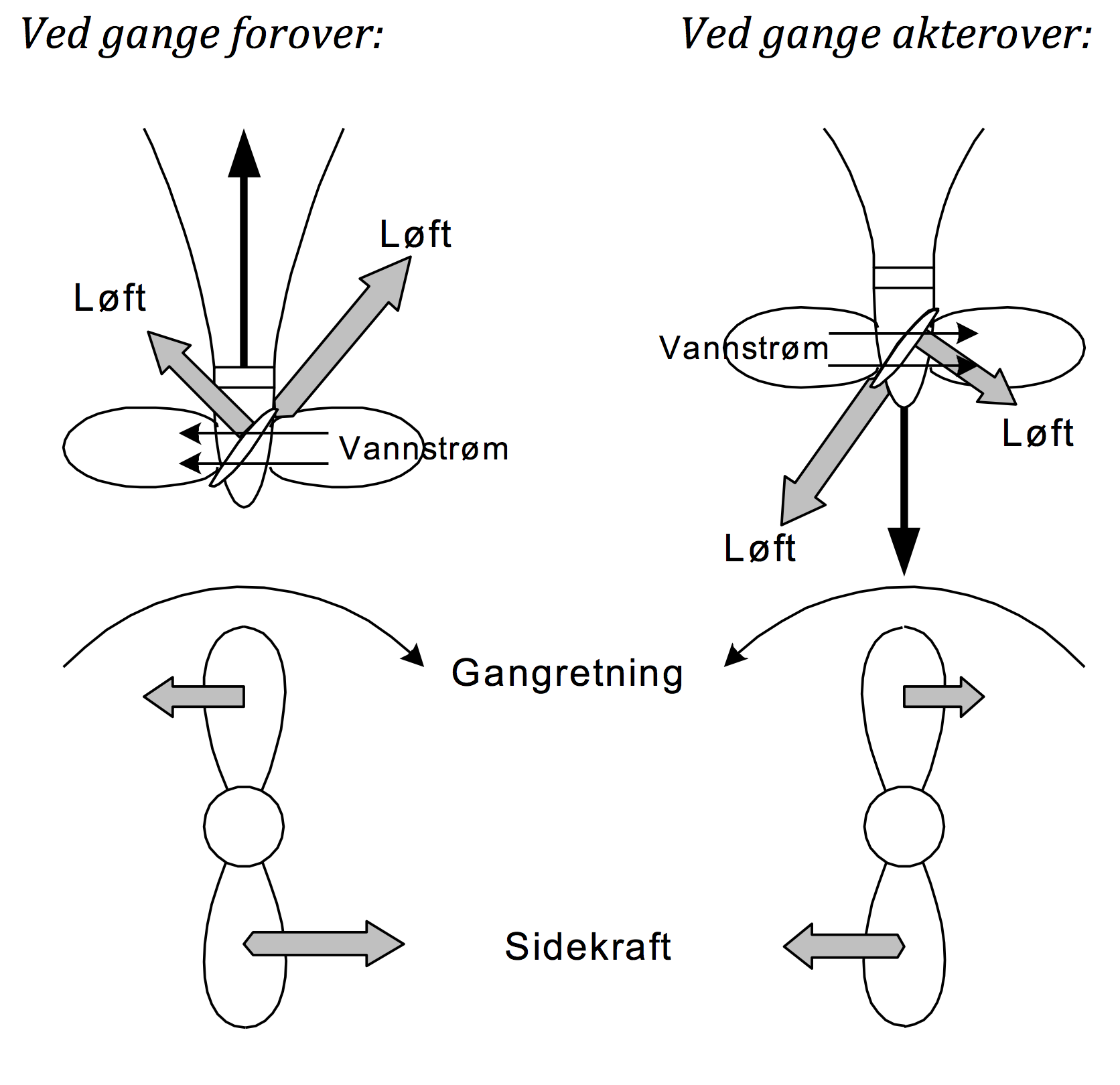
Skipets dreiesirkel
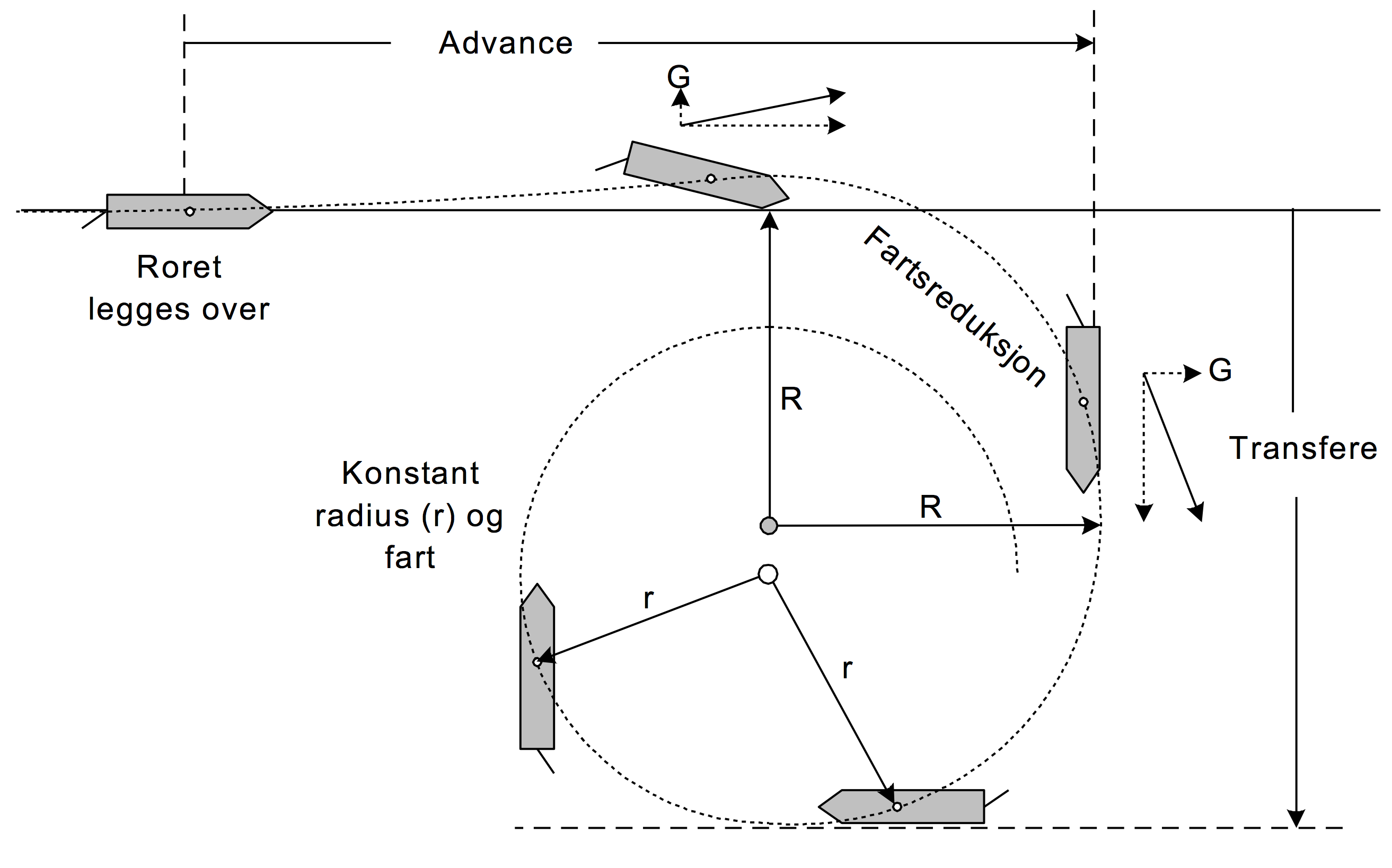
Sidekrefter under styrbord sving
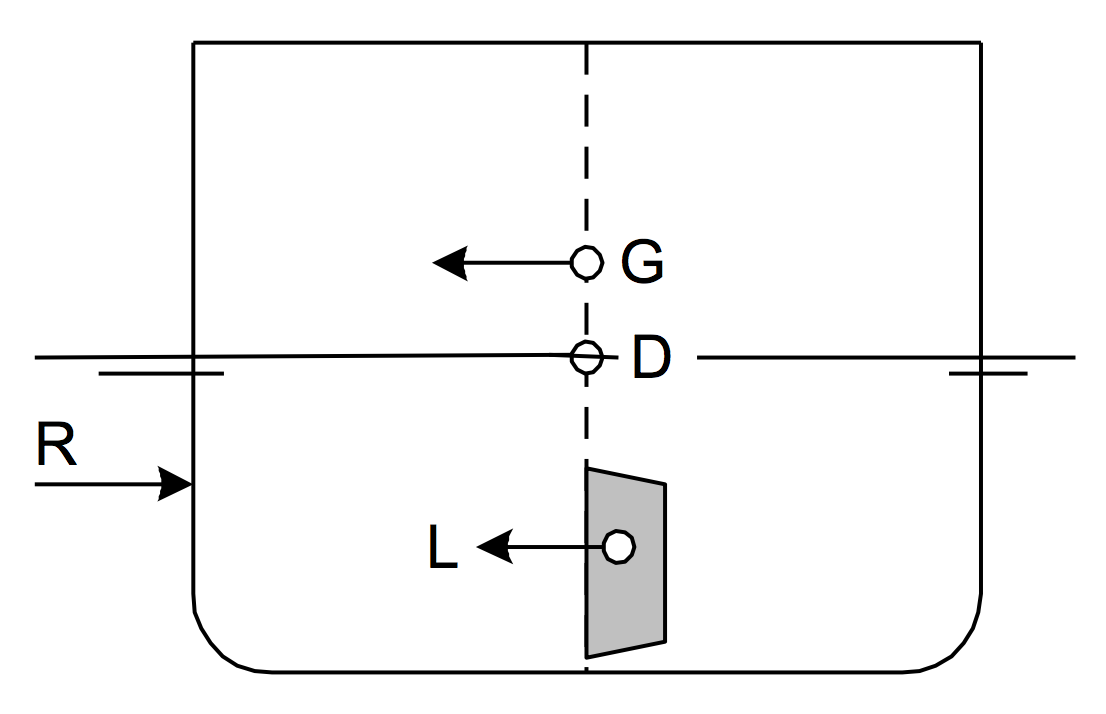
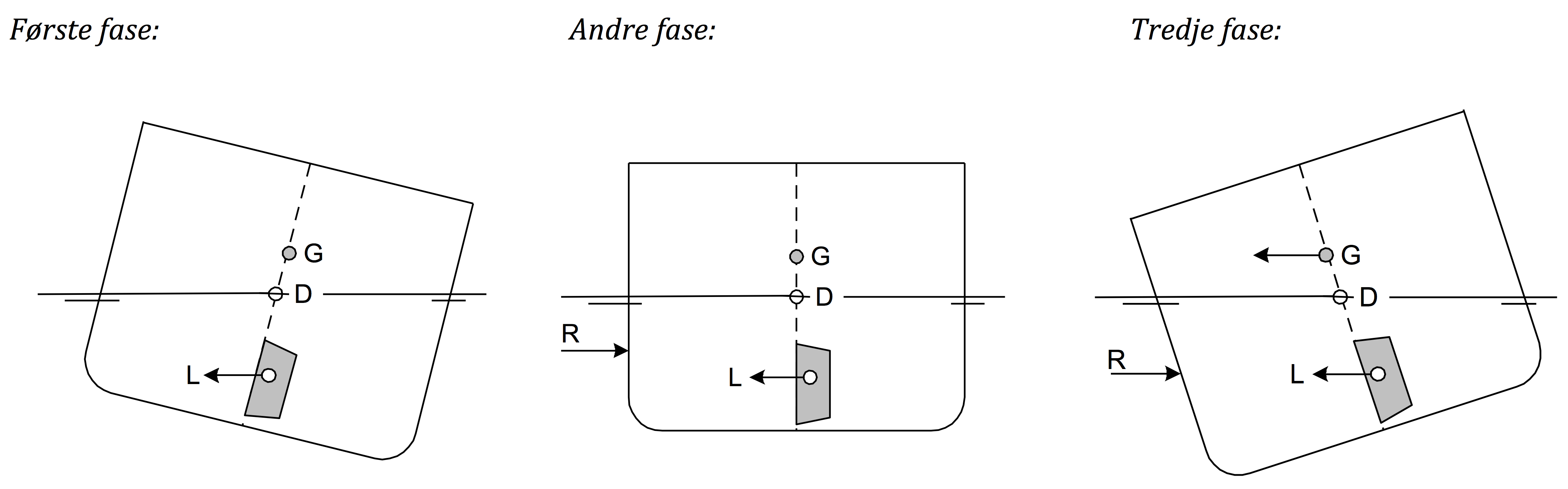
| G | Sentrifugalkraft |
| D | Dreiepunkt |
| L | Rorets løftekraft |
| R | Vannmotstand mot skutesiden |
Kap. 12 RATE OF TURN
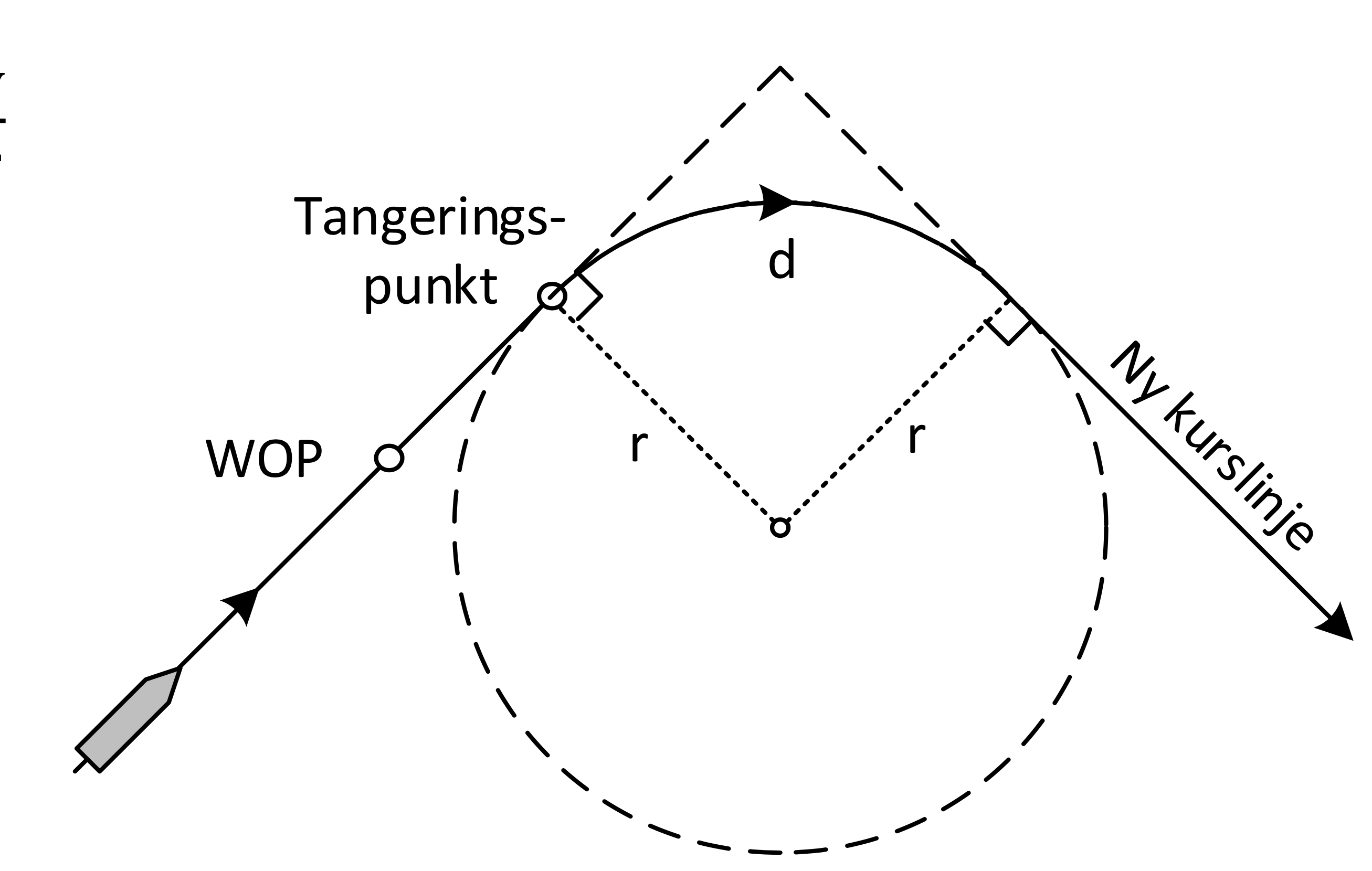
ROT ≈ $\frac{v}{r}$
| ROT | Grader pr. minutt |
| v | Fartøyets hastighet (knop) |
| r | Svingeradius (nm) |
Distanse i svingen
d = $\frac{2\pi\cdot\text{r}\cdot\text{δk}}{360}$
| d | Distanse i svingen | (nm) |
| δk | Kursforandring | (°) |
Tid i svingen
tid = $\frac{d}{v}$ ⋅ 60
| tid | (minutter) |
-
Kap. 13 SQUAT
Dypgangs- og trimforandring på dypt vann
Et skip under fart vil få en nedsynkning pga. den permanente bølgedalen skipet befinner seg i. I tillegg vil skipet får en trimforandring.
Dypgangs- og trimforandringen kalles «Squat».
Hvordan trimforandringen blir, er avhengig av skipets Cb, og på dypt
vann blir trimforandringen:
| Cb mellom 0,65-0,75 : | parallell nedsynkning |
| Cb større enn 0,75 : | forlig trimforandring, største dypgangsforandring forut |
| Cb mindre enn 0,65 : | akterlig trimforandring, største dypgangsforandring akter |
*Fyldig skip , Cb > 0,75 : *
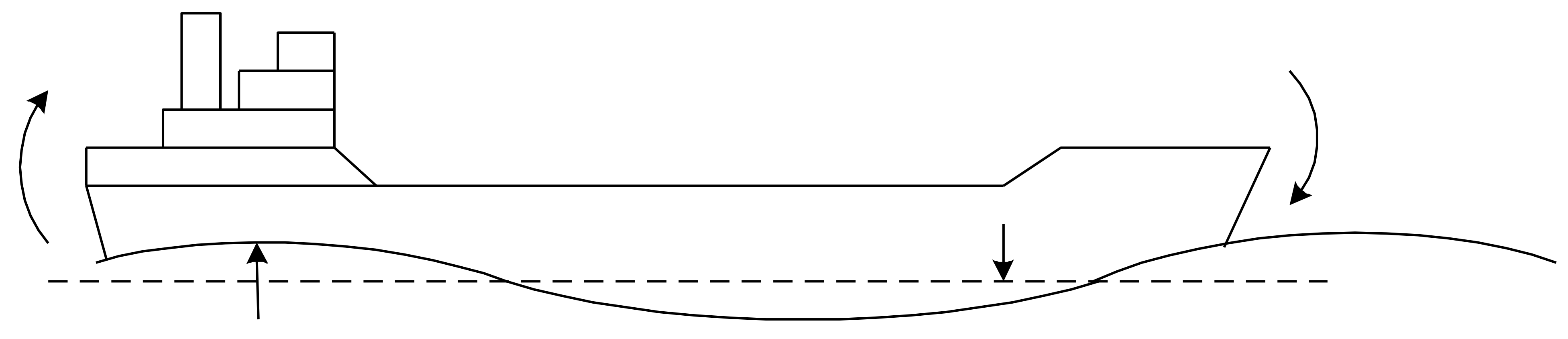
Her vil trimforandring bli farlig da skipet skyver bølgemønster forover.
Forskipet vil da ligge i den permanente bølgedalen.
*Slankt skip, Cb < 0,65 : *
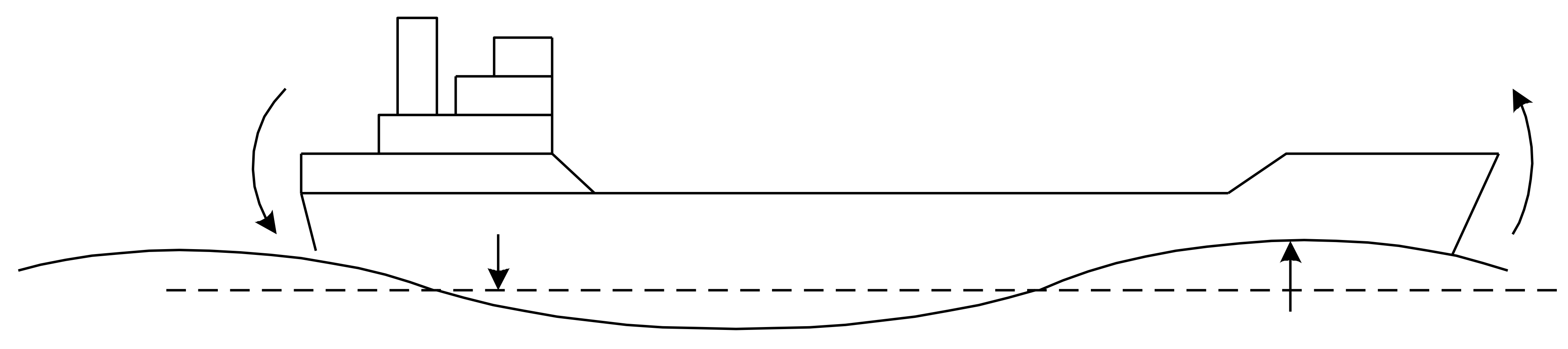
Skipet vil få en akterlig trimforandring da bølge-mønster trekkes akterover.
Akterskipet vil da ligge i den permanente bølge-dalen.
Dypgangs- og trimforandring på «grunt» vann
Grenseverdier for «grunt» vann
Når skipet kommer inn på «grunt» vann vil skipet få en dypgangs økning, og og generelt en forlig trimforandring.
Tabellen under viser grenseverdier fra skipet til «kanalveggen» hvor skipet begynner å bli påvirket:
Tabellen viser tenkte grenseverdier fra skipet til «kanalveggen» der skipet begynner å bli påvirket:
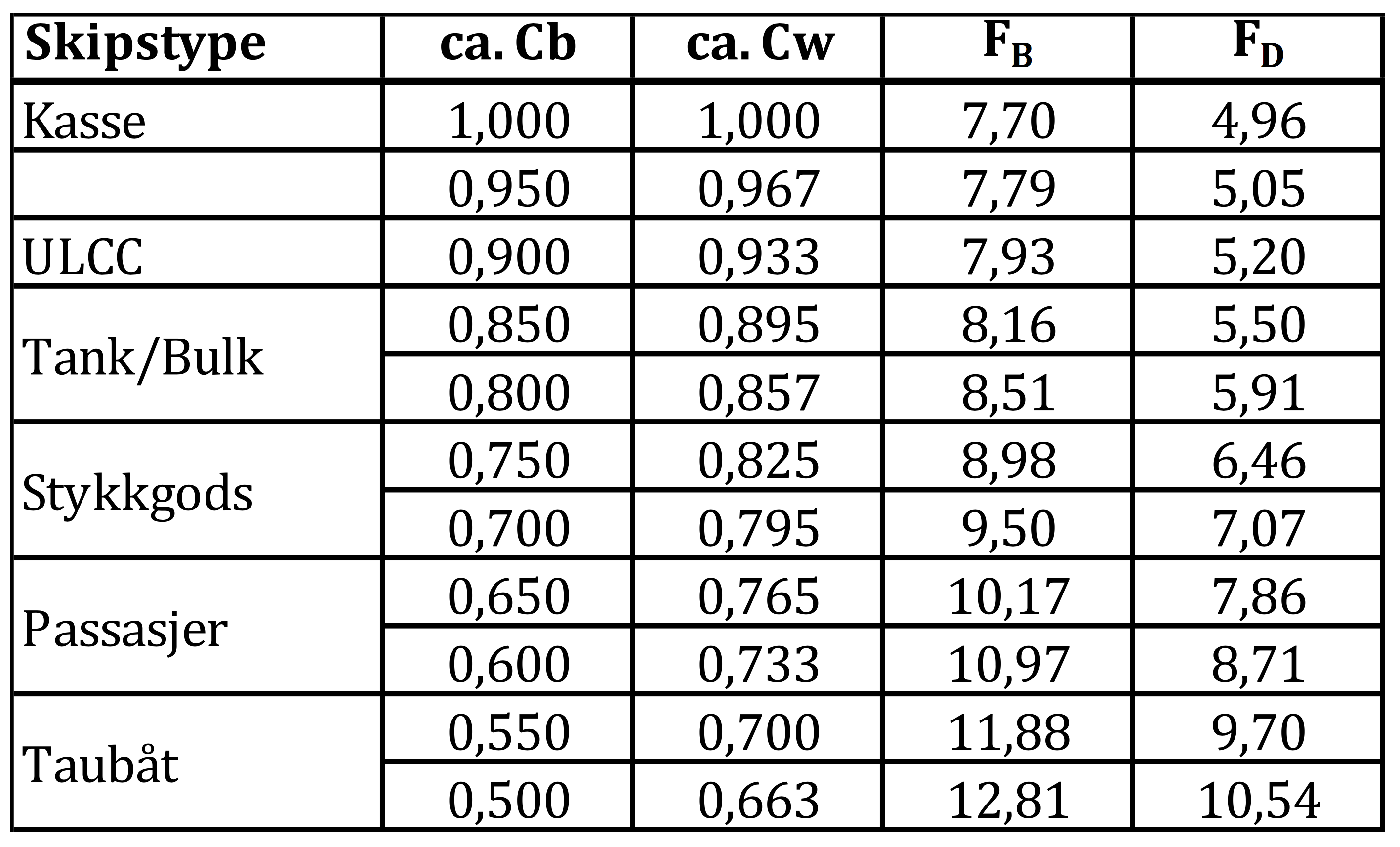
| FB | = B/b |
| B | Kanalbredde |
| b | Skipets bredde |
| FD | = D/d |
| H | Kanaldybde |
| d | Skipets dypgående |
«Åpen» kanal
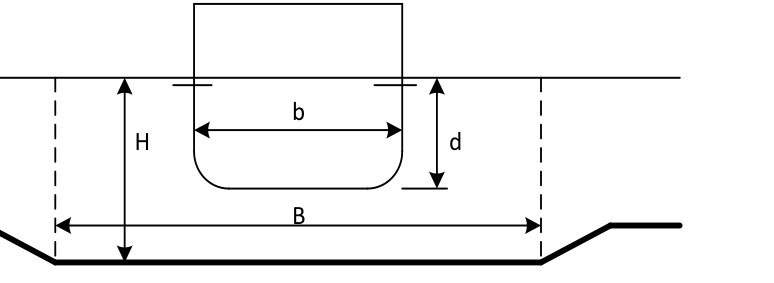
| B | Kanalens bredde | (m) |
| H | Kanalens dybde | (m) |
| b | Skipets bredde | (m) |
| d | Skipets dybde | (m) |
Blokkeringsfaktorer som bestemmer størrelsen på squat
FD = $\frac{H}{d}$
S1 = $\frac{1}{(F_{B}\cdot{F_D})}$
S2 = $\frac{1}{(1 - \ S_{1})}$
| FD | Beregnes ut fra kjente forhold |
| S1 | Blokkeringsfaktor |
| FB | Fra tabell foran |
| S2 | Blokkeringsfaktor |
Største dypgangsforandring
Squat = 1/30 ⋅ Cb ⋅ S22/3 ⋅ Vk2,08
Squat ≈ Cb ⋅ Vk2 • 0,01
Når H/d er mellom 1,1 og 1,4
| S2 | «Blokkeringsfaktor» |
| VK | Skipets hastighet (knop) |
«Lukket» kanal
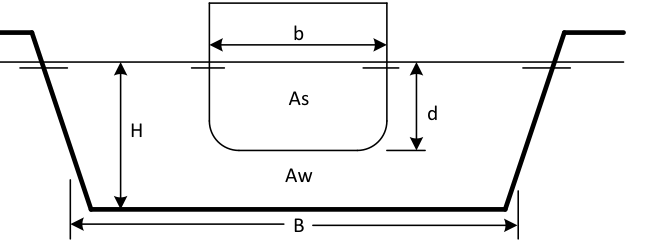
| Ac | H ⋅ B | Areal kanal | (m2) |
| As | d ⋅ b | Areal skip | (m2) |
| Aw | Ac – As | Areal vann | (m2) |
Blokkeringsfaktorer
S1 = $\frac{A_{S}}{A_{C}}$ = $\frac{d \cdot b}{H \cdot B}$
S2 = $\frac{A_{S}}{A_{W}}$ = $\frac{S_{1}}{(1-S_{1})}$
Største dypgangsforandring
Squat = 1/30 ⋅ Cb ⋅ S22/3 ⋅ Vk2,08
Squat ≈ 2 • Cb • Vk2 • 0,01
Når S2 er mellom 0,100 og 0,265
| Squat | Største nedsynkning (m) |
| S2 | “Blokkeringsfaktor” |
| VK | Skipets hastighet i knop |
«Limiting speed» i «lukket» kanal
VL = Fn ⋅ $\sqrt{\text{g ⋅ H}}$
| VL | «Limiting speed» Største oppnåelige hastighet i kanalen |
| H | Kanalens dybde |
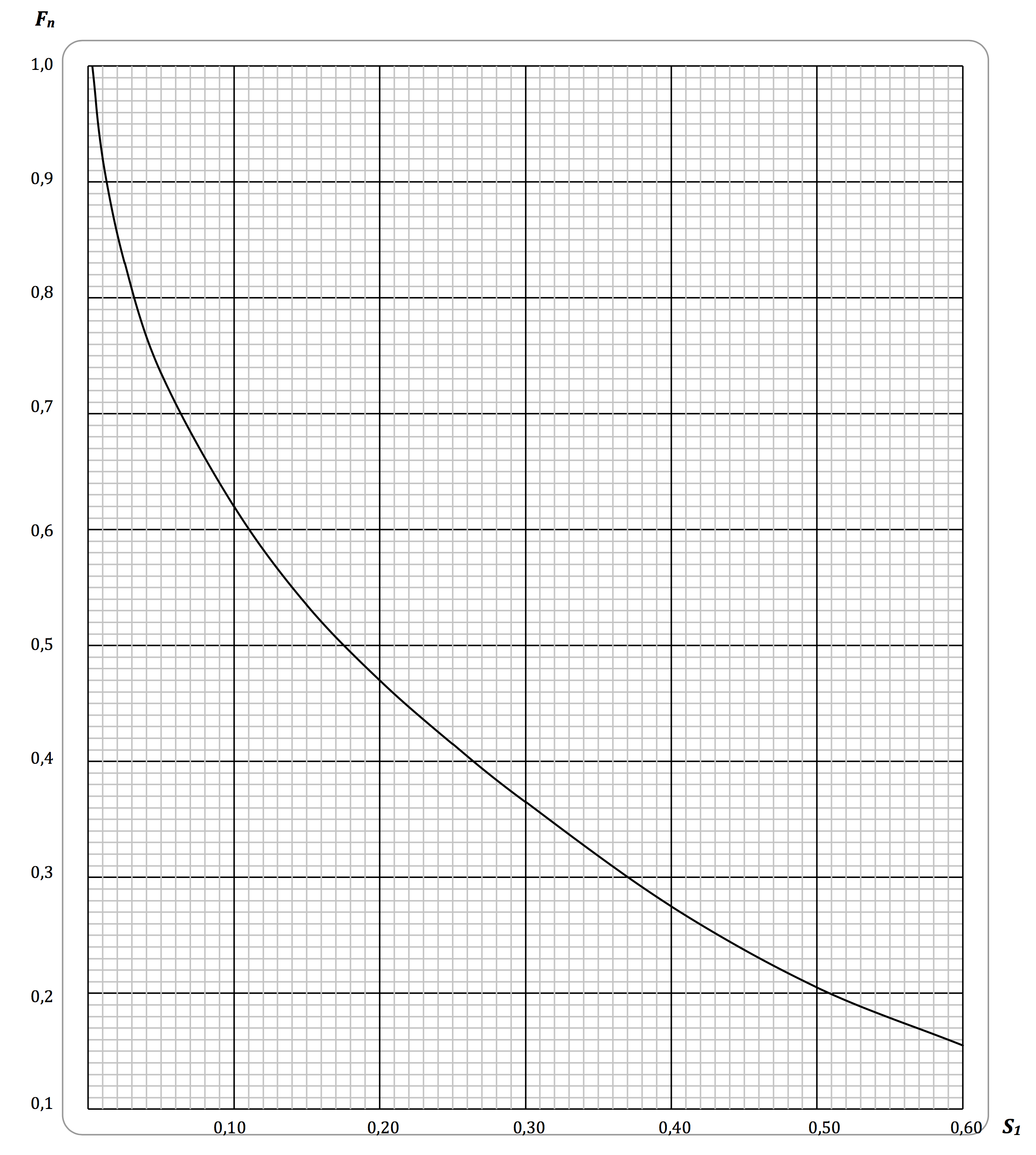
«Freuds number», Fn
I figuren går man inn med S1 på x-aksen. Trekk en vertikal opp til kurven, og fra skjæringspunktet går man horisontalt til venstre og leser av «Freuds number» (Fn)
Kap. 14 FORTØYNING
Vindkraftens virkning på fortøyning
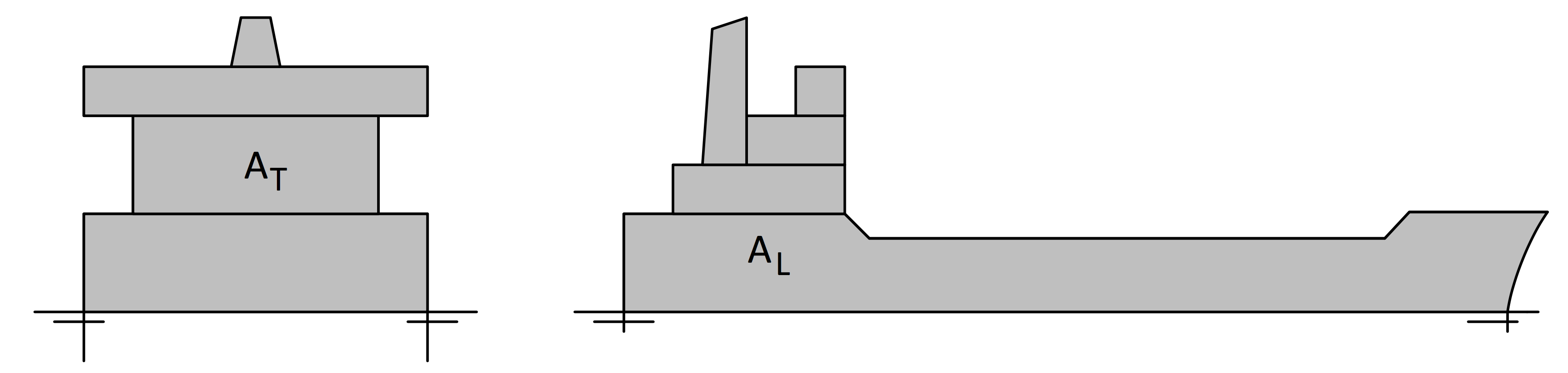
FV ≈ 0,135 ⋅ v2 ⋅ 10-3
| FV | Vindkraft | (t/m2) |
| v | Vindhastighet | (m/s) |
Fordeling av vindkraften
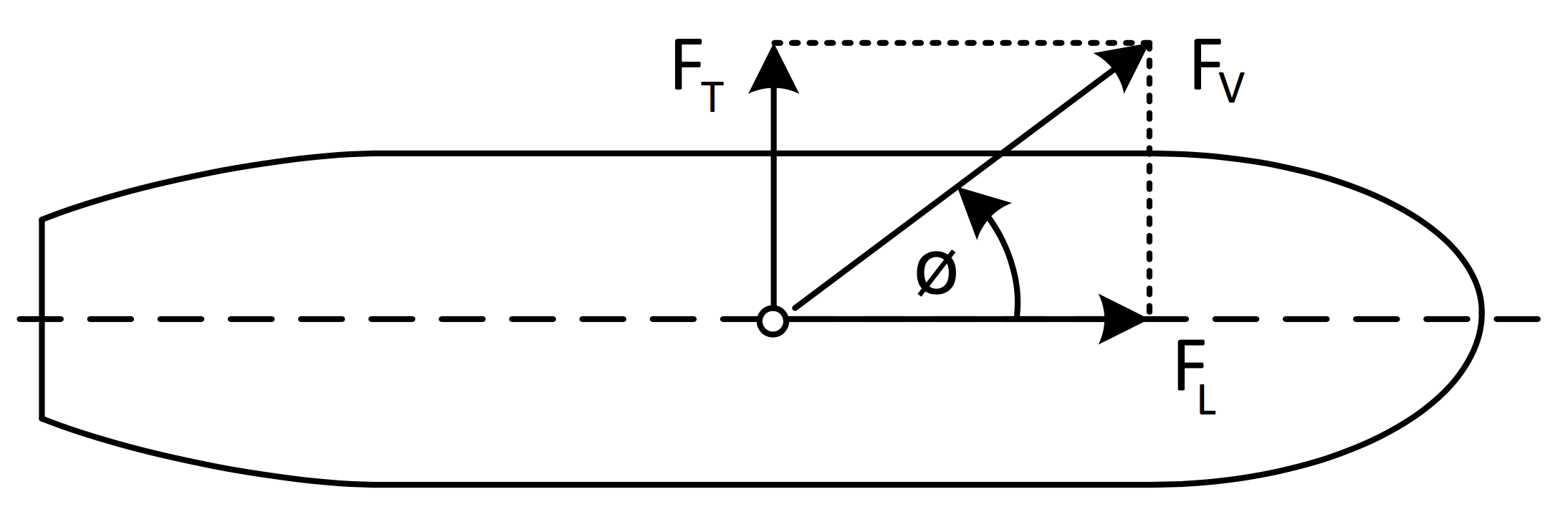
FT = FV ⋅ sin Ø ⋅ AL
FL = FV ⋅ cos Ø ⋅ AT
| FT | Tverrskips vindkraft | t2</sup |
| Ø | Vindens vinkel med langskipsplanet | |
| FL | Langskips vindkraft | t2</sup |
| AL | Langskips vindareal | (m2) |
| AT | Tverrskips vindareal | (m2) |
Tverrskips kraft på fortøyningene
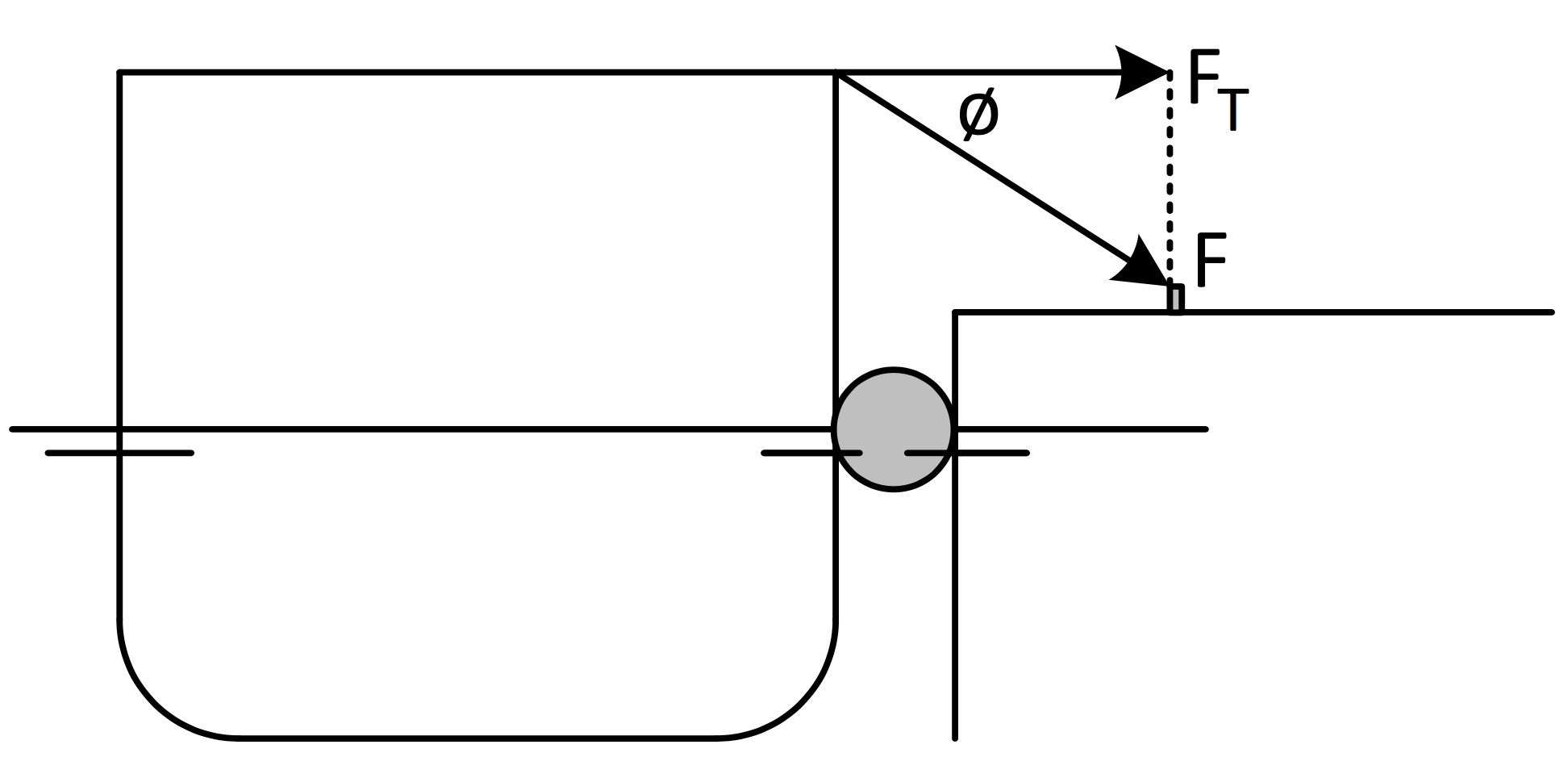
F = $\frac{F_{T}}{\cos Ø}$
| F | Kraft på fortøyning | t |
| FT | Tverrskips vindkraft | (t/m2) |
| Ø | Vinkel med horisont |
Langskips kraft på fortøyningene
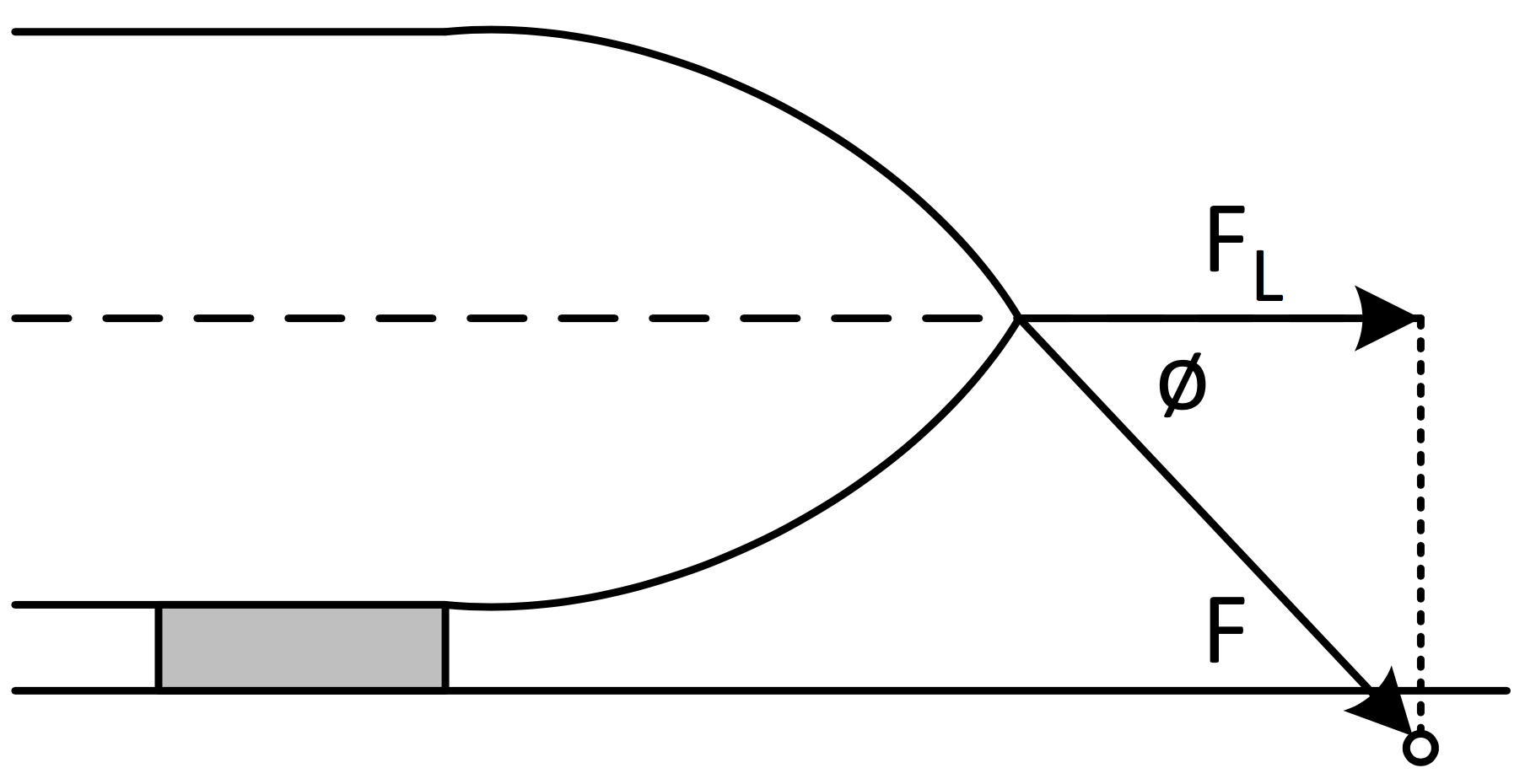
F = $\frac{F_{L}}{\cosα}$
| F | Kraft på fortøyning | t |
| FL | Langskips vindkraft | (t/m2) |
| Ø | Vinkel med langskipsretning |
Kap. 15 Astronomisk navigasjon; defenisjoner
Meridianfiguren
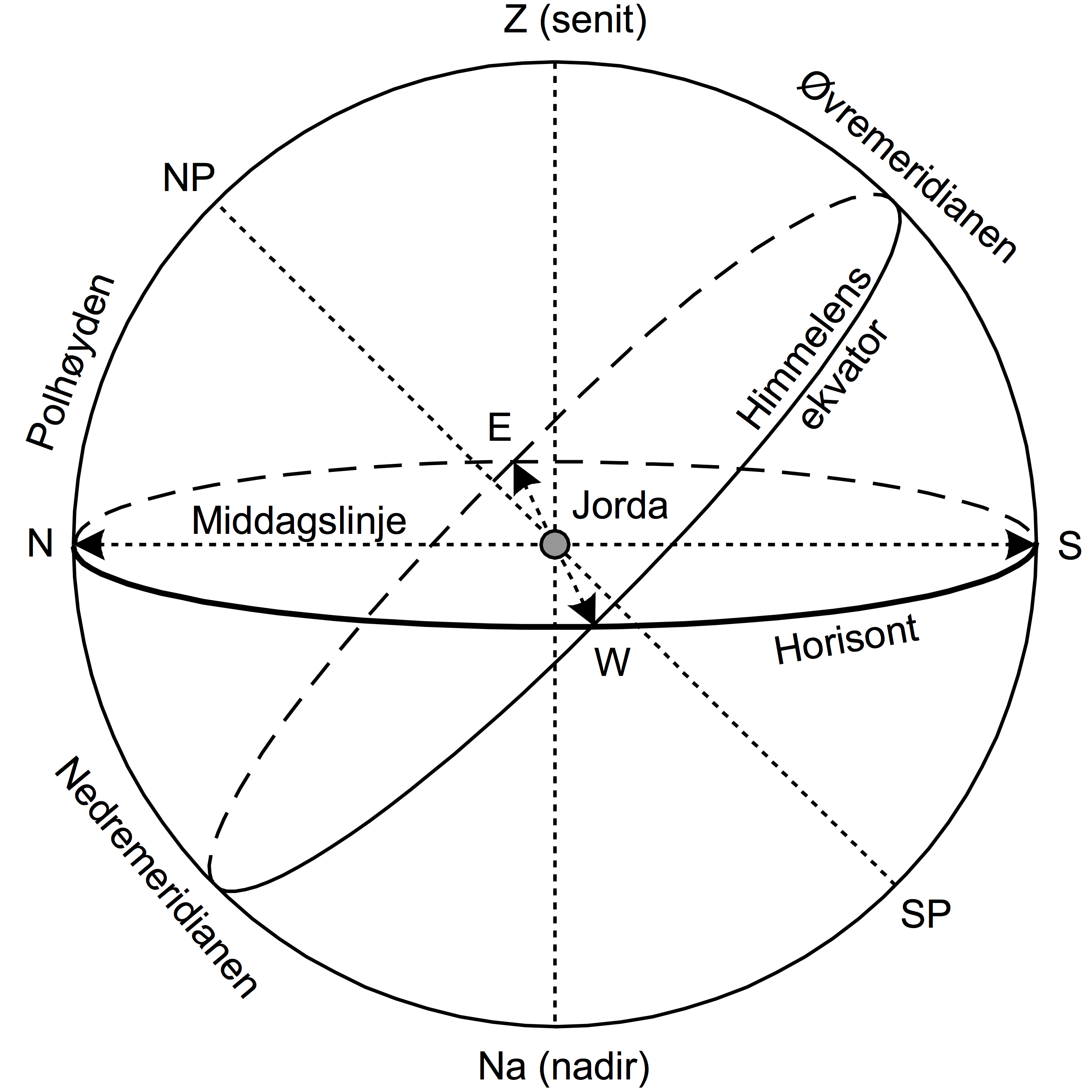
Himmelens ekvator
er storsirkelen hvor jordens ekvator-plan forlengde skjærer himmelkulen.
Himmelens poler (NP og SP)
Er forlengelsen av jordaksen.
Z (senit) og nadir (Na)
Er forlengelsen av loddlinjen gjennom observators ståsted.
Den sanne horisont
Er en storsirkel som ligger 90° fra senit og nadir.
Meridianen
Er storsirkelen gjennom himmelens poler.
Polhøyden
Er himmelens pol over horisonten, og er lik påværende bredde.
Solas posisjoner på himmelkula
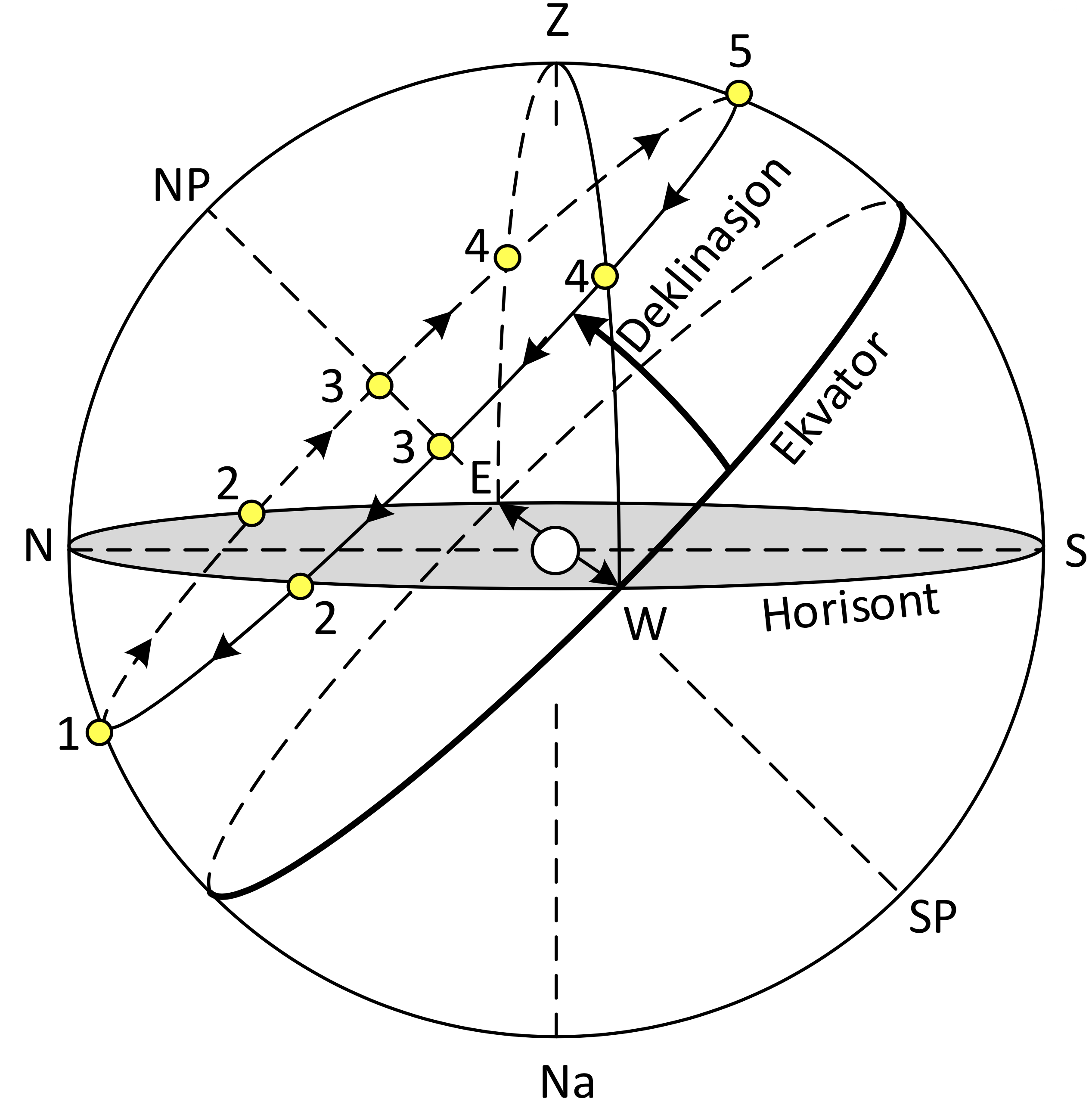
Solas dagsirkel
Sola beveger seg parallelt med ekvator og danner en sirkel i løpet av ett døgn.
Deklinasjon
Solas avstand fra ekvator, enten N eller S.
Kuliminasjon når sola er i N eller S
1. I nedremeridianen
5. I øvremeridianen
Opp- og nedgang
2. Når sola passerer den sanne horisont.
Halv nattbue
1.–2. Før soloppgang
2.–1. Etter solnedgang
Halv dagbue
2.–5. Mellom oppgang og øvremeridianen
5.–2. Mellom øvremeridianen og nedgang
Sekstimerssirkelen
3. Når sola passerer N–S-linjen
Vertikalsirkelen
4. Solas rettvisende peiling er enten 090° eller 270°.
Ekvatorsystemet
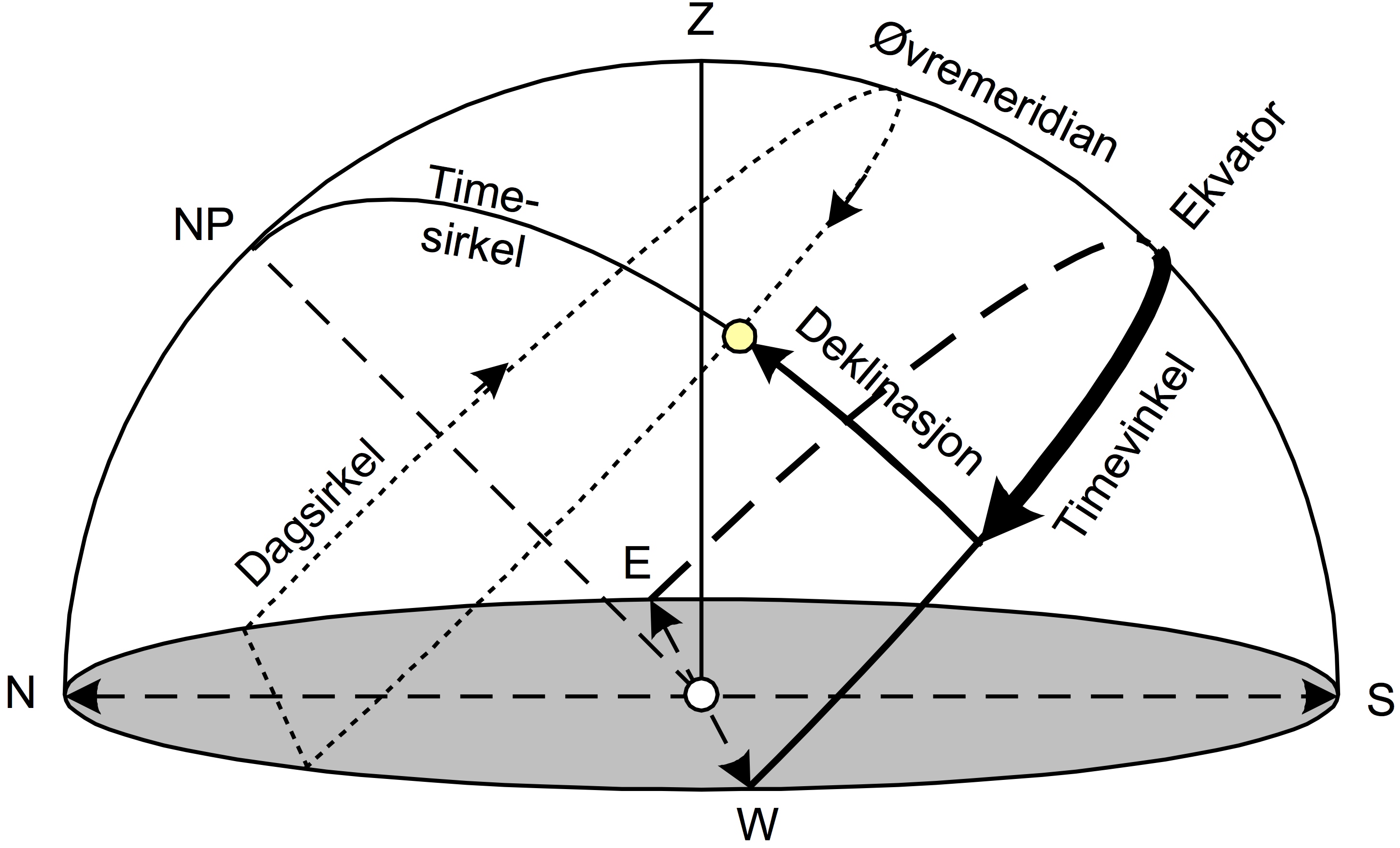
| GHA | Solas timevinkel vest for Greenwichmeridianen. | (° og ‘) |
| LHA | Solas lokale timevinkel vest for øvremeridianen (t). (LHA). | (° og ‘) |
| t | GHA ± W/E-lengde | |
| d | Deklinasjon | (° og ‘) |
Lokal timevinkel
LHA = GHA ± lengde
| + | ved E lengde | (° og ‘) |
| - | ved W lengde | (° og ‘) |
Horisontsystemet
Horisontsystemet
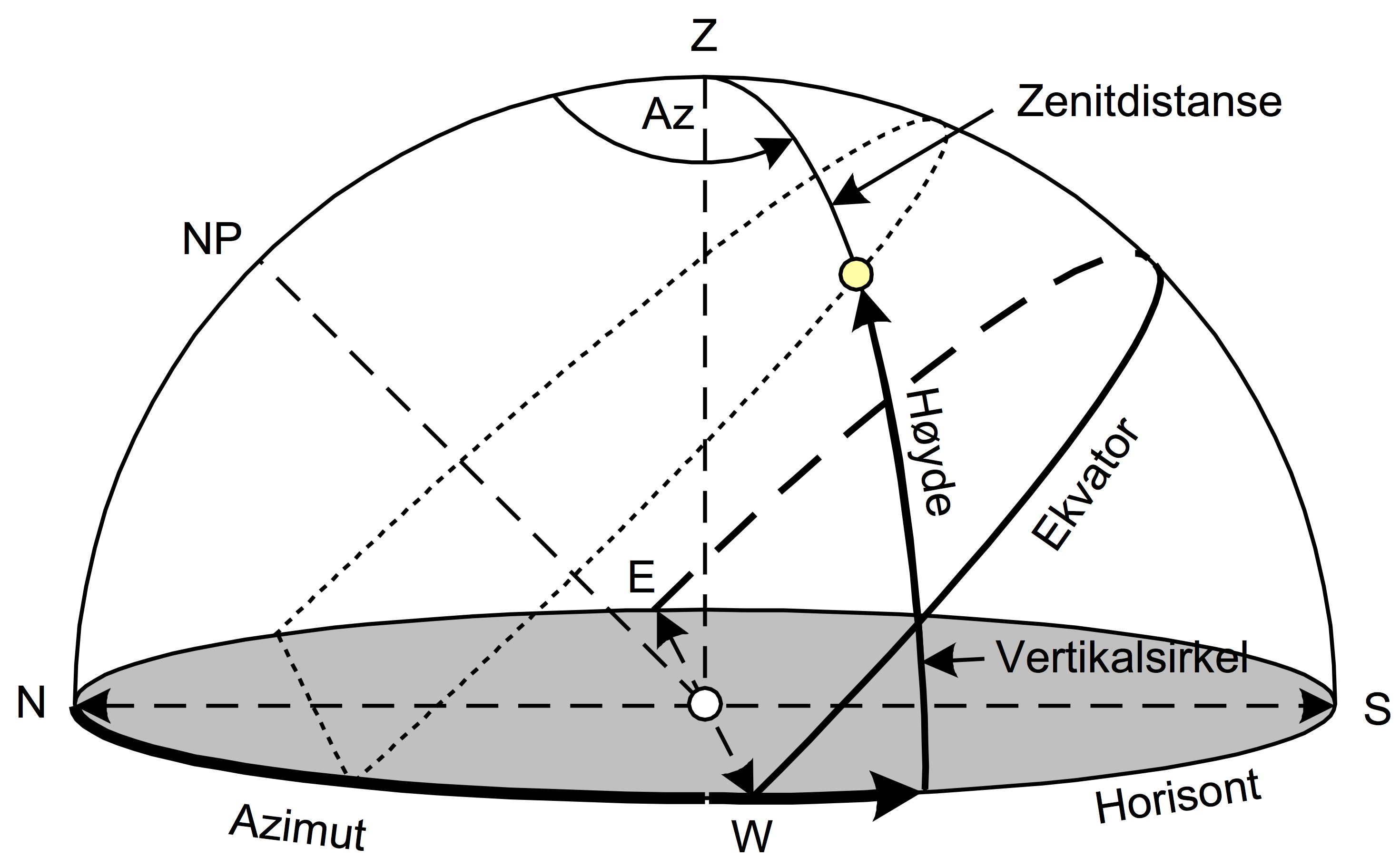
| h | Høyde, himmellegemets høyde over sanne horisont |
| Az (p) | Azimut, solas rettvisende peiling, regnet fra nord, både på nord og sør bredde. |
Posisjonstrekanten
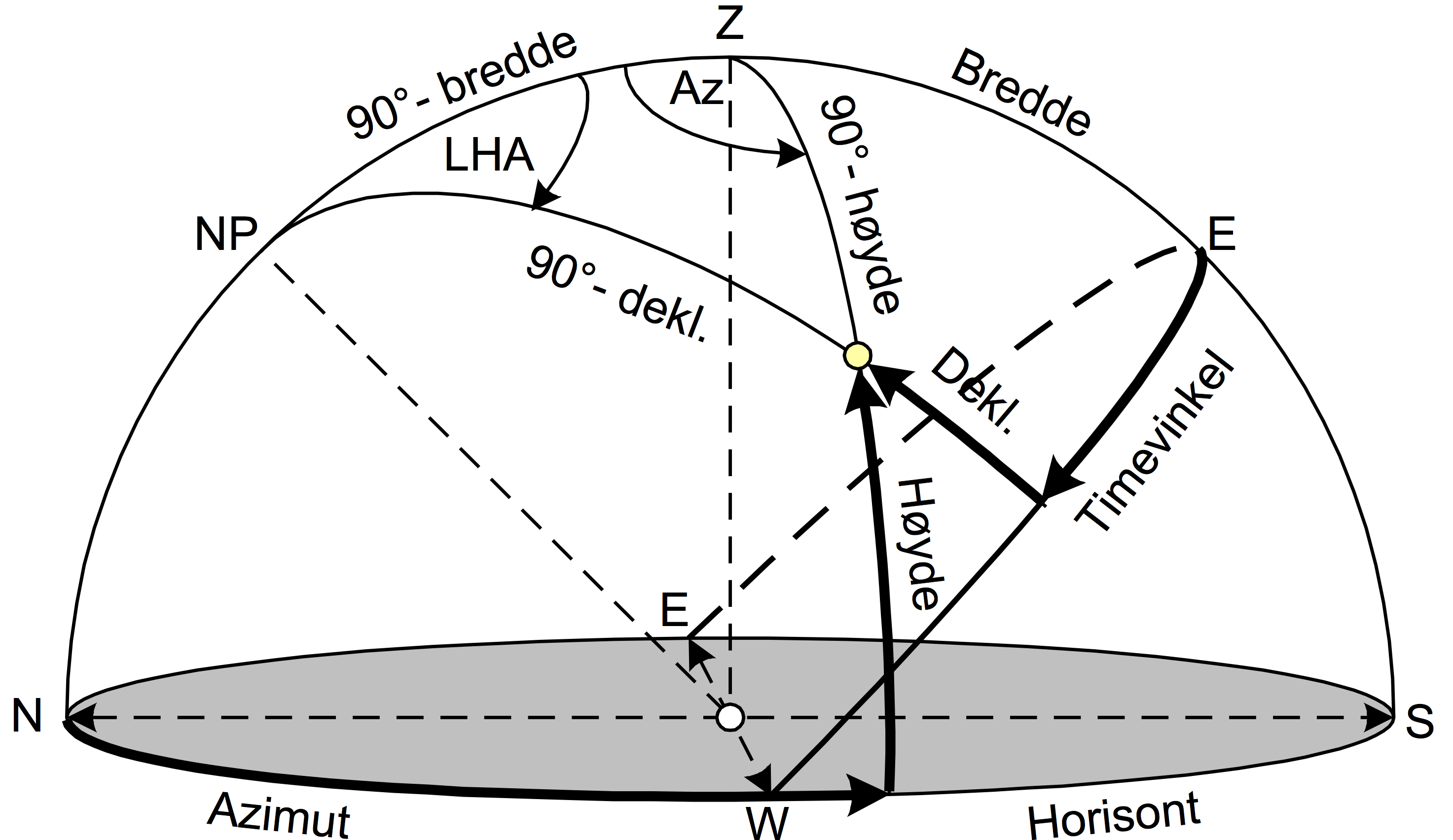
| b | Påværende bredde | (° og ‘) |
| l | Påværende lengde | (° og ‘) |
| t | Lokal timevinkel (LHA) | (° og ‘) |
| h | Solas høyde over horisonten | (° og ‘) |
| d | deklinasjon |
Kap. 16 HØYDEOBSERVASJONER
Posisjonstrekanten

| b | Påværende bredde | (° og ‘) |
| l | Påværende lengde | (° og ‘) |
| t | Lokal timevinkel (LHA) | (° og ‘) |
| h | Solas høyde over horisonten | (° og ‘) |
Posisjonsdata
Posisjon
LT og dato
Zone
| LT | Lokal tid |
Høydeformelen (ved høydeobservasjoner)
sin h = sin b ⋅ sin d + cos b ⋅ cos d ⋅ cos t
| h | Beregnet høyde | (° og ‘) |
| b | Påværende bredde | (° og ‘) |
| d | Deklinasjon | (° og ‘) |
| t | Lokal timevinkel vest (LHA) | (° og ‘) |
Høydeasimut (ved høydeobservasjoner)
cos Az = $\frac{(\sin{d-\sin{{b}\cdot\sin{h)}}}}{\cos{\text{b}\cdot\cos h}}$
| Az | Rettvisende peiling regnes fra nord, både på nord og sør bredde (0°-180°) |
| Rettvisende peiling er lik peiling (p) når lokal timevinkel (LHA) er mellom 180° og 360° Rettvisende peiling er lik (360° - p) når lokal timevinkel (LHA) er mellom 0° og 180° |
Høydeformel når himmellegemet er i meridianen
sin h = sin b ⋅ sin d + cos b ⋅ cos d ⋅ ± 1
| h | Høyde ved meridianpassasje | (° og ‘) |
| LHA (t) | er 000° i øvremeridianen (+). | |
| LHA (t) | er 180° i nedremeridianen (-). |
Ukjent stjerne
sin d = sin b ⋅ sin h + cos b ⋅ cos h ⋅ cos pr
| d | Stjernens deklinasjon | (° og ‘) |
| b | Påværende | bredde |
| h | Stjernens høyde | (° og ‘) |
| pr | Himmellegemets rettvisende peiling | (0° -360°) |
Kap. 17 TID TIL OBSERVASJONER
Sola i meridianen på sitt høyeste
| ¤ i mer. LMT | = | . |
| rett. lengde | = ± | . |
| ¤ i mer. UTC | = | |
| sone | = ± | . |
| ¤ i mer. LT | = | . |
| Kl. om bord | = | . |
| Tid til ¤ i mer. | = | . |
Tussmørket (Civil Twilight)/ Sol opp/ned
| «C.T.» ¤ | = | |
| rett. dag | = | |
| rett. breddel | = | |
| «C.T.» ¤ LMT | = | |
| rett lengde | = | |
| «C.T.» ¤ UTC | = | |
| Zone | = | |
| «C.T.» ¤ omb | = | |
| Kl. om bord | = | |
| Tid til «C.T.» / ¤ | = | . |
Sola i meridianen på sitt høyeste
| ¤ p.s.h. LMT | = | |
| rett lenge | = | |
| ¤ p.s.h. UTC | = | |
| Zone | = | |
| ¤ p.s.h. omb | = | |
| Kl. om bord | = | |
| Tid til ¤ p.s.h. | = | . |
Intervall til astronomiske observasjon ved sola for et skip underveis
Ih = $\frac{Tid}{1° + \frac{v \cdot \sin k}{900 \cdot \ cos b_a}}$
Ih = $\frac{t_{E}}{(15+\frac{\text{v}\cdot\sin k}{\left(60\cdot{\cos b}_{a} \right)})}$
Ih = $\frac{Tid}{1+{\frac{v\cdot\sin k}{900\cdot\cos b_a}}}$
| Ih | Tid til observasjon påv. plass | (timer) |
| tE | Lokal timevinkel øst i grader | (360° - t) |
| v | Skipets fart | (knop) |
| ba | Avfarende bredde |
Intervall til astronomiske observasjon ved stjerner for et skip underveis
Ih = $\frac{t_{E}}{(15°02'5+\frac{\text{v}\cdot\sin k}{\left(60\cdot{\cos b}_{a} \right)})}$
| Ih | Tid å seile til observasjon | (timer) |
Ukjent stjerne
sin d = sin b ⋅ sin h + cos b ⋅ cos h ⋅ cos pr
| d | Stjernens deklinasjon | (° og ‘) |
| b | Påværende bredde | (°og ‘) |
| h | Stjernens høyde | (° og ‘) |
| pr | Himmellegemets rettvisende peiling | (0o - 360o) |
Kap. 18 Posisjonsbestemmelser
Ved sola utenfor meridianen
(1)
| Posisjonsdata |
| Dato : |
| Kl. omb. : |
| sone : |
| Eb : |
(2)
| Ca. UTC og dato | Korrekt UTC* | |||||
| LT. omb. | = | Dato | Kr.v. | = | ||
| Zone | = | Kr.st. | = ± | |||
| Ca. UTC | = | Dato | UTC | = | Dato |
(3)
| Timevinkel | Deklinasjon | ||||||
| ¤ GHA t | = | ¤ deklinasjon | = | ||||
| rett. for t og s | = | + | (d = ) | = | ± | ||
| ¤ GHA d.g.ø. | = | ¤ dekl. d.g.ø. | = | ||||
| E/W lengde | = | ± | |||||
| ¤ LHA | = | ° | ‘ | ==> | tE | = | 360° - LHA |
(4) Beregnet høyde og rettvisende peiling
sin h = sin b ⋅ sin d + cos b ⋅ cos d ⋅ cos t
cos p = $\frac{(\sin{d-\sin{\text{b}\cdot\sin{h)}}}}{\cos{\text{b}\cdot\cos h}}$
| h | Beregnet høyde | (° og ‘) |
| b | Påværende bredde | (° og ‘) |
| d | Deklinasjon | (° og ‘) |
| t | Lokal timevinkel vest (LHA) | (° og ‘) |
| Az | Rettvisende peiling regnes fra nord, både på N og S bredde (0°-180°) |
(5)
| Høydeforskjell og retning | ||||
| ¤ avleste høyde | = | ° | ' | |
| Indeksfeil | = | ± | ° | ' |
| DIP (m) | = | − | ° | |
| ¤ tils. høyde | = | ° | ' | |
| Corr. UL/LL | = | ° | ' | |
| ¤ obs. høyde | = | ° | ' | |
| ¤ ber. høyde | = | − | ° | ' |
| Høydeforskjell | = | ± | ° | ' |
| DIP | Kimmingdalingen øyehøyde (over havflaten) |
| Corr | Samlet rettelse for Strålebrytning, Halvdiameter og Parallakse. |
| + | Solas underrand (Lower Limb) |
| - | Solas overrand (Upper Limb) |
(6)
| Konstruksjon av liten plotteskisse |
b' = 1 cm
l' = 1 cm ⋅ cos b
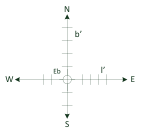
| Eb | Etter bestikk |
| b | bestikkbredde |
Ved sola i meridianen
(1) Posisjonsdata
| Dato : | |
| Kl. omb. : | |
| sone : | |
| Eb : |
*(2) *
| Ca. UTC og dato | Korrekt UTC* | ||||||
| LT omb. | = | (Dato) | Kr.v. | = | |||
| Zone | = | . | Kr.st. | = | ± . | ||
| Ca. UTC | = | . | (Dato) | UTC | = | . | (Dato) |
(3)
| Timevinkel | Deklinasjon | ||||
| LHA er 000° når sola er i øvremeridianen (+1) | deklinasjon | = | ° | ' | |
| (d = ) | = | ± | ° | ' | |
| LHA er 180° når sola er i nedremeridianen (-1) | dekl. d.g.ø. | = | ° | ' |
(4) Beregnet høyde og rettvisende peiling
sin h = sin b ⋅ sin d + cos b ⋅ cos d ⋅ ± 1
| p | = 180° eller 000° |
(5) Høydeforskjell og retning
| avleste høyde | = | ° | ' | |
| Indeksfeil | = | ± | ° | ' |
| DIP ( m) | = | - | ° | ' |
| tils. høyde | = | ° | ' | |
| Corr. UL/LL | = | ± | ° | ' |
| obs. høyde | = | ° | ' | |
| ber. høyde | = | - | ° | ' |
| Høydeforskjell | = | ± | ° | ' |
| DIP | Kimmingdalingen øyehøyde (over havflaten) |
| Corr | Samlet rettelse for Strålebrytning, Halvdiameter og Parallakse. |
| + | Solas underrand (Lower Limb) |
| - | Solas overrand (Upper Limb) |
| Konstruksjon av liten plotteskisse |
b' = 1 cm
l' = 1 cm ⋅ cos b

| Eb | Etter bestikk |
| b | bestikkbredde |
Ved stjerner
(1) Posisjonsdata
| Dato : | |
| Kl. omb.: | |
| sone : | |
| Eb : |
(2)
| Ca. UTC og dato | Korrekt UTC | |||||
| LT omb. | = | Kr.v. | = | |||
| Zone | = | . | Kr.st. | = | ± | . |
| Ca. UTC | = | . | UTC | = | . |
(3)
| Timevinkel | Deklinasjon | |||||||
|---|---|---|---|---|---|---|---|---|
| √ GHA t | = | ° | ‘ | |||||
| rett for m og s | = | ± | ° | ‘ | ||||
| rett. for m og s | = | + | ° | ‘ | ||||
| √ GHA d.g.ø. | = | ° | ‘ | |||||
| * SHA | = | + | ° | ‘ | ==> * deklinasjon | = | ° | ‘ |
| * GHA | = | ° | ‘ | |||||
| E/W lengde | = | ± | ° | ‘ | ||||
| * LHA | = | ° | ‘ |
| √ GHA | Aries timevinkel |
(4) Beregnet høyde og rettvisende peiling
sin h = sin b ⋅ sin d + cos b ⋅ cos d ⋅ cos t
cos Az = $\frac{(\sin{d - \sin{\text{b} \cdot \sin{h)}}}}{\cos{\text{b} \cdot \cos h}}$
| h | Beregnet høyde | (° og ‘) |
| b | Påværende bredde | (° og ‘) |
| d | Deklinasjon | (° og ‘) |
| t | Lokal timevinkel vest (LHA) | (° og ‘) |
| Az | Rettvisende peiling regnes fra nord, både på N og S bredde (0°-180°) |
(5) Høydeforskjell og retning
| * avleste høyde | = | ° | ‘ | |
| Indeksfeil | = | ± | ° | ‘ |
| DIP (m) | = | − | ° | |
| * tils. høyde | = | ° | ‘ | |
| Corr. | = | ° | ‘ | |
| * obs. høyde | = | ° | ‘ | |
| * ber. høyde | = | − | ° | ‘ |
| Høydeforskjell | = | ± | ° | ‘ |
| DIP | Kimmingdalingen, øyehøyde (over havflaten) |
| corr. | Strålebrytning (trekkes fra) |
(6) Konstruksjon av liten plotteskisse
b' = 1 cm
l' = 1 cm ⋅ cos b

| Eb | Etter bestikk |
| b | bestikkbredde |
Ved Planeter
(1) Posisjonsdata
| Dato : | |
| Kl. om bord : | |
| Zone : | |
| Eb : |
(2)
| Ca. UTC | Korrekt UTC | |||||
| Kl. omb. | = | Kr.v. | = | |||
| Zone | = | Kr.st. | = | ± | ||
| Ca. UTC | = | UTC | = |
(3)
| Timevinkel | Deklinasjon | |||||||
| Planet GHA t | = | ° | ‘ | Decl | = | ° | ‘ | |
| rett. for m og s | = | + | ° | ‘ | (d = ) corn. | = | ° | ‘ |
| v korr. | = | ° | ‘ | Decl | = | ° | ‘ | |
| Planet GHA | = | + | ° | ‘ | ||||
| Planet LHA | = | ° | ‘ |
(4) Beregnet høyde og rettvisende peiling
sin h = sin b ⋅ sin d + cos b ⋅ cos d ⋅ cos t
cos Az = $\frac{(\sin{d-\sin{\text{b}\cdot\sin{h)}}}}{\cos{\text{b}\cdot\cos h}}$
| h | Beregnet høyde | (° og ‘) |
| b | Påværende bredde | (° og ‘) |
| d | Deklinasjon | (° og ‘) |
| t | Lokal timevinkel vest (LHA) | (° og ‘) |
| Az | Rettvisende peiling regnes fra nord, både på nord og sør bredde (0°-180°) |
(5) Høydeforskjell og retning
| Planet avl. hd | = | ° | ‘ | |
| Indexfeil | = | ± | ° | ‘ |
| DIP | = | – | ° | ‘ |
| \Planet tils hd | = | ° | ‘ | |
| Corr. (LHA) | = | ° | ‘ | |
| Planet obs. hd | = | ° | ‘ | |
| Planet ber. hd | = | – | ° | ‘ |
| Høydeforskjell | = | ± | ° | ‘ |
| DIP | Kimmingdalingen, øyehøyde (over havflaten) |
| Corr. | Strålebrytning (trekkes fra) |
(6)
b' = 1 cm
l' = 1 cm ⋅ cos b

| Eb | Etter bestikk |
| b | bestikkbredde |
Ved Polaris
(1)
| Dato : | |
| Kl. om bord : | |
| sone : | |
| Eb : |
(2)
| Ca. UTC | Korrekt UTC | |||||
| Kl. omb. | = | Kr.v. | = | |||
| Zone | = | Kr.st. | = | ± | ||
| Ca. UTC | = | UTC | = |
(3) Lokal timevinkel Aries
| √ GHA t | = | ° | ' | |
| rett. for m og s | = | + | ° | ' |
| √ GHA d.g.ø. | = | ° | ' | |
| E/W lengde | = | ± | ° | ' |
| √ LHA | = | ° | ' |
| √ GHA | Aries timevinkel Greenwich |
4) Observert bredde
| | | | | |
| :-- | :-- | :-- | :-- | :-- | :-- |
| ★ avleste høyde | = || ° | '
| Indeksfeil | = | | ± | ° | '
| [DIP ( m) | = | − | ° | '
| ★ rette høyde | = | | °| '
| a0 (√ LHA) | = | + | '
| a1 (bredde)| =| + | '
| a2 (mnd) | = | + | '
| ∑ | = | | ° | '
| | | - 1°
|Obs. bredde| =| |° |' |
| DIP | Kimmingdalingen, øyehøyde (over havflaten) |
| Rettelsene tas ut i samme kolonne som LHA Aries. |
Kap. 19 SOLA I SANNN OPP- OG NEDGANG
Ved å ta utgangspunkt i solas meridianpassasje og beregne halv dagbue, kan solas sanne opp- og nedgang beregnes. Halv dagbue er vinkelen fra sola er i meridianen til sola er i den sanne horisont.
Halv dagbue
cos t° = ± tan b ⋅ tan d
NB! Brukes ikke fortegn på bredde og deklinasjon.
+ når bredde og deklinasjon har motsatt navn
- når bredde og deklinasjon har samme navn
Når bredde og deklinasjon samme navn:
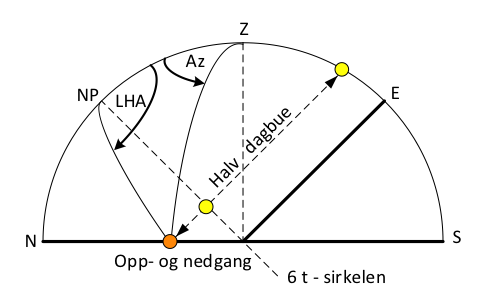
| Az | Blir mindre enn 90 |
| LHA | Blir større enn 90 |
| Halv dagbue | Mer enn 6 timer |
cos t° = - tan b ⋅ tan d
tt = t / 15°
| t° | Halv dagbue | (° og ') |
| b | Påværende bredde | |
| d | Solas deklinasjon | |
| tt | Halv dagbue | (t og m) |
Når bredde og deklinasjon motsatt navn:

| Az | Blir større enn 90_ |
| LHA | Blir mindre enn 90 |
| Halv | dagbue Mindre enn 6 timer |
cos t° = + tan b ⋅ tan d
tt = t° / 15°
| t° | Halv dagbue | (° og ') |
| b | Påværende bredde | |
| d | Solas deklinasjon | |
| tt | Halv dagbue | (t og m) |
Sola i sann opp-nedgang
| ◉ i meridianen LMT | = | . | |||
| større/mindre kl Gr. | = | ± | . | ||
| ◉ i mer. UTC | = | . | |||
| sone | = | ± | . | ||
| ◉ i meridianen LT | = | . | |||
| tt | = | ± | . | ||
| ◉ i sann opp-/nedg. LT | = | . |
Kap. 20 DEVIASJONSUNDERSØKELSE
Tidasimut (ved deviasjonsundersøkelser)
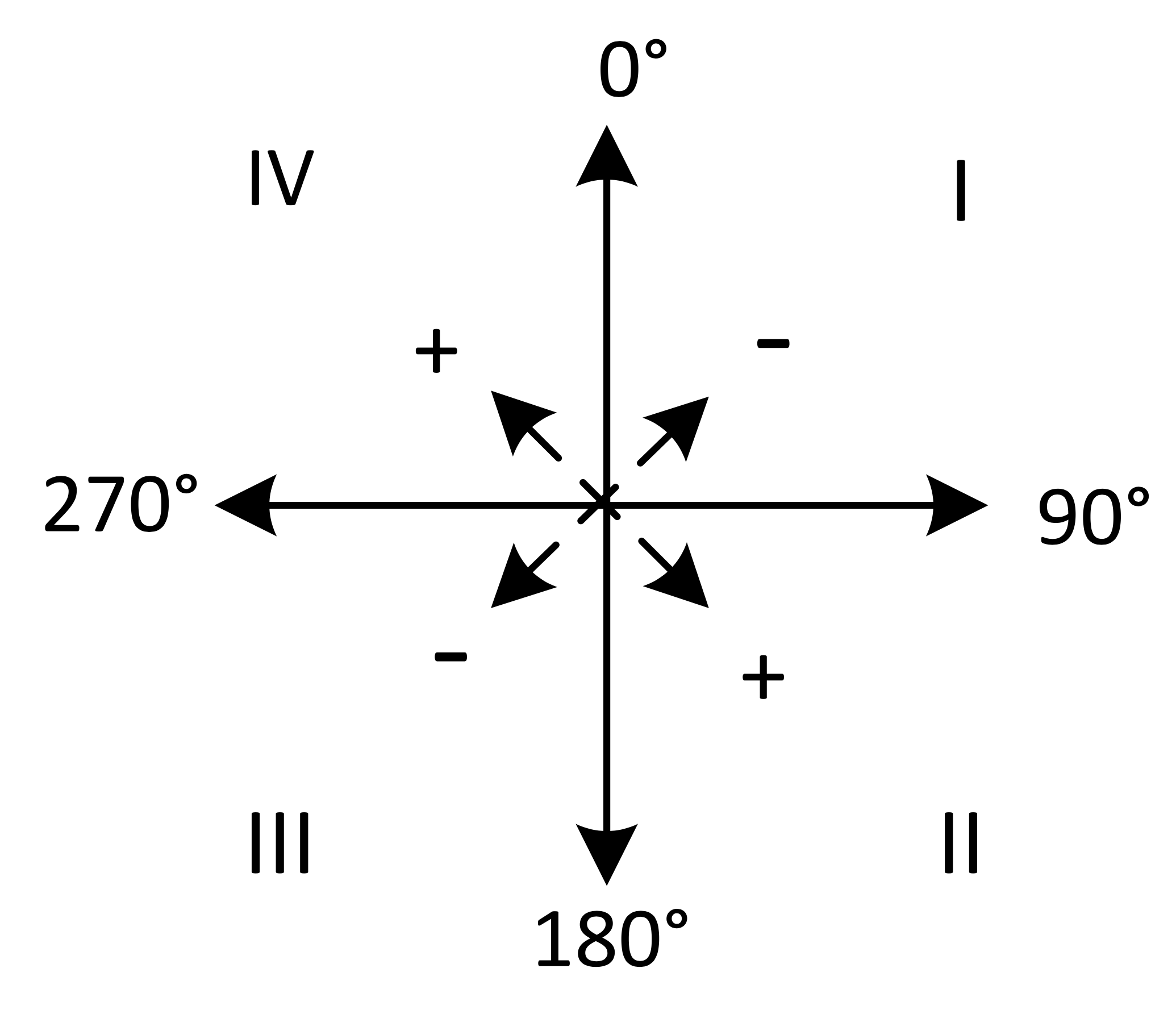
tan pk = $\frac{\sin t}{(\tan{{d}\cdot\cos{b – \sin{{b}\cdot\cos{t)}}}}}$
(0° - 90°)
| pk | Kvadrantpeiling | (0° – 90°) |
| t | Lokal timevinkel | (° og ‘) |
| d | Deklinasjon | (° og ‘) |
| b | Påværende bredde | (° og ‘) |
| h | Himmellegemets høyde | (° og ‘) |
Rettvisende peiling finnes etter følgende fortegns-regel, som er lik for nord og sør bredde.
I forbindelse med høydeobservasjon
cos Az = $\frac{(\sin{d\ - \ \sin{\text{b} \cdot \sin{h)}}}}{\cos{\text{b} \cdot \cos h}}$
| Az | Rettvisende peiling regnes fra nord, både på nord og sør bredde (0°-180°) |
Asimut i sann opp- og nedgang
cos p = $\frac{\sin{d}}{\cos{b}}$
Særtilfelle av høydeasimut når h = 0o
| p | Rettvisende peiling regnes fra nord, både på nord og sør bredde | (0° – 180°) |
| d | Deklinasjon | (° og ‘) |
| b | Påværende bredde | (° og ‘) |
| NB! | Bør ikke brukes på «høye» bredder uten å beregne halv dagbue og tidspunkt for for sola i sann oppgang. |
Feilvisning og deviasjon
| Rettvisende peiling | = | ° | |
| Gyro peiling | = | - | ° |
| Feilvisning | = | ± | ° |
| Gyrokurs | = | ° | |
| feilvisning | = | ± | ° |
| Rettvisende kurs | = | ° | |
| misvisning | = | ± | ° |
| Magnetisk kurs | = | ° | |
| Kompasskurs | = | - | ° |
| deviasjon | = | ± | ° |
Kap. 21 RUTEPLANLEGGING
Ruteplanlegging deles i 4 stadier
| 1. Appraisal | (Vurdering / forventning) |
| 2. Planning | (Planlegging) |
| 3. Execution of the plan | (Gjennomføring) |
| 4. Monitoring progress | (Overvåkning/kontroll) |
Målsetning
• Seilasen skal foretas på den hurtigste måte
• Seilasen skal foretas på den sikreste måte
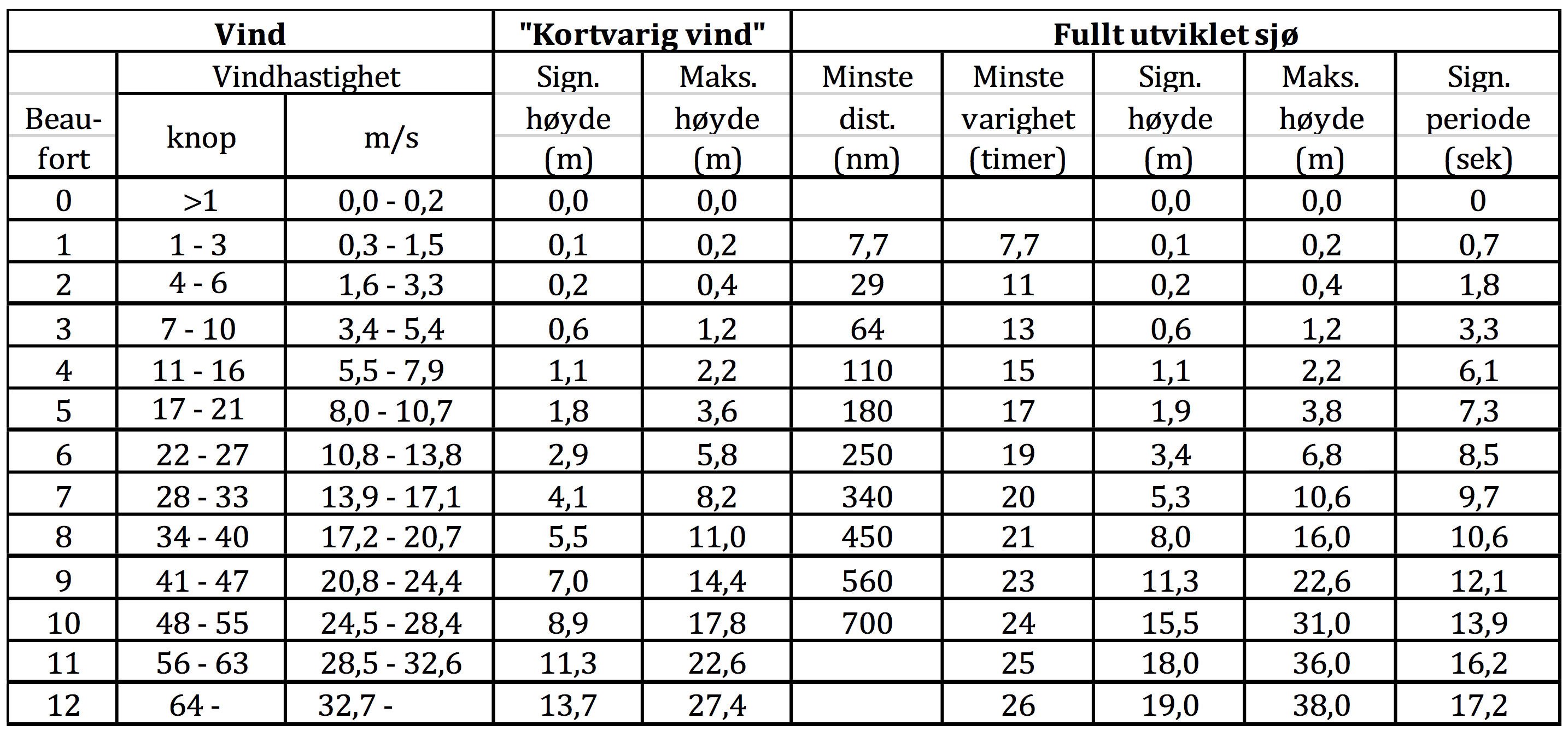
Vindstyrke
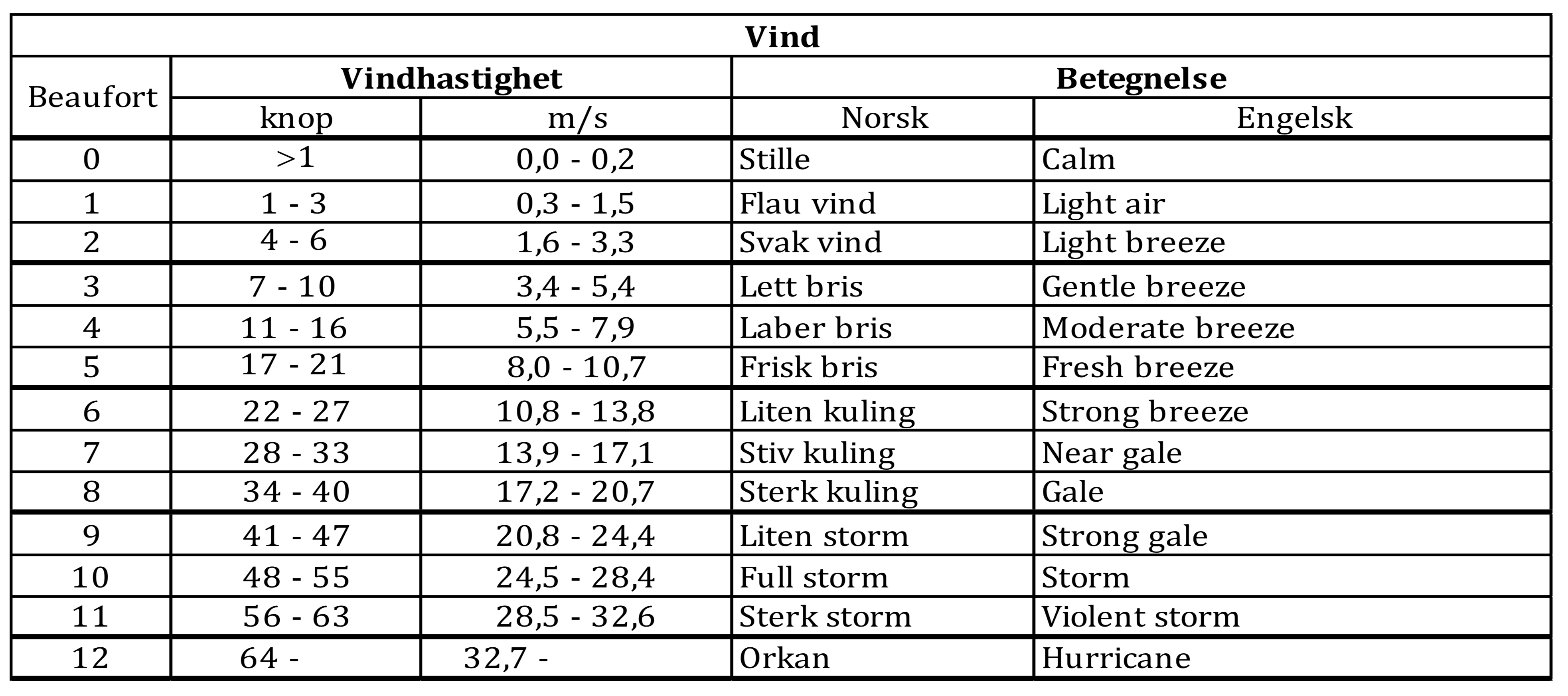
Vindstyrke og bølgehøyde
På våre bredder vil større vindhastigheter som regel oppstå pga. lavtrykk som kommer inn fra vest.
Passerer relativt fort, og ved kraftig vind er det sjelden at det blir fullt utviklet sjø.
Imidlertid vil det oppstå irregulær sjø med varierende bølgehøyde.
Den høyeste bølge man kan vente seg er ca. 2 ganger signifikant bølgehøyde.